57.Понятие о силовом поле и потенциальной энергии

СИЛОВОЕ ПОЛЕ

- часть пространства (ограниченная или неограниченная),в каждой точке к-рой на помещённую туда материальную частицу действуетопределённая по численной величине и направлению сила, зависящая толькоот координат х, у, z этой точки. Такое С. п. наз. стационарным;если сила поля зависит и от времени, то С. п. наз. нестационарным; еслисила во всех точках С. п. имеет одно и то же значение, т. е. не зависитни от координат, ни от времени, С. п. наз. однородным.

Стационарное С. п. может быть задано ур-ниями

где F_x, F_y, F_z - проекции силыполя F.

Если существует такая ф-ция U(x, у,z), называемая силовой ф-цией, <что элементарная работа сил поля равна полному дифференциалу этой ф-ции, <то С. п. наз. потенциальным. В этом случае С. п. задаётся одной ф-цией U(x,у, z), а сила F может быть определена через эту ф-цию равенствами:

или . Условиесуществования силовой ф-ции для данного С. п. состоит в том, что

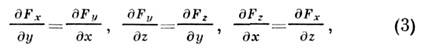
или . При перемещении в потенциальном С. п. из точки M₁(x₁,y₁, z₁ )в точку М ₂ (х ₂,у ₂,z₂) работа сил поля определяется равенством и не зависит от вида траектории, по к-рои перемещается точка приложениясилы.

Поверхности U(x, у,z) = const, на к-рых ф-ция сохраняет пост. <значение, наз. поверхностями уровня. Сила в каждой точке поля направленапо нормали к проходящей через эту точку поверхности уровня; при перемещениивдоль поверхности уровня работа сил поля равна нулю.

Примеры потенциального С. п.: однородное поле тяжести, для к-рого U= -mgz, где т - масса движущейся в поле частицы, g - ускорениесилы тяжести (ось z направлена вертикально вверх); ньютоново полетяготения, для к-рого U = km/r, где r = - расстояние от центра притяжения, k - постоянный для данного поля коэффициент. <Вместо силовой ф-ции в качестве характеристики потенциального С. п. можноввести потенциальную энергию П, связанную с U зависимостью П(х, <у, z)= = -U(x, у,z). Изучение движения частицы в потенциальномС. п. (при отсутствии других сил) существенно упрощается, т. к. в этомслучае имеет место закон сохранения механич. энергии, позволяющий установитьпрямую зависимость между скоростью частицы и её положением в С. п. с. <м. Тарг. СИЛОВЫЕ ЛИНИИ - семейство кривых, характеризующих пространственноераспределение векторного поля сил; направление вектора поля в каждой точкесовпадает с касательной к С. л. Т. о., ур-ния С. л. произвольного векторногополя А (х, у,z) записываются в виде:

Плотность С. л. характеризует интенсивность (величину) силового поля. <Область пространства, ограниченная С. л., пересекающими к.-л. замкнутуюкривую, наз. силовой трубкой. С. л. вихревого поля замкнуты. С. л. потенциальногополя начинаются на источниках поля и заканчиваются на его стоках (источникахотрицат. знака).

Понятие С. л. введено М. Фарадеем при исследовании магнетизма, а затемполучило дальнейшее развитие в работах Дж. К. Максвелла по электромагнетизму. <Согласно представлениям Фарадея и Максвелла, в пространстве, пронизываемомС. л. электрич. и магн. полей, существуют механич. напряжения, соответствующиенатяжению вдоль С. л. и давлению поперёк них. Математически эта концепциявыражена в Максвелла тензоре натяжений эл.-магн. поля.

Наряду с использованием понятия С. л. чаще говорят просто о линиях поля:напряжённости электрич. поля Е, индукции магн. поля В и т. <п., не делая спец. акцента на отношение этих нолей к силам.

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ

- часть энергии ме-ханич. системы, находящейся в нек-ром силовом поле, зависящая от положения точек (частиц) системы в этом поле, т. е. от их координатили от обобщённых

координат системы Численно п. э. системы в данном её положении равна той работе, к-рую произведут действующие на систему силы поля при перемещении системы из этого положения в то, где П. э. условно принимается равной нулю (нулевое положение). Из определения следует, что понятие П. э. имеет место только для системы, находящейся в потенциальном силовом поле, в к-ром работа действующих на систему сил поля зависит только от начального и конечного положений системы и не зависит от закона движения точек системы, в частности от вида их траекторий. Напр., для механич. системы, находящейся в однородном поле тяжести, если ось направлена вертикально вверх, П. э. где т- масса системы, g- ускорение силы тяжести, - координата центра масс (нулевое положение = 0); для двух частиц с массами притягивающихся друг к другу по всемирного тяготения закону, где G- гравитационная постоянная, - расстояние между частицами (нулевое положение ). Аналогично определяется П. э. двух точечных зарядов и

С силовой ф-цией П. э. связана соотношением

Следовательно, П. э. и определяет данное потенциальное силовое поле. Значение силы в любой точке поля равно градиенту П. э., взятому со знаком минус; поверхности П = const являются поверхностями уровня. Работа сил поля при перемещении системы из положения, где П. э. равна в положение, где П. э. равна П ₂, будет С. М. Таре.

Для системы материальных точек полная энергия (Гамильтона функция )есть сумма кинетической и П. э. Вообще говоря, это разбиение неоднозначно, но обычно полагают, что П. э.- это часть суммы, зависящая только от координат. Для систем, не имеющих не-посредств. механич. аналога, П. э.- это слагаемое в выражении для полной энергии системы, зависящее только от обобщённых координат. Напр., для плотности энергии эл.-магн. поля в вакууме член не зависящий от обобщённых импульсов, играет роль П. э.

В квантовой теории ф-ция Гамильтона становится оператором Гамильтона ( гамильтонианом). Его часть

зависящая только от координат (операторов) интерпретируется как оператор П. э. Реализация оператора П. э. зависит от выбора представления; в координатном представлении - это просто оператор умножения на числовую ф-цию U(q). В др. представлениях вид оператора П. э. может быть более сложным: напр., в импульсном представлении - это дифференц. оператор В. П. Павлов,

58.Законы сохранения в динамике

59.Динамика тела. Основные понятия. Моменты инерции тел

60.Дифферециальные уравнения поступательного, вращательного и плоского движения

Динамика твердого тела

Дифференциальные ур-ния поступательного движения твердого тела:  и т.д. – проекция внешней силы. Все точки тела движутся так же, как и его центр масс С. Для осуществления поступательного движения необходимо, чтобы главный момент всех внешних сил относительно центра масс был равен 0:  =0.

Дифф-ные ур-ния вращения твердого тела вокруг неподвижной оси:  ,

J_z – момент инерции тела относительно оси вращения z, – момент внешних сил относительно оси вращения (вращающий момент).   _,    – угловое ускорение, чем больше момент инерции при данном _, тем меньше ускорение, т.е момент инерции при вращательном движении является аналогом массы при поступательном. Зная _, можно найти закон вращения тела =f(t), и, наоборот, зная =f(t), можно найти момент. Частные случаи: 1) если = 0, то  = const – тело вращается равномерно; 2) = const, то  = const – вращение равнопеременное. Уравнение аналогичное дифф-ному уравнению прямолинейного движения точки .

Физический маятник – твердое тело, совершающее колебания вокруг неподвижной горизонтальной оси под действием силы тяжести. Ур-ние вращательного движения:

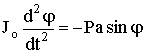
, обозначая 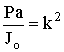, получаем дифф-ное уравнение колебаний маятника: , k – частота колебаний маятника. Рассматривая малые колебания, можно считать sin  , тогда  – дифф-ное уравнение гармонических колебаний. Решение этого уравнения:  = С₁coskt + C₂ sinkt или   = sin(kt + ),   – амплитуда колебаний маятника,  – начальная фаза колебаний. Период малых колебаний физического маятника Т= 2/k = 2 . Для малых колебаний маятника период не зависит от угла начального отклонения, этот результат является приближенным. Для математического маятника (материальной точки, подвешенной на нерастяжимой нити и движущейся под действием силы тяжести) имеем дифф. уравнения движения:

, L – длина нити. Если L= , то математический маятник будет двигаться так же, как и физический (период колебаний совпадает). Величина L назыв-ся приведенной длиной физического маятника. Точка  К, отстоящая от оси подвеса на расстоянии ОК=L, назыв-ся центром качаний физич. маятника. Если ось подвеса взять в точке К, то точка О будет центром качаний и наоборот – свойство взаимности. Расстояние ОК всегда >ОС, т.е. центр качаний всегда расположен ниже центра масс

Динамика плоского движения твердого тела

Положение тела определяется положением полюса и углом поворота тела вокруг полюса. Дифф-ные уравнения плоского движения тв. тела:

;   ;   ,   С – центр масс тела, J_C – момент инерции тела относительно оси, перпендикулярной плоскости движения тела и проходящей через его центр масс.