8) Методы эквивалентных преобразований ( сущность и последовательность расчета).

Применяется для расчета цепей с одним источником ЭДС. Заключается в том что цепь или отдельные её участки заменяются более простыми по структуре участками цепи, при этом токи и напряжения не преобразованной части не должны изменится.

О бозначим узлы в схеме

З аменяем два параллельных включ. Сопротивлений R₄ и R₅ эквивалентным сопротивлением R₄₅. _{,и так далее , , ,}

_{, , Проверка.}

9)Метод наложения (сущность и последовательность расчета)

О н основан на принцепе наложения: Ток какой либо ветви сложной электрической цепи равен алгебраической сумме часных токов вызванных каждым действующим в цепи источником электрической энергии в отдельности.

Исключаем источник Е₃ из схемы закоротив его и оставив внутреннее сопротивление r₀₃ получаем.

_{. Аналогично отключаем Е1 источник и определяем частные токи}

н аходим _{токи в ветвях .}

10)Законы Киргофа и их применение прирасчете электрических цепей

1-й закон ( для узла) :

Алгебраическая сумма токов сходящихся в одном узле равна 0:

За положительный ток – ток идущий от узла, за отрицательный – ток к узлу.

Сумма входящих в узел тока равняется сумме выходящих из узла токов.

А)

Б)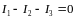

2-й закон (для контура) :

Сумма ЭДС какого либо замкнутого контура цепи равна алгебраической сумме падений напряжений в нем. Произвольно выбирается направление обхода контура. Со знаком «+» записываются те ЭДС и потери напряжений направления которых совпадают с направлением обхода контура .

Для левого контура:

Для правого контура:

вверх

11) Метод контурных токов ( сущность и последовательность расчета)

В основе метода лежит два предположения:

- в каждом контуре протекают независимые друг от друга токи называемые контурными, а ток каждой ветви равен алгебраической сумме контурных токов замыкающихся через эту ветвь.

Для контурных токов состовляется система ур-й по 2-му закону Киргофа.

Находим токи в ветвях.

Токи ветвей равны алгебраическим суммам контурных токов: если направление контурного тока совпадает с направлением тока цепи, то он записывается со знаком «+», а если не совподает то со знаком «-».

12. Метод узловых потенциалов (сущность и последовательность расчета).

Применяется для расчёта схем, у которых число узлов меньше числа независимых контуров. По этому методу составляется система уравнений, из которых можно определить потенциалы всех узлов схемы. А затем по известным разностям потенциалов определяются токи в ветвях.

Порядок расчёта:

1. выбирается условно положительное направление токов в ветвях;

2. принимается равным нулю потенциал одного из узлов;

3. составляется система из n уравнений вида:

G11φ1 - G12 φ2 - … - G1n φn = I11

-G21 φ1 + G22 φ2 - … - G2n φn = I22

………………………………………..

-Gn1 φ1 – Gn2 φ2 - … + Gnn φn = Inn

φ1 – φn – неизвестные потенциалы узлов;

Gmm – собственная проводимость узла m, равная суммарной проводимости ветвей, присоединённых к узлу m;

Gim = Gmi – межузловая проводимость, равная сумме проводимостей ветвей, включённых между узлами i и m;

Ii – узловой ток i-го узла, равный алгебраической сумме токов источника тока и произведений ЭДС источников на проводимость ветвей EiGi, присоединённых к рассматриваемому узлу, с «+» берутся токи и ЭДС, направленные к узлу;

4. решаем систему относительно потенциалов;

5. по закону Ома находим токи.