3.3.4. Розширення можливостей переходів під час моделювання

Переходи — це активні елементи мережі, які можуть спрацьовувати паралельно. Чи може перехід спрацьовувати паралельно, чи буде він спрацьовувати раніше ніж інші переходи — це повинно бути точно вказано у визначенні переходу під час моделювання. Порядок спрацьовування переходів визначає програма керування моделюванням. Щоб відтворити динаміку роботи системи, котра моделюється, переходи повинні спрацьовувати у відповідні моменти модельного часу.

Перехід може збуджуватися тільки тоді, коли виконано правила збудження. Для цього програма керування моделюванням відшукує маркери у вхідних вузлах кожного переходу, щоб перевірити вимоги виконання правил, визначених вхідними дугами. Якщо необхідна сукупність маркерів у вхідних вузлах переходу знайдена, він збуджується. Перехід спрацьовує тоді, коли виконуються всі чотири умови:

• пропускну здатність паралельності все ще не вичерпано (тобто, як часто залежний від часу перехід може спрацьовувати паралельно самому собі);

• вхідні вузли переходу містять достатню кількість маркерів з необхідними атрибутами, які відповідають виразам вхідних дуг;

• можуть бути виконані логічні умови, сформульовані для атрибутів маркерів вузлів;

• пропускна ємність вихідних вузлів цього переходу така, що вони здатні включити таку кількість маркерів, яка може бути задана числами пропускної здатності вихідних дуг, тобто числами, які визначають кількість маркерів, що потраплять у вихідні вузли.

Потім за допомогою програми моделювання перевіряються маркери у вхідних вузлах, які знищуються в поточний момент модельного часу (для вхідних дуг може бути заданий більш пізній час знищення маркерів), і маркери, що будуть створені для вихідних вузлів, генеруються після того, як закінчиться час переходу (для вихідних дуг може установлюватися час на дузі відносно часу переходу).

Розглянемо мережу Петрі, зображену на рис. 3.17 (чорні маркери позначено символом #). Під час перегляду сукупності маркерів у лівій частині мережі за допомогою програми керування моделюванням перевіряється правило збудження переходу Т1. Перехід може спрацювати, вилучаючи три чорних маркери з вхідного вузла Р1, генеруючи один чорний маркер у вихідному вузлі Р2 і п'ять чорних маркерів у вихідному вузлі Р3. Наступна сукупність маркерів не дає змогу переходу Т1 спрацювати знову, тому що вузол Р1 повинен мати принаймні три чорних маркери. Така сукупність маркерів може виникнути, наприклад, коли збуджується перехід, для якого вузол Р1 є вихідним вузлом.

Рис. 3.17. Ілюстрація до правила спрацювання переходів

Слід зробити одне попередження щодо конструкцій циклу. Відповідно до вищезгаданого правила перехід Т1 на рис. 3.18 не буде збудженим, якщо пропускна здатність вузла Р1 дорівнює одиниці. Така пропускна здатність недостатня для передавання маркера, тому що у вузлі Р1 уже є інший маркер. Однак цей маркер знищується вхідною дугою на початку спрацювання так, щоб точно в цей же момент часу пропускна здатність вузла була б достатньою для прийому іншого маркера. Інтуїтивне припущення, що перехід Т1 міг би спрацьовувати, буде дійсним, якщо вхідна дуга перевіряється за допомогою програми керування моделюванням раніше, ніж вихідна.

У пакетах моделювання мереж Петрі це так і реалізується. Принцип циклу також працює, коли вхідні й вихідні дуги мають різні значення часу збудження, і час збудження вхідної дуги менший, ніж час збудження вихідної дуги, або дорівнює йому. Бажано уникати конструкцій циклу із залежними від часу дугами.

Спрацювання переходу зазвичай приводить до того, що у вихідних вузлах утворюється нова сукупність маркерів. Таким способом може бути представлено потік даних. Щоб потік даних міг бути випущеним переходом, його слід обробити і представити за допомогою опису переходу.

Переходи, які спрацьовують у модельному часі

Для того щоб моделювати динамічні системи, потрібно мати можливість пов'язати моменти спрацювання переходів з модельним часом (рис. 3.19). Вирізняють переходи кількох типів — миттєвий, експоненціальний і детермінований.

Миттєвий перехід не пов'язаний з моментом часу, і його перемикання здійснюється так, як було описано вище. Такий перехід відображається зазвичай на схемі мережі Петрі як штрих або вузький прямокутник. Якщо час спрацьовування переходу розподілений за експоненціальним законом, то такий перехід зображують незафарбованим прямокутником, а якщо час спрацьовування переходу детермінований – зафарбованим прямокутником. Мережу Петрі, в якій час спрацьовування переходів задано через імовірнісний розподіл, називають стохастичною мережею Петрі.

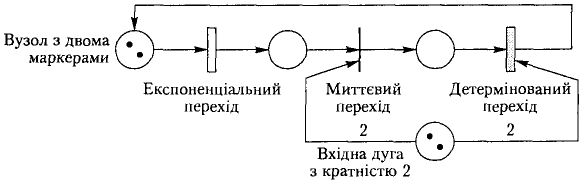
Рис. 3.19. Мережа Петрі з різними типами переходів

Час спрацьовування переходу може бути фіксованим або розрахованим. Він залежить від масштабу часу, прийнятому в моделі, і такту часу, який визначає розробник моделі. Модельний час просувається з деяким фіксованим значенням такту часу, наприклад кожну секунду. Похибки округлення часу не впливають на точність, якщо час моделювання задається як цілочисловий тип даних.

Детерміноване значення часу спрацьовування може бути безпосередньо призначене атрибуту переходу, тоді як довільне значення часу має бути визначене (точніше, розраховане) у процесі моделювання, тому що воно може залежати від значень маркера. Таким чином, нове довільне значення часу для переходу встановлюється для кожного такту модельного часу, як і для спрацювання переходу.

Фрагмент мережі Петрі, зображений на рис. 3.20, ілюструє окремі можливості спрацювання переходів. Переходи Т1 і Т2 починають збуджуватись у момент часу 0. Після моделювання протягом 10 с перехід Т1 генерує маркер, а перехід T2 генерує маркер після моделювання протягом 20 с. Після цього жоден з переходів не може збуджуватися знову, тому що вузол Р1 більше не забезпечує достатньої кількості маркерів.

Більшість систем моделювання підтримує різні закони розподілу часу для спрацювання переходів. Наприклад, система POSES ++ підтримує рівномірний, нормальний, логарифмічний розподіли, гамма-розподіл, показовий і пуассонівський розподіли. У разі необхідності інші функції розподілу може бути додано за допомогою мови С.

Слід зауважити, що визначення часу спрацьовування переходу може бути пов'язане з вузлом, тобто вузол Р може бути пов'язаний з часом . У цьому випадку, якщо маркер з'явиться у вузлі Р у час t, то перехід, для якого Р є вхідним вузлом, може спрацювати тільки в час t + .

Паралельність спрацьовування переходів

За достатньої кількості маркерів у вхідних вузлах переходи можуть спрацьовувати паралельно кілька разів, доки в них не вичерпаються маркери. Це дає змогу описувати досить складні реальні процеси і системи. Кількість спрацьовувань переходу задається значенням паралельності в системі, яка моделюється. Наприклад, стандартне значення паралельності в системі POSES ++ дорівнює 2³², тобто може змінюватись від 1 до 4 294 967 295, що є достатнім для досягнення практичних цілей.

Перехід Т1 (рис. 3.21) тричі спрацьовує одночасно, тому що обмеження паралельності не визначене. Якщо задати значення паралельності переходу 2, то він міг би спрацьовувати паралельно тільки двічі. Обмеження паралельності не впливає на переходи, для яких не вказаний час спрацьовування. Коли цей час визначено (наприклад, фіксований час 10 с), функціонування переходу відзначається в статистиці результатів моделювання, наприклад: «У час 0 два спрацьовування починаються одночасно і продовжуються 10 с». У модельний час 10 с починається третє спрацьовування і продовжується воно протягом 10 с (доки тривалість модельного часу не досягне 20 с).

Таких же функціональних можливостей можна досягти, якщо змінити структуру моделі. Для цього є маркери, що діють як ресурси (resources), і використовуються, щоб забезпечити максимальну кількість паралельного спрацьовування переходів (на рис. 3.22 два маркери у вузлі Р5 – це ресурси, наприклад пристрої для обслуговування).

Пріоритети переходів

Оскільки для спрацьовування переходу треба перевірити правила збудження, виникає ситуація, коли окремі переходи конкурують між собою за володіння маркерами. Доки не задані ніякі пріоритети, переходи, що конкурують, вирішують проблеми довільно, тобто генератор випадкових чисел з однаковою ймовірністю для всіх переходів визначає, який з них повинен перевірятися спочатку. Якщо для цього переходу виконується правило, то він збуджується раніше за тих, які могли б також збуджуватись.

Приклад конкуруючих переходів наведено на рис. 3.23.

Якщо, наприклад, потрібно, щоб переходи Т1 і ТЗ спрацьовували раніше, ніж переходи Т2 і Т4, необхідно встановити їх пріоритети. Стандартний пріоритет переходу в системі POSES ++ має значення 100. Максимально можливий пріоритет дорівнює 1. Усі інші пріоритети відповідно нижчі. Найнижчий можливий пріоритет 2³², тобто пріоритети можуть у системі POSES ++ приймати значення від 1 до 4 294 967 295. У будь-якому випадку програма керування моделюванням перевіряє всі переходи, що мають більш високий пріоритет, і вони спрацьовують раніше, ніж переходи з більш низьким пріоритетом. Якщо окремі переходи мають однаковий пріоритет, програма керування моделюванням вибирає один перехід довільно (відповідно до принципу рівномірного розподілу), і він збуджується.

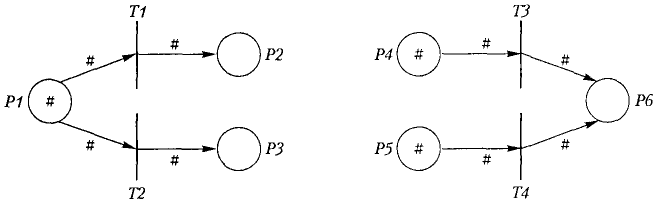
Рис. 3.23. Конкуруючі переходи

Приклад 3.4

Розглянемо, як можна використовувати розширені мережі Петрі для моделювання СМО. Нехай необхідно побудувати модель розімкнутої мережі СМО, в якій є два пристрої для обслуговування, до яких надходять вимоги кожні 30 хв. Час обслуговування першим одноканальним пристроєм рівномірно розподілений в інтервалі від 20 до 30 хв. Часові переходи можуть мати позначки, які вказують розподіли ймовірностей для їх тривалості.

Після обслуговування 80% вимог надходять до другого одноканального пристрою із середнім часом обслуговування 10 хв, розподіленим за експоненціальним законом, а 20% вимог уникають обслуговування другим пристроєм і залишають систему. На рис. 3.24 зображено мережу Петрі, яка моделює цю систему.

Рис. 3.24. Застосування мережі Петрі для моделювання СМО

Маркери використовуються для зображення вимог, ресурсів (пристроїв для обслуговування вимог) і перевірки стану пристроїв. Маркери-вимоги генеруються деяким процесом надходження вимог. Маркери-ресурси застосовуються для початкового маркування вузлів-ресурсів, які повинні використовувати маркери-вимоги. Маркери перевірки використовуються для задания будь-яких спеціальних умов, що можуть впливати на обслуговування вимог.

У моделі використовуються різні типи вузлів. Вузол Р1, який генерує вимоги, позначений як GEN, вузли Р5, Р7, що знищують вимоги, — як TERM. Вузол Р1 є місцем введення і виведення маркерів для часового переходу Т1, який збуджується кожні 30 хв. Таким чином, маркери-вимоги надходять кожні 30 хв до вузла Р2, який моделює чергу для першого одноканального пристрою.