3.2.2. Формалізоване зображення моделі за допомогою мережі Петрі

Один із найскладніших етапів створення моделі — це вибір методу її формалізації. Зазвичай існує кілька підходів до зображення моделі системи і мережі Петрі. Продемонструємо на прикладах, як перейти від змістовної постановки задачі до формальної моделі.

Приклад 3.1

Покажемо, як за допомогою мережі Петрі можна синхронізувати кілька асинхронних обчислювальних процесів, що виконуються в пам'яті комп'ютера. Розглянемо роботу комп'ютерної системи, в якій два обчислювальні процеси П₁ і П₂ намагаються одночасно записати дані в область пам'яті (П₁) і зчитати з неї дані (П₂). Проблема, яку потрібно вирішити — синхронізація доступу процесів до пам'яті. Щоб запобігти суперечності, необхідно заборонити одночасний доступ процесів до одної і тої ж області пам'яті. Це означає, що активним може бути тільки один процес, який виконує операцію доступу до пам'яті.

Для формалізації модельованої системи скористаємося семафором, який буде розділяти доступ до області пам'яті. Побудуємо просту мережу Петрі (рис. 3.9), яку можна буде використати для синхронізації цих процесів, і розглянемо її роботу.

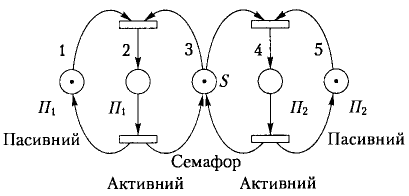
Рис. 3.9. Застосування мережі Петрі для синхронізації асинхронних процесів

Кожний обчислювальний процес може перебувати в одному з двох станів: активному або пасивному, які відповідно позначені двома вузлами. Розташування маркерів у мережі, зображеній на рис. 3.7, показує, що в даний момент обидва процеси знаходяться в пасивному стані. Кожний процес може змінити свій стан за допомогою спрацювання переходу. Зміна стану мережі залежить від вузла семафора — S. Розмітка вихідного стану мережі М = [1, 0, 1, 0, 1]. Якщо один процес, наприклад П₁, намагається змінити свій стан на активний (записати дані), то він збуджує свій перехід і змінює розмітку мережі на М = [0, 1, 0, 0, 1]. Таким чином, збудження переходу процесу П₂ (зчитування даних з тієї ж області) не станеться доти, доки процес П₁, не перейде в пасивний стан і розмітка мережі знову не зміниться на М = [1, 0, 1, 0, 1].

Приклад 3.2

Покажемо, як за допомогою мереж Петрі можна описати роботу світлофора, що керує дорожнім рухом. Модель світлофора можна використовувати для моделювання систем керування рухом транспорту. Ця модель має відтворювати зміну станів світлофора: зелене світло, жовте світло, червоне світло і червоно-жовте світло. Для формалізації модельованої системи скористаємося простою мережею Петрі, вузли якої будуть визначати стани світлофора, а положення чорного маркера — поточний його стан (рис. 3.10).

Рис. 3.10. Модель функціонування світлофора

На рис. 3.10 зображено модель роботи світлофора, стан якої відповідає ситуації, коли горить зелене світло (цей стан позначено маркером). Динаміку роботи світлофора, тобто зміну його світла і відповідно положення маркера в мережі Петрі, можна відтворити за допомогою переходів, для яких мають виконуватись правила збудження та спрацьовування. У мережі на рис. 3.10 збудженим є тільки перехід, який відповідає зміні зеленого світла на жовте. У разі спрацювання переходу маркер із зеленого вузла переміщується в жовтий. Зміна положення маркера приводить до нового стану моделі, що відповідає ситуації, коли горить жовте світло. Із цього стану можливий перехід тільки до стану, який відповідає ситуації, коли горить червоне світло. Таким чином, ця модель описує всі стани світлофора, які змінюються в певній послідовності.

Для формалізації моделі світлофора можна скористатися й іншим підходом, коли всі стани світлофора та переходи можна зобразити графічно за допомогою скінченного автомата. Скінченний автомат — це граф станів (вершин) і переходів (дуг). Стан такого автомата позначається маркером в одній із його вершин. Модель функціонування світлофора у вигляді скінченного автомата зображено на рис. 3.11.

Поточний стан моделі (рис. 3.11) позначається тільки одним маркером (слід звернути увагу, що в мережі Петрі для позначення стану моделі світлофора, в якому одночасно горить червоне і жовте світло, використовувалось два маркери). Множину можливих станів такої моделі можна розширити, наприклад ввести стан світлофора, коли горить зелене і жовте світло. Кількість необхідних маркерів моделі в цьому разі не зміниться, але модель стане більш складною — з'являться ще один вузол і перехід. Таким чином, виникають запитання: чи потрібно всі стани моделі відображати окремими вузлами; чи можна позначати поточний стан моделі за допомогою маркерів різного кольору, як це зроблено на рис. 3.12. Таким чином, можна перейти ще до одного підходу до формалізації моделі світлофора.

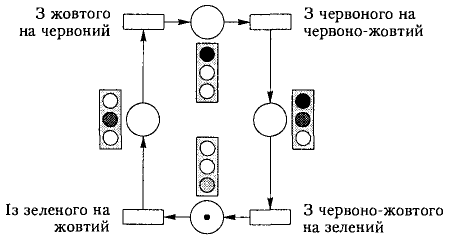
Рис. 3.11. Модель функціонування світлофора у вигляді скінченного автомата

Рис. 3.12. Модель із загальним станом світлофора «горить якесь світло»

Такий підхід передбачає, що стани світлофора в мережі Петрі, які зображувались раніше кількома різними вузлами, зображуються лише одним вузлом, в якому знаходиться маркер відповідного кольору (зелений, жовтий, червоний і червоно-жовтий). На рис. 3.12 зображено мережу Петрі, поточний стан якої визначає зелений маркер, що знаходиться в її вузлі. Стан мережі змінюється тільки після спрацювання переходу від зеленого світла до жовтого. Для збудження цього переходу повинні виконуватись обидві умови збудження переходу:

• у вхідному вузлі має знаходитись зелений маркер (значення виразу дуги, спрямованої від вузла стану світлофора до переходу від зеленого до жовтого світла, графічно зображується зеленим маркером);

• у разі спрацьовування переходу жовтий маркер може переміститись у вузол стану світлофора (значення виразу дуги, спрямованої від вузла стану світлофора до переходу від зеленого до жовтого світла, графічно зображується жовтим маркером).

Відображення станів моделі за допомогою маркерів різного кольору — один з можливих підходів до формальної побудови моделі, що відрізняється від моделі скінченного автомата, в якому кожний допустимий стан моделі зображується окремим вузлом.

Під час розроблення імітаційної моделі, яка повинна якомога точніше відображати дійсність, перед проектувальником стоїть надзвичайно складне завдання — пошук допустимих станів, дій та взаємозалежностей, які існують у модельованій системі, та опис їх за допомогою елементів мережі Петрі. Таким чином, розширюючи можливості базових елементів мережі Петрі (вузлів, дуг і переходів), можна створити модель практично будь-якої дискретно-подійної системи. Такі можливості надають програмні засоби для моделювання систем за допомогою розширених мереж Петрі.