Висновки

• Теорія масового обслуговування визначає залежність між параметрами потоків вимог, кількістю пристроїв обслуговування і їх продуктивністю, а також між режимами функціонування СМО та її ефективністю.

• Основні теоретичні результати теорії масового обслуговування отримано для систем, в яких процеси надходження та обслуговування вимог є марківськими та напівмарківськіми.

• Замкнена мережа СМО — це ізольована від зовнішнього середовища мережа, для якої не існує зовнішніх джерел і стоків вимог.

• Розімкнена мережа СМО — це мережа, в якій вимоги, що обробляються пристроями обслуговування, можуть надходити із зовнішнього середовища або спрямовуватись до нього.

• Операційний аналіз є методом дослідження мереж СМО, в основі якого лежать операційні змінні. Основні результати операційного аналізу формуються у вигляді співвідношень між операційними змінними.

• Умови функціонування мережі СМО визначає гіпотеза про баланс потоків у мережі: кількість вимог, що надійшли до деякого вузла протягом тривалого періоду часу, дорівнює кількості вимог, які залишили цей вузол.

Контрольні запитання та завдання

1. Розгляньте потік Ерланга r-го порядку. Як розподіляються проміжки часу між сусідніми вимогами? Поясніть, чому. До якого розподілу буде наближатись розподіл Ерланга у разі збільшення параметра r? Який розподіл матиме час надходження вимог, якщо r прямує до нескінченності?

2. Розгляньте К незалежних джерел вимог, для кожного з яких проміжки часу між сусідніми вимогами розподілені за експоненціальним законом з параметром _k, тобто кожне джерело є пуассонівським. Розгляньте сумарний потік від усіх джерел і доведіть, що цей потік теж є пуассонівським з параметром .

3. Розгляньте об'єднаний потік вимог із попереднього завдання і припустіть, що тепер його потрібно розбити на кілька потоків. Нехай р — це ймовірність того, що деяка вимога з об'єднаного потоку буде віднесена до підпотоку з номером k. Якщо інтенсивність сумарного потоку дорівнює вимог за одиницю часу і ймовірності р вибираються довільно, то кожний з підпотоків створює пуассонівський процес з інтенсивністю . Покажіть це.

4. Поясніть, чому система типу D/D/1 за умови  = 1 працює в сталому режимі й не має черги, а система типу М/М/1 за умови  = 1 переходить у нестаціонарний режим, і черга росте до нескінченності. Що буде за умови накладення обмежень на довжину черги для системи типу М/М/1? У цьому випадку при будь-якому співвідношенні значень для інтенсивності надходження вимог  і швидкості обслуговування  ця система працюватиме в сталому режимі. Покажіть це.

5. З огляду на життєві ситуації наведіть кілька прикладів, які ілюструють роботу СМО. Розгляньте такі варіанти:

а) вимоги надходять до системи обслуговування по одній;

б) вимоги надходять до системи обслуговування пакетами;

в) порядок надходження відомий заздалегідь;

г) надходження повністю випадкове;

д) джерело вимог невичерпане або обмежене;

е) існує тільки одна черга або кілька черг;

ж) час перебування в черзі обмежений;

з) обслуговування виконується у дві фази.

Назвіть для наведених вами прикладів три-п'ять важливих характеристик, які потрібно було б розрахувати або виміряти для цих систем. За яких умов можна вважати вхідний потік вимог пуассонівським?

6. Опишіть, яким чином потрібно змінити роботу алгоритмів моделювання, описаних у розділі 2.6.4, щоб урахувати:

а) обмеження, накладені на довжину черги;

б) обмеження, накладені на час перебування в черзі;

в) наявність m однакових пристроїв для обслуговування вимог.

Під час реалізації алгоритму для третього варіанта розгляньте визначення одного із вільних пристроїв у порядку наданих їм номерів 1, 2, ..., m і у випадковому порядку. Поясніть, чому для першого способу визначення вільних приладів їх завантаження буде різним.

7. Продовжіть моделювання процесів обслуговування в магазині методом, описаним у розділі 2.6.2, до 20 вимог, задавши довільне значення часу надходження та часу обслуговування вимог. Побудуйте за допомогою програми Excel або пакета STATISTICA гістограму часу перебування вимог у черзі.

8. У якому випадку потік вимог з мережі (див. рис. 2.14) буде пуассонівським? Поясніть чому.

9. Які складності виникають під час розрахунків мереж СМО?

10. Для розрахунків яких систем можна застосовувати операційний аналіз?

11. Сформулюйте гіпотезу про баланс потоків у мережі СМО. Поясніть, як її можна використовувати під час розрахунків різних СМО.

12. На рис. 2.26 зображено графік спостереження за роботою СМО з одним пристроєм для обслуговування протягом 20 с її роботи. Проведені вимірювання показали, що A_i = 7 вимогам; В_i = 16 с; С_i = 10 вимог. Як видно на графіку, n_i(0) = 3 вимог і n_i(20) = n_i(0) + A_i + С_i = 0. Потрібно знайти вихідні операційні змінні: коефіцієнт завантаження U_i, продуктивність X_i, сумарний час чекання W_i та обслуговування S_i вимог, середню довжину черги N i середній час перебування вимоги в СМО.

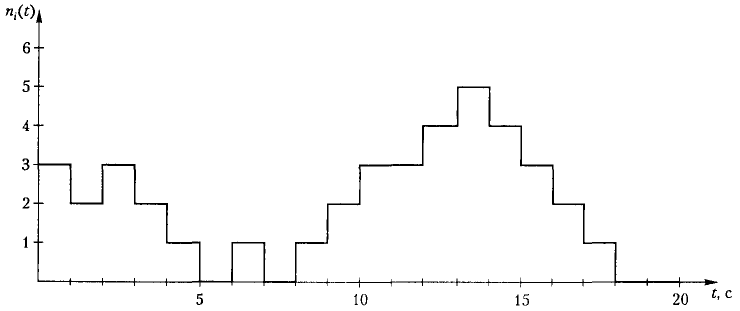
Рис. 2.26. Графік спостереження за роботою СМО

13. Деяка виробнича дільниця має L верстатів, які працюють 24 год на добу Н діб. Будь-який з верстатів може вийти з ладу в будь-який час. Якщо верстат зламався, його замінюють іншим, резервним, а зламаний направляють для ремонту в майстерню. Відремонтований верстат повертають до роботи.

У майстерні є три спеціалізовані дільниці для ремонту верстатів. Технологічний цикл ремонту починається на дільниці діагностики, де визначаються причина виходу з ладу верстатів та необхідний вид ремонту. Діагностика триває A₁  В₁ год (розподіл – рівномірний). Ремонт виконується в механічних і електричних майстернях. За статистичними даними, отриманими за результатами аналізу виходу з ладу верстатів, 75% випадків становить відмова електричного обладнання верстатів, а 25% – механічного. Діагностикою зайнято m₁ робітників, ремонтом механічного обладнання — m₂, а ремонтом електричного обладнання — m₃ робітників.

Досвід експлуатації свідчить, що на діагностику витрачається A₁  В₁ год, на ремонт електричного обладнання верстата — A₂  В₂ год, а на ремонт механічного обладнання – A₃  В₃ год (розподіл — рівномірний). Якщо верстат використовується у виробництві, час напрацювання на відмову має експоненціальний розподіл з параметром Т год. Час для перевезення верстатів із цеха в майстерню та в зворотному напрямку незначний, і його не враховують. Між робітниками в майстерні немає ніяких відмінностей, як і між верстатами.

Керівнику необхідно визначити, скільки робітників треба найняти для роботи в майстерні на кожній дільниці, щоб мінімізувати час ремонту обладнання. Час спостереження за системою — Н діб. Необхідні дані наведено в табл. 2.2.

Таблиця 2.2. Параметри моделювання роботи майстерні

L	Т	A1  В1	A2  В2	A3  В3	H
50	160	2  1	30  10	45  5	360

14. У касовому залі з продажу квитків на літаки працює 20 касирів, кожний за своїм терміналом. Термінали підключено до двохпроцесорного кластерного сервера, який обробляє запити клієнтів на будь-якому з двох процесорів. Середній час обробки запиту процесором становить 10 с. Кожний касир працює із системою в режимі «запит-відповідь», тобто не посилає новий запит, доки не отримає відповідь на попередній. Середній час введення запиту касиром становить 30 с. До касирів постійно є черга клієнтів. Знайдіть середній час відповіді системи на запит клієнтів. Побудуйте залежність цього часу від кількості працюючих касирів, яка може змінюватись від 1 до 20 чоловік.

Система массового обслуживания (СМО) — система, которая производит обслуживание поступающих в неё требований. Обслуживание требований в СМО производится обслуживающими приборами. Классическая СМО содержит от одного до бесконечного числа приборов. В зависимости от наличия возможности ожидания поступающими требованиями начала обслуживания СМО подразделяются на

1. системы с потерями, в которых требования, не нашедшие в момент поступления ни одного свободного прибора, теряются;

2. системы с ожиданием, в которых имеется накопитель бесконечной ёмкости для буферизации поступивших требований, при этом ожидающие требования образуют очередь;

3. системы с накопителем конечной ёмкости (ожиданием и ограничениями), в которых длина очереди не может превышать ёмкости накопителя; при этом требование, поступающее в переполненную СМО (отсутствуют свободные места для ожидания), теряется.

Выбор требования из очереди на обслуживание производится с помощью так называемой дисциплины обслуживания. Их примерами являются FCFS/FIFO (пришедший первым обслуживается первым), LCFS/LIFO (пришедший последним обслуживается первым), random  (англ.)(случайный выбор). В системах с ожиданием накопитель в общем случае может иметь сложную структуру.

Основные понятия СМО

Требование (заявка) — запрос на обслуживание.

Входящий поток требований — совокупность требований, поступающих в СМО.

Время обслуживания — период времени, в течение которого обслуживается требование.

Математическая модель СМО — это совокупность математических выражений, описывающих входящий поток требований, процесс обслуживания и их взаимосвязь.

Теория массового обслуживания (теория очередей) — раздел теории вероятностей, целью исследований которого является рациональный выбор структуры системы обслуживания и процесса обслуживания на основе изучения потоков требований на обслуживание, поступающих в систему и выходящие из неё, длительности ожидания и длины очередей. В теории массового обслуживания используются методы теории вероятностей и математической статистики.

Теорию потока однородных событий, которая легла в основу теории массового обслуживания, разработал советский математик А. Я. Хинчин.

Первые задачи ТМО (Теории Массового Обслуживания) были рассмотрены сотрудником Копенгагенской телефонной компании, ученым Агнером Эрлангом, в период между 1908 и 1922 годами. Стояла задача упорядочить работу телефонной станции и заранее рассчитать качество обслуживания потребителей в зависимости от числа используемых устройств.

Имеется телефонный узел (обслуживающий прибор), на котором телефонистки время от времени соединяют отдельные номера телефонов друг с другом. Системы массового обслуживания (СМО) могут быть двух видов: с ожиданием и без ожидания (то есть с потерями). В первом случае вызов (требование, заявка), пришедший на станцию в момент, когда занята нужная линия, остается ждать момента соединения. Во втором случае он «покидает систему» и не требует забот СМО.

Однородный поток

Поток заявок однороден, если:

• все заявки равноправны,

• рассматриваются только моменты времени поступления заявок, т.е. факты заявок без уточнения деталей каждой конкретной заявки.

Поток без последействия

Поток без последействия, если число событий любого интервала времени ( , ) не зависит от числа событий на любом другом непересекающемся с нашим ( , ) интервале времени.

Стационарный поток

Поток заявок стационарен, если вероятность появления n событий на интервале времени ( , ) не зависит от времени , а зависит только от длины этого участка.

Простейший поток

Однородный стационарный поток без последействий является простейшим, потоком Пуассона.

Число событий такого потока, выпадающих на интервал , распределено по Закону Пуассона:

Пуассоновский поток заявок удобен при решении задач ТМО. Строго говоря простейшие потоки редки на практике, однако многие моделируемые потоки допустимо рассматривать как простейшие.

Мгновенная плотность (интенсивность) потока равна пределу отношения среднего числа событий, приходящихся на элементарный интервал времени ( , ) к длине интервала ( ), когда последний стремится к нулю.

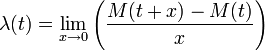
или, для простейшего потока,

где равно математическому ожиданию числа событий на интервале .