Принципи прийняття рішень

Розглянемо деякі найпоширеніші принципи прийняття рішень для багатокритерійних задач в умовах визначеності (детермінованості).

Згідно з принципом Джофріона розв’язок задачі визначається співвідношенням

де компоненти вектора – розв’язки n однокритерійних задач оптимізації за кожною складовою векторного критерію.

Відповідно до принципу Джофріона оптимальним уважають розв’язок, для якого максимально досягається мета в сенсі оптимізації кожного окремо взятого критерію. Однак для більшості задач це призводить до порушення умови раціональності, тобто найчастіше не існує допустимих розв’язків, для яких максимум досягається водночас за всіма критеріями.

Так, на рис. 4.12, а не існує допустимого розв’язку, який був би оптимальним у сенсі принципу Джофріона, а на рис. 4.12, b – існує.

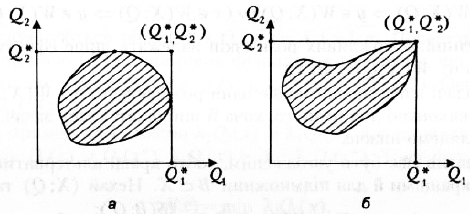
Рис. 4.12. Оптимальні розв'язки за принципом Джофріона

Принщп повного розв’язку, запроваджений В.Дінкельбахом, визначає розв’язок задачі як

W_v(X, Q) = Р(Х),

тобто розв’язком задачі вважається множина Парето-оптимальних рішень. Однак, оскільки постановку багатокритерійної задачі прийняття рішень орієнтовано на повне чи часткове розв’язання конфлікту, повний розв’язок теж уважають нераціональним. Отже, принципи Джофріона та повного розв’язку – це певні граничні випадки, зумовлені лише виглядом задачі прийняття рішення. Тому інші можливі принципи впорядковані в цих межах, тобто для довільного принципу прийняття рішень справедливі співвідношення

а в разі існування рішення, оптимального за Джофріоном,

Принцип корисності визначає оптимальний розв’язок, виходячи з припущення про існування відношення повного порядку на множині альтернатив, що залежить від складових критеріїв векторного критерію оптимальності (він раціональний, коли це відношення монотонне та неперервне на Rⁿ).

Цей принцип веде до співвідношення

тобто оптимальним є той розв’язок, для якого значення функції корисності максимальне.

Принцип ідеального розв’язку ґрунтується на припущенні про існування «ідеального» (можливо, недопустимого) розв’язку та метрики, за допомогою якої можна виміряти «віддаль» від довільного допустимого розв’язку до ідеального. Уважають, що координати ідеального розв’язку та метрики може визначити децидент. Множина оптимальних розв’язків згідно з цим принципом є наступною

де – віддаль в просторі критеріїв між ідеалом Q^* та довільною альтернативою х, виміряна за допомогою метрики . Оптимальними вважають розв'язки, найближчі до ідеального.

Принцип аналізу окремих складових векторного критерію базується на припущенні про те, що децидент може надати додаткову інформацію, потрібну для такого аналізу. Цей принцип реалізовано в методах переведення критеріїв у обмеження, методі послідовних поступок та інших.

4.2. Методи розв’язання багатокритерійних задач

Методи глобального критерію

Для усунення невизначеності мети застосовують два основні підходи.

1. Вважають, що мету достатньо адекватно відображає множина критеріїв, і тому постає багатокритерійна задача.

2. Вважають, що задано множину альтернатив, які можна вибирати з цієї множини за допомогою покрокового діалогу з децидентом, будуючи послідовність слабших бінарних відношень для звуження первісної множини альтернатив.

Представниками першого підходу є різноманітні методи згортання критеріїв, а також методи поступок, а другого – методи ELECTRE.

Лінійні та мультиплікативні згортання

Найчастіше множину критеріїв зводять до одного глобального та розв’язують класичну однокритерійну задачу. Однак застосування цього підходу має суттєві вади, одна з яких полягає в тому, що неможливо отримати деякі з оптимальних за Парето розв’язків (як видно з рис. 4.11, лінійне згортання не дає змоги одержати певні оптимальні за Парето розв’язки за будь-яких значеннях вагових коефіцієнтів) [42].

Методи згортання критеріїв зводять первісну задачу до однокритерійної задачі такого вигляду:

Найуживанішими методами згортання є лінійне згортання ненормованих та нормованих критеріїв.

За допомогою лінійного згортання глобальний критерій подається у вигляді лінійної комбінації компонентів векторного критерію якості з ваговими коефіцієнтами, основне призначення яких – врахування відносної важливості критеріїв:

де – і-та компонента векторного критерію якості, – ваговий коефіцієнт, що відображає відносну важливість і-го критерію.

Лінійне згортання нормованих критеріїв ґрунтується на ідеї зведення часткових критеріїв до безрозмірних величин з інтервалом можливих значень кожного з них [0, 1]. Щоб виконати таке перетворення, децидент має зазначити для кожного з критеріїв межі його зміни від мінімального значення до максимального та коефіцієнти відносної важливості нормованих критеріїв :

Головною проблемою цих методів є виявлення точних значень вагових коефіцієнтів. Найчастіше ця процедура суб’єктивна. Окрім того, коефіцієнти в методі лінійного згортання мають бути розмірними величинами, тому що критерії можуть мати різну розмірність. Щоб позбутися цієї вади в згортанні нормованих критеріїв, окремі критерії спочатку нормують (нормовані критерії безрозмірні та змінюються в інтервалі від 0 до 1).

Проте нормовані критерії, що з’являються унаслідок такого «вдосконалення», не мають змістовної інтерпретації, і тому об’єктивне визначення вагових коефіцієнтів іще більше ускладнюється. Отже, невизначеність мети, спричинена багатокритерійністю, не зменшується, а переходить в іншу форму – виникає проблема обчислення значень вагових коефіцієнтів [29].

З іншого боку, у разі опуклої області значень векторного критерію лінійне згортання можна використати для отримання кількох розв'язків, оптимальних за Парето (теорема 4.1), змінивши значення вагових коефіцієнтів. Це дає децидентові можливість у діалозі дослідити саме ту частину області Парето, яка найбільше його цікавить.

Адитивні згортання мають іще одну ваду – значення одного зі складових критеріїв може бути дуже великим унаслідок того, що значення інших мінімальні. Така ситуація є вкрай небажаною. Наприклад, конструюючи літак зі складовими критеріями економічності та швидкості польоту, за певних значень вагових коефіцієнтів можна отримати максимальне значення економічності за рахунок того, що швидкість польоту становитиме 0, а такий літак не потрібен нікому.

Щоб уникнути таких ситуацій, було запропоновано варіанти мультипликативного згортання у звичайному (4.2) та нормованому (4.3) вигляді:

	(4.2)
	(4.3)

Для таких згортань різке зменшення значення хоча б одного часткового критерію різко зменшує значення глобального. Критерії такого виду широко використовуються в економічних дослідженнях (досить лише згадати виробничі функції). Однак головна проблема – обчислення значень вагових коефіцієнтів – залишається нерозв’язаною.