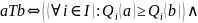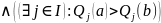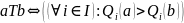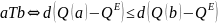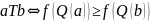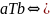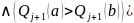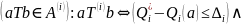Принципи вибору та бінарні відношення

Для розв’язання багатокритерійних задач сформульовано низку принципів вибору, що утворюють певну структуру S механізму вибору, яку найчастіше можна подати як певне бінарне відношення Р.

У моделі багатокритерійного оцінювання властивості кожної альтернативи відображаються в просторі критеріїв, і вибір виконують, порівнюючи образи альтернатив у цьому просторі. Структуру механізму вибору, породжену застосуванням того чи іншого принципу вибору, описують за допомогою певних класів бінарних відношень – координатних, модульних, координатно-модульних [5].

Таблиця 4.7. Бінарні відношення, використовувані в принципах вибору

Принцип вибору	Бінарне відношення
Парето
Слейтера
Джофріона
За еталоном
Згортка критеріїв
Лексикографічний
Послідовних поступок

Означення 4.1. Бінарне відношення, що залежить лише від знаків різниць складових значень векторів критеріїв Q(a) = (Q₁(a), …, Q_n(a)) та Q(b) = (Q₁(b), …, Q_n(b)) для пари альтернатив а та b, називається координатним, тобто

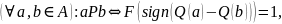
де А – носій відношення Р, 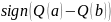– вектор знаків різниць відповідних компонент векторів критеріїв,

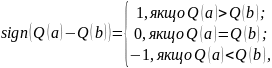
F – логічна функція, що має значення 1, коли аРb, та 0, коли .

Означення 4.2. Бінарне відношення, що залежить лише від значень модулів різниць векторів Q(a) та Q(b) альтернатив а та b, називається модульним, тобто

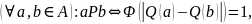
де 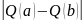– вектор модулів різниць відповідних компонент критеріїв, Ф – логічна функція, що має значення 1, коли аРb, та 0, коли .

Означення 4.3. Бінарне відношення, що залежить від знаків і модулів різниць однойменних складових вектора критеріїв, називається координатно-модульним, тобто

Бінарні відношення, що використовуються в деяких принципах вибору, і є складовими структур механізмів вибору, наведено в таб. 4.7. Це складові структур механізмів вибору. Згідно з принципом Парето, альтернатива а краща, ніж альтернатива b, якщо значення всіх критеріїв для неї не менші, ніж значення критеріїв для b та хоча б за одним критерієм альтернатива а краща, ніж b.

Приклад 4.10. Потрібно побудувати й застосувати механізм вибору 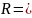, до бінарного відношення Т, породженого за принципом Парето, для обрання кращих альтернатив із множини A = {х₁, x₂, х₃, x₄}. Для кожної альтернативи задано образи в просторі трьох критеріїв: Q(х₁) = (1, 4, 8)^T, Q(x₂) = (3, 4, 7)^T, Q(х₃) = (2, 5, 9)^T, Q(x₄) = (3, 2, 6)^T.

За допомогою безпосереднього порівняння побудуємо бінарне відношення Т(x₂Тx₄, x₃Тx₁):

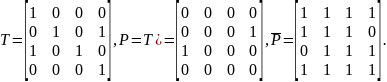
Мажоранти цього відношення – , (в останній матриці другий і третій стовпці складаються з 1) тобто результат вибору являє собою множину з двох оптимальних за Парето альтернатив .

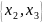Приклад 4.11. Потрібно побудувати та застосувати механізм вибору до бінарного відношення Т, породженого за принципом Слейтера, для вибору кращих альтернатив із множини A = {х₁, x₂, х₃, х₄, x₅, х₆, x₇}. Для кожної з них задано образи в просторі двох критеріїв: Q⁽¹⁾ = (8, 2), Q⁽²⁾= (6, 2), Q⁽³⁾ = (7, 1), Q⁽⁴⁾ = (5, 5), Q⁽⁵⁾ = (1, 8), Q⁽⁶⁾ = (1, 7), Q⁽⁷⁾ = (4, 3). Треба визначити множину альтернатив, оптимальних за Парето й за Слейтером.

За допомогою безпосереднього порівняння побудуємо бінарне відношення Т.

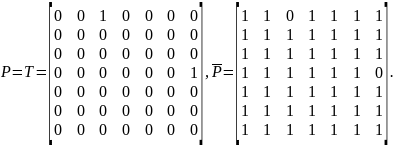
Отже, множина оптимальних за Слейтером альтернатив – {х₁, x₂, х₄, x₅, х₆}.

Приклад 4.12. Задано образи множини альтернатив A = {х₁, x₂, х₃, х₄, x₅} у просторі критеріїв: Q(х₁) = (5, 6)^T, Q(x₂) = (6, 9)^T, Q(х₃) = (5, 4)^T, Q(х₄) = (4, 3)^T, Q(x₅) = (6, 9)^T.

Потрібно зробити вибір згідно з механізмом , де Т – бінарне відношення, побудоване за принципом Джофріона. Його матриця має вигляд

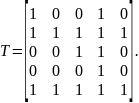
Максимуми цього відношення – 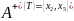, тобто дві найкращі альтернативи .

Принцип вибору за еталоном реалізують шляхом визначення еталона – певної точки в просторі критеріїв, досягнення якої найбажаніше для децидента, а також метрики для вимірювання віддалі від альтернатив до еталона. Принцип еталона являє собою узагальнення принципу ідеального розв’язку, тому що еталоном може бути довільна точка в просторі критеріїв. Обирають альтернативи, найближчі до еталона, тобто максимуми відповідного відношення.

Приклад 4.13. Задано образи множини альтернатив A = {х₁, x₂, х₃, х₄} в просторі критеріїв: Q(х₁) = (2, 2)^T, Q(x₂) = (4, 1)^T, Q(х₃) = (6, 2)^T, Q(х₄) = (0, 5)^T, – а також еталон Q^E = (4, 6)^T та метрику 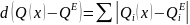. Потрібно знайти найкращі альтернативи для механізму вибору , де Т – бінарне відношення, породжене принципом вибору за еталоном.

Побудуємо відношення Т, обчисливши віддалі від кожної альтернативи до еталона:

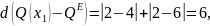
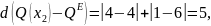
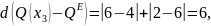
Отже, обрано множину альтернатив 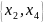, найближчих до еталона.

Механізм вибору за згорткою критеріїв можна подати у вигляді , де Т – бінарне рефлексивне відношення, породжене згорткою.

Для реалізації лексикографічного принципу вибору потрібні інші припущення, ніж для згортки. Необхідністю є впорядкування критеріїв за важливістю з послідовним порівнянням відповідних компонент. Якщо альтернатива а краща, ніж b, за найважливішим критерієм, то вона взагалі краща, ніж b.

Приклад 4.14. Потрібно вибрати найкращу альтернативу з таких: Q(х₁) = (2, 6, 10, 5, 14)^T, Q(x₂) = (10, 5, 8, 12, 6)^T, Q(х₃) = (10, 5, 8, 6, 10)^T, Q(х₄) = (2, 8, 3, 4, 12)^T. Застосуємо механізм вибору , де Т – бінарне антирефлексивне відношення, побудоване за лексикографічним принципом, і критерії впорядковано так: .

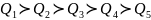Побудуємо бінарне відношення Т, виходячи із заданого впорядкування критеріїв:

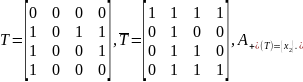
Застосувавши принцип лексикографічного впорядкування, оберемо альтернативу х₂.

У методі переведення критеріїв в обмеження реалізовано принцип вибору за головним критерієм. Суть цього принципу полягає у виборі головного критерію, для порівняння альтернатив і фіксуванні вектора Q^M допустимих рівнів інших критеріїв. Звичайно, у разі довільного задання складових вектора Q^M завжди існує небезпека порожнього вибору внаслідок завищених вимог до значень критеріїв, які окремо реалізовні, а в сукупності – ні.

Приклад 4.15. Потрібно вибрати найкращі альтернативи з множини A = {х₁, x₂, х₃, х₄, x₅} за принципом головного критерію та побудувати відповідний механізм вибору на основі породженого ним бінарного відношення Т, якщо задано образи альтернатив у просторі критеріїв Q(х₁) = (10, 8, 12)^T, Q(x₂) = (10, 4, 8)^T, Q(х₃) = (10, 9, 7)^T, Q(х₄) = (8, 10, 12)^T, Q(х₅) = (6, 3, 15)^T та допустимі значення 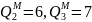, і головний критерій – Q₁.

Альтернативам, для яких значення складових критеріїв Q₂ та Q₃ менші за допустимі значення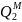 і 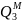, відповідають стовбець і рядок із нулів, а в графовому поданні – ізольовані вершини, які не слід обирати. Потрібний результат отримаємо, обравши максимуми на відповідній підмножині А, якій не належать ізольовані вершини. Отже, механізм вибору має вигляд , де 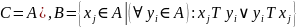, Т_C – звуження відношення Т на множину С, С⁺ – множина максимумів звуженого відношення Т_C. Згідно з формулюванням принципу головного критерію, матриця бінарного відношення Т має вигляд

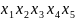
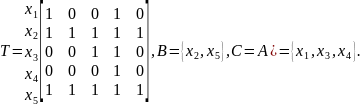
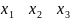
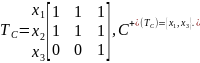
Отже, оберемо альтернативи х₁ та х₃.

Принцип послідовних поступок не має вад, властивих принципам згортки критеріїв, лексикографічному, вибору за еталоном, головного критерію, здебільшого завдяки більшій гнучкості.

Приклад 4.16. Задано множину альтернатив A = {х₁, x₂, х₃, х₄, x₅, х₆} і множину образів альтернатив у просторі критеріїв Q(х₁) = (10, 8, 12, 6, 13)^T, Q(x₂) = (12, 6, 8, 4, 5^T, Q(х₃) = (14, 4, 7, 3, 2)^T, Q(х₄) = (10, 7, 4, 5, 18)^T, Q(x₅) = (13, 5, 10, 3, 4)^T, Q(х₆) = (16, 3, 5, 2, 1)^T. Потрібно вибрати найкращі альтернативи, вважаючи, що критерії впорядковано за важливістю в послідовності .

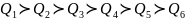Механізм вибору полягатиме у звуженні множини альтернатив, що розглядаються на кожному кроці, з використанням поступки. На поточному i-му кроці треба виконати такі дії.

1. Знайти максимальне значення критерію Q_i на поточній множині-носієві А: .

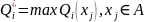2. Вирішити, чи доцільно задавати поступку _i за i-им критерієм (тобто чи згоден децидент погіршити значення на _i одиниць). Якщо немає сенсу зменшувати значення , тобто _i = 0, то буде вибрано альтернативи, для яких на цьому кроці досягнуто значення , і процес припиняється.

3. Побудувати відношення Т, застосувавши принцип послідовних поступок за правилом

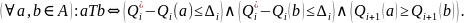
4. Звузити множину-носій А, виключивши з неї альтернативи, які не перебувають у відношенні Т з жодними іншими (вони відповідають ізольованим вершинам у графовому поданні):

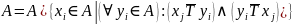
Якщо саrd(A) = 1, то процес припиняється, і буде вибрано єдину альтернативу, що залишилася. Така ситуація виникає тоді, коли задана поступка така мала, що до альтернатив, які розглядаються, неможливо додати жодну іншу з поточної множини А, окрім тієї, якій відповідає значення . Якщо переглянуто всі складові критеріїв (і = n), то вибирають усі альтернативи, що належать поточній множині А. На першому кроці

A = {х₁, x₂, х₃, х₄, x₅, х₆}, 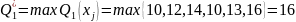, х_j  А.

Проаналізувавши значення , децидент дійде висновку, що допустиме максимальне падіння якості за критерієм Q₁ на 4 одиниці, тобто ₁ = 4. Застосувавши правило кроку 3, отримаємо відповідне відношення та звузимо згідно з правилом 4 поточну множину-носій А:

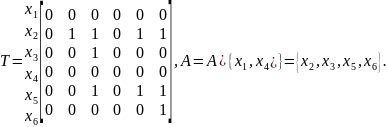
Отже, на другому кроці можна вибирати з чотирьох альтернативи 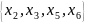. Визначимо .

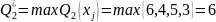Задамо поступку ₂ = 1. Відношення Т для другого кроку та поточна множина такі:

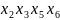
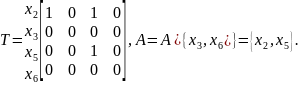
На третьому кроці визначимо 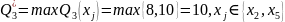. Задамо поступку ₃ = 1.

Побудуємо відношення Т для третього кроку та звузимо множину А:

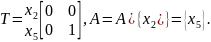
Оскільки залишилась одна альтернатива (card(A) = 1), то припинимо процес, і вважатимемо результатом вибору альтернативу х₅.

Одні й ті самі механізми вибору можна формально подавати кількома способами. Скажімо, вибір за принципом Парето можна розглядати як агрегацію відношень, кожне з яких породжене відповідною складовою вектора критеріїв. Окрім того, завжди можна замість мажорант шукати максимуми двоїстого відношення, тому що справедливе співвідношення А₊(Р) = A₊(P^d).

У разі пошуку максимумів відношення зазвичай уважають рефлексивним, тобто наявне відношення Q доповнюють до рефлексивного Р = Q  Е, де Е – діагональне відношення. Для визначення мажоранти відношення вважають антирефлексивним, тобто Р = Q\E. Якщо потрібно вибирати недоміновані альтернативи у квазіпорядку, то доцільно факторизувати його за симетричною складовою (отримане фактор-відношення буде відношенням порядку), звести до антирефлексивного вигляду та обрати мажоранти зведеного відношення. Отже, кожна мажоранта може включати в себе одну чи декілька еквівалентних за якістю альтернатив первісного відношення, з яких і треба робити остаточний вибір.