34. Теоремы о пределах последовательности.
Теорема 1: (необходимый признак числовой последовательности):
если последовательность сходится, то она ограничена. , если последовательность неограниченна, то она расходится.
Теорема Вейерштрасса: сформируем достаточный признак числовой последовательности: всякая ограниченная монотонная последовательность имеет предел.
Теорема
: если две последовательности {xn}и
{yn}
сходятся, т.е. имеют конечные пределы,
то сходятся также сумма, разность,
произведение, частное этих
последовательностей, т.е.:
=>
и
тд.
Теорема:
если
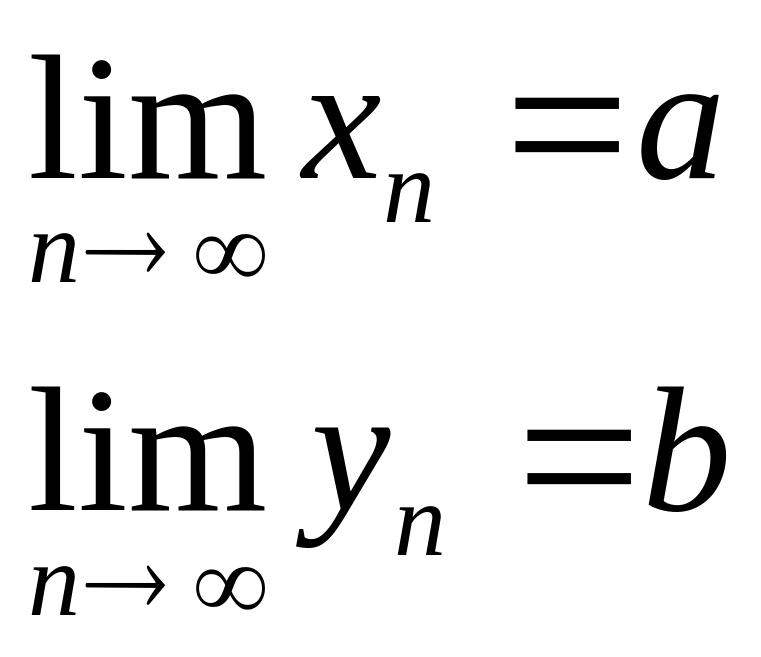и
начиная с некоторого номера выполняется
неравенство xn
yn,
то а
b.
Доказательство:
допустим,
что а>b.
Из равенств
следует,
что для любого
>0
найдется такое натуральное число N(
),
что при всех n>N(
)
будут выполняться неравенства
и
т.е.
и
.
Возьмем
.
Тогда:
отсюда
следует, что xn>yn,
это противоречит условию xn
yn
следовательно, а
b.
35. Предел функции.
Сформулируем два, эквивалентных между собой, определения предела функции в точке:
Определение
( по Коши):
число А называется пределом функции в
точке х0
, если для любого положительного
найдется
такое положительное число
,
что для всех х
х0
, удовлетворяющих неравенству
,
выполняется неравенство
.
Коротко это определение:
.
Определение (по Гейне):
Число
А называется пределом функции
в точке х0, если для любой последовательности
допустимых значений аргумента хn,
сходящейся к х0, последовательность
соответствующих значений функции
,
,
сходится к числу А.
Односторонние
пределы:
число
А называется пределом функции
слева в точке x0,
если для любого число
>0
существует число
=
(
)>0
такое, что при
выполняется
неравенство
.
Предел
слева записывают так:
Аналогично определяется предел функции справа:
.
Пределы функции слева и справа называются односторонними пределами.
Предел
функции при
:
Число
А называется пределом
функции при
,
если для любого положительного числа
существует такое число М=М(
)
>0, что при всех х, удовлетворяющих
неравенству
выполняется
неравенство
.
Коротко:
36. Бесконечно малые и бесконечно большие функции.
Функция
называется бесконечно
большой при
,
если для
любого числа M>0
существует число
=
(М)>0,
что для всех х, удовлетворяющих
неравенству 0<
,
выполняется неравенство
.
Записывают
.
Коротко:
Функция
называется бесконечно
большой при
,
если для
любого числа M>0
найдется такое число N=N
(М)>0, что для всех х, удовлетворяющих
неравенству
,
выполняется неравенство
.
Коротко:
Всякая бесконечно большая функция в окрестности точки х0 является неограниченной в этой окрестности.
Бесконечно
малая функция:
Функция
называется бесконечно малой при
,
если
:
для любого числа
>0
найдется число
>0
такое, что для всех х, удовлетворяющих
неравенству 0<
,
выполняется неравенство
.
Теорема: алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
Док-во:
Теорема: произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.
Док-во:
Следствие: так как всякая б.м.ф. ограничена, то из теоремы вытекает произведение двух б.м.ф. есть функция бесконечно малая.
Следствие: произведение б.м.ф. на число есть функция бесконечно малая.
Теорема: частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.
Док-во:
Теорема: если функция - бесконечно малая, то обратная ей функция – бесконечно большая и наоборот.
Док-во: