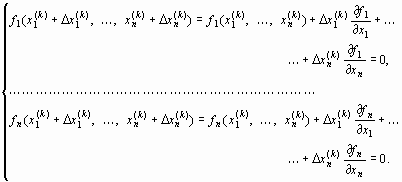- •1. Метод Гаусса
- •2. Обратная матрица
- •[Править]Свойства обратной матрицы
- •[Править]Способы нахождения обратной матрицы
- •[Править]Точные (прямые) методы [править]Метод Гаусса—Жордана
- •[Править]с помощью матрицы алгебраических дополнений
- •[Править]Использование lu/lup-разложения
- •[Править]Примеры [править]Матрица 2х2
- •3. Метод Крамера
- •[Править]Описание метода
- •[Править]Пример
- •[Править]Вычислительная сложность
- •Метод половинного деления
- •Метод секущих
- •Метод простых итераций
- •Метод Вегштейна
- •Метод Ньютона
- •5,6. Смотри 4.
- •8. Смотри 4.
- •9. Сходимость метода простых итераций
- •10. Метод Рыбакова
- •13. Аппроксимация функций методом наименьших квадратов
- •14. Вычисление производной с помощью конечных разностей
- •15.Интерполяционный многочлен Лагранжа
- •[Править]Определение
- •[Править]Применения
- •[Править]Случай равномерного распределения узлов интерполяции
- •16.Интерполяционные формулы Ньютона
- •19. Правило Рунге
- •[Править]Применение правила Рунге [править]Оценка точности вычисления определённого интеграла
- •20. Счет с автоматическим выбором шагов интегрирования
- •21.Задача Коши
- •22.Метод Эйлера
- •23.Метод Рунге — Кутты
- •[Править]История
- •[Править]Примеры
- •[Править]Однородные уравнения
- •[Править]Уравнение Бернулли
- •24.Метод наименьших квадратов
- •[Править]История
- •[Править]Примеры
- •25. Метод прогонки
- •[Править]Описание метода
- •26. Метод последовательных приближений
- •27. Разложение функций в степенной ряд. Ряд Тейлора.
- •28.Краевая задача
- •29. Метод конечных разностей, или метод сеток
- •Теорема
- •Теорема
10. Метод Рыбакова
Для дальнейшего нам понадобится теорема Лагранжа. Приведем(напомним) ее формулировку: Если функция f является непрерывной на замкнутом отрезке [a,b] и существует конечная производная на открытом отрезке(a,b),то обязательно найдется точка a<с<b такая, что будет выполняться равенство:
f(b)-f(a)=f (c)(b-a).
Геометрический смысл этой теоремы заключается в том, что найдется
касательная, параллельная прямой, проходящей через точки (a, f(a)) и (b, f(b)).
Теорема. Если для функции f(x) существует конечная производная на отрезке, то для метода Рыбакова всегда будет выполняться неравенство
xn < x, где f(x)=0. Другими словами xn не “перепрыгнет” через корень х и, таким образом, последовательно будут найдены все корни.
Доказательство. Предположим что число x является корнем уравнения
f(x)=0 и выполняется неравенство xn <x< xn+1, . По теореме Лагранжа существует такая точка с, что a xn<с<xb и выполняется равенство
|f(x)-f(xn)|= |f (c) (x- xn)|. Так как a<с<b, то значит и |f(c)|<M. Учтем, что f(x)=0 и xn<x, а значит |(x- xn)|= (x- xn).
Поэтому справедливо неравенство:
|f(xn)|= |f (c) | | (x- xn)|=|f(c) |(x- xn)<M(x- xn). Так как M>0, то отсюда |f(xn)|/M<(x- xn) и окончательно получим x> xn+|f(xn)|/M =xn+1 .Таким образом пришли к противоречию x> xn+1 с первоначальным предположением
xn <x< xn+1 .
11. Метод Рыбакова. Алгоритм осуществляет поиск корней на заданном промежутке [a,b]. Чтобы условия сходимости были обеспечены на всем интервале, F'(xi) заменена некоторой константой M, которая выбирается из условия M ≥ | F'(x)|, a<x<b. Не следует задавать M с большим запасом, так как в этом случае поиск пойдет слишком медленно. Чтобы процесс не увязал в точках, где F(x)=0, в алгоритм вводится интервал различимости корней e (в программе задано e =10-3). Положить x=a. Пока x≤b, повторять: пока F(x)╧0, повторять: x=x+|F(x)|/M; отпечатать x; положить x=x+e. 10 INPUT "a",A,"b",B,"M",C 20 D=...f{A}...:A=A+ABS D/C:IF A>B THEN 10 30 IF C+D=C;PRINT A:A=A+1E-3 40 GOTO 20 Размер: 70+, D Пример: F(x)=sin(x-0,3)+0,2x; a=-1; b=1; M=1,2. В программе: MODE 5 20 D=SIN (A-.3)+.2*A: ... Ответ: x*=0,249982623.
12. В отличие от систем линейных уравнений для систем нелинейных уравнений не известны прямые методы решения. Лишь в отдельных случаях систему можно решить непосредственно. Например, для системы из двух уравнений иногда удается выразить одно неизвестное через другое и таким образом свести задачу к решению одного нелинейного уравнения относительно одного неизвестного. Поэтому итерационные методы для нелинейных систем приобретают особую актуальность.
Метод Ньютона.
Рассмотрим нелинейную систему уравнений
|
(23) |
или в векторной форме
f (x) = 0, |
(23 ') |
где
f ![]() x
x ![]()
Для решения системы (23? ) будем пользоваться методом последовательных приближений.
Предположим, известно k-е приближение
x(k) = ![]()
одного
из изолированных корней x = ![]() векторного
уравнения (23 '). Тогда точный корень
уравнения (23') можно представить в виде
векторного
уравнения (23 '). Тогда точный корень
уравнения (23') можно представить в виде
х = x(k) + D x(k), |
(24) |
где D x(k) =![]() -
поправка (погрешность корня).
-
поправка (погрешность корня).
Подставляя выражение (24) в (23'), будем иметь
f (x(k) + D x(k)) = 0. |
(25) |
Предполагая, что функция f (x) непрерывно дифференцируема в некоторой выпуклой области, содержащей x и x(k), разложим левую часть уравнения (25) по степеням малого вектора D x(k) , ограничиваясь линейными членами,
f (x(k) + D x(k)) = f (x(k)) + f ? (x(k)) D x(k) = 0 |
(26) |
или, в развернутом виде,
|
(26') |
Из формул (26) и (26') вытекает, что под производной f '(x) следует понимать матрицу Якоби системы функций f1, f2, ..., fnотносительно переменных x1, x2, ..., xn, т. е.
f ' (x)
= W(x)
= ,
,
или в краткой записи
f ' (x)
= W(x)
= ![]() (i,
j =
1, 2, …, n).
(i,
j =
1, 2, …, n).
Поэтому формула (26) может быть записана в следующем виде:
f (x(k) ) + W (x(k) ) D x(k) = 0
Если det W ( х )
=![]() ,
то D x(k) =
- W -1(x(k)) f (x(k)).
,
то D x(k) =
- W -1(x(k)) f (x(k)).
Отсюда видно, что метод Ньютона решения системы (23) состоит в построении итерационной последовательности:
x(k + 1) = x(k) - W -1(x(k)) f (x(k)) (k = 0, 1, 2, …). |
(27) |
Если все поправки становятся достаточно малыми, счет прекращается. Иначе новые значения xi используются как приближенные значения корней, и процесс повторяется до тех пор, пока не будет найдено решение или не станет ясно, что получить его не удастся.
Пример 9. Методом Ньютона приближенно найти положительное решение системы уравнений

исходя из начального приближения x0 = y0 = z0 =0,5.
Полагая:
х(0) =![]() , f (х) =
, f (х) = ,
,
имеем:
f (х) =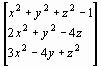
Отсюда
f ( х(0) ) =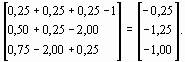
Составим матрицу Якоби
W(x)
= 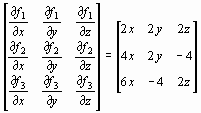
Имеем
W ( х(0) )
=  ,
причем D =
det W ( х(0) )
=
,
причем D =
det W ( х(0) )
= 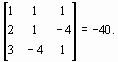
Следовательно, матрица W ( х(0) ) - неособенная. Составим обратную ей матрицу
W -1 ( х(0) )
= 
По формуле (27) получаем первое приближение
х(1) = x(0) -
W -1(x(0) ) f (x(0) )
=![]() -
- 
![]() =
=![]() +
+  =
= ![]() .
.
Аналогично находятся дальнейшие приближения. Результаты вычислений приведены в Таблице 3.
Таблица 3
Последовательные приближения корней
i |
x |
y |
z |
0 |
0,5 |
0,5 |
0,5 |
1 |
0,875 |
0,5 |
0,375 |
2 |
0,78981 |
0,49662 |
0,36993 |
3 |
0,78521 |
0,49662 |
0,36992 |
Останавливаясь на приближении x(3) , будем иметь:
x = 0,7852; y = 0,4966; z =0,3699.