[Править]История

Простейшие дифференциальные уравнения встречались уже в работах И. Ньютона и Г. Лейбница; термин «дифференциальные уравнения» принадлежит Лейбницу. Ньютон при создании исчисления «флюксий» и «флюент» ставил две задачи: по данному соотношению между флюентами определить соотношение между флюксиями; по данному уравнению, содержащему флюксии, найти соотношение между флюентами. С современной точки зрения, первая из этих задач (вычисление по функциям их производных) относится к дифференциальному исчислению, а вторая составляет содержание теории обыкновенных дифференциальных уравнений. Задачу нахождениянеопределённого интеграла F(x) функции f(x) Ньютон рассматривал просто как частный случай его второй задачи. Такой подход был для Ньютона как создателя основ математического естествознания вполне оправданным: в очень большом числе случаев законы природы, управляющие теми или иными процессами, выражаются в форме дифференциальных уравнений, а расчёт течения этих процессов сводится к решению дифференциального уравнения.^[1]

Основное открытие Ньютона, то, которое он счел нужным засекретить и опубликовал лишь в виде анаграммы, состоит в следующем: «Data aequatione quotcunque fluentes quantitae involvente fluxiones invenire et vice versa». В переводе на современный математический язык это означает: «Полезно решать дифференциальные уравнения». В настоящее время теория дифференциальных уравнений представляет собой трудно обозримый конгломерат большого количества разнообразных идей и методов, в высшей степени полезный для всевозможных приложений и постоянно стимулирующий теоретические исследования во всех отделах математики.^[2] [3]

[Править]Примеры

• Одно из простейших применений дифференциальных уравнений — решение нетривиальной задачи нахождения траектории тела по известным проекциям ускорения. Например, в соответствии со вторым законом Ньютона, ускорение тела пропорционально сумме действующих сил; соответствующее дифференциальное уравнение имеет вид  . Зная действующие силы (правая часть), можно решить это уравнение и, учитывая начальные условия (координаты и скорость в начальный момент времени), найти траекторию движения точки.

• Дифференциальное уравнение y' = y, вместе с начальным условием y(0) = 1, задаёт экспоненту: y(x) = e^x. Если x обозначает время, то эта функция описывает рост популяции в условиях неограниченности ресурсов и многое другое.

• Решением дифференциального уравнения y' = f(x), правая часть которого не зависит от неизвестной функции, являетсянеопределённый интеграл: 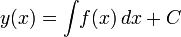 , где C — произвольная константа.

[править]Дифференциальные уравнения первого порядка

[править]Уравнения с разделяющимися переменными

Дифференциальное уравнение   называется уравнением с разделяющимися (отделяющимися) переменными, если его правая часть представима в виде y' = f₁(x)f₂(y). Тогда, в случае  , общим решением уравнения является  .

[править]Примеры физических задач, приводящих к уравнениям с разделяющимися переменными

[править]Охлаждение тела

Пусть T — температура тела, T₀ — температура окружающей среды (T > T₀). Пусть Q — количество теплоты, c — удельнаятеплоёмкость. Тогда количество теплоты передаваемое окружающей среде до выравнивания температур выражается формулой Q =mc(T − T₀), или, в дифференциальной форме,  . С другой стороны скорость отдачи тепла можно выразить в виде  , где k — некий коэффициент пропорциональности. Исключая из этих двух уравнений dQ получаем уравнение с разделяющимися переменными:

.

Общим решением этого уравнения является семейство функций  .