7. Линейные однородные (ло) ду n-го порядка
Уравнение вида b0 (x) y(n) + b1 (x) y(n – 1) + … + bn (x) y = g (x), где b0 (x) ≠ 0, b1 (x), … , bn (x), g (x) – заданные функции (от x), называются линейным ДУ n-го порядка.
Если свободный член g (x) 0, то это уравнение называется линейным однородным уравнением; если g (x) ≠ 0, то уравнение
b0 (x) y(n) + b1 (x) y(n – 1) + … + bn (x) y = g (x) называется неоднородным.
Линейные однородные дифференциальные уравнения n-го порядка имеют вид y(n) + a1 (x) · y(n – 1) + a2 (x) · y(n – 2) + … + an (x) · y = 0.
Если функции y1 = y1 (x), y2 = y2 (x), … , yn = yn (x) являются частными решениями этого уравнения, то его решением является функция y = c1y1 + c2y2 + … + cnyn .
8. Линейная зависимость и линейная независимость системы функций. Определитель Вронского
Функции y1, y2 , … , yn называются линейно независимыми на (a; b), если равенство α1y1 + α2y2 + … + αnyn = 0 выполняется лишь в случае, когда все числа αi = 0 (I = 1, 2, … , n); в противном случае (если хотя бы одно из чисел αi не равно нулю) функции y1, y2 , … , yn – линейно зависимы.
Функции y1 = y1 (x) и y2 = y2 (x) называются линейно независимыми на интервале (a; b), если равенство
α1y1 + α2y2 = 0, где α1 , α2 Э IR, выполняется тогда и только тогда, когда α1 = α2 = 0. Если хотя бы одно из чисел α1 или α2 отлично от нуля и выполняется равенство α1y1 + α2y2 = 0, то функции y1 и y2 называются линейно зависимыми на (a; b).
Определитель Вронского имеет вид:
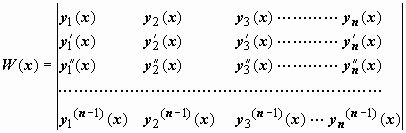
9. Теоремы о необходимых и достаточных условиях линейной зависимости и линейной независимости решений лоду
Т.: если дифференцируемые функции y1 (x) и y2 (x) линейно зависимы на (a; b), то определитель Вронского на этом интервале тождественно равен нулю.
Т.к. функции y1 и y2 линейно зависимы, то в равенстве α1y1 + α2y2 = 0 значение α1 или α2 отлично от нуля. Пусть α1 ≠ 0, тогда y1 =
– α2/α1 y2; поэтому для любого x Э (a; b)
| – α2/α1 y2 y2 |
W (x) = | – α2/α1 y’2 y’2 | = 0.
Т.: если функции y1 (x) и y2 (x) – линейно независимые решения уравнения y” + α1 (x) y’ + α2 (x) y = 0 на (a; b), то определитель Вронского на этом интервале нигде не обращается в нуль.
Из этих теорем следует, что вронскиан не равен нулю ни в одной точке интервала (a; b) тогда и только тогда, когда частные решения линейно независимы.
10. Фундаментальная система решений лоду. Структура общего решения лоду
Совокупность любых двух линейно независимых на интервале (a; b) частных решений y1 (x) и y2 (x) ЛОДУ определяет фундаментальную систему решений этого уравнения: любое произвольное решение может быть получено как комбинация y = α1y1 (x) + α2y2 (x).
Структура общего решения ЛОДУ: если два частных решения y1 = y1 (x) и y2 = y2 (x) ЛОДУ y” + α1 (x) y’ + α2 (x) y = 0 образуют на интервале (a; b) фундаментальную систему, то общим решением этого уравнения является функция y = c1y1 + c2y2, где c1 и c2 – произвольные постоянные.