(expression) ::= (exp ression))| (expression) +

(expression) | (expression}* (expression} | (variable}

(variable} ::= x | у

Зобразити дерево виведення у цій граматиці для ланцюжка (x * у) + x.

Для зручності використаємо позначення E для (expression) (це буде і

початковий символ) та V для (variable).

Тоді правилами перетворення (продукціями граматики будуть)

E ^ (E), E ^ E + E, E ^ E*E та E ^ V з першого виразу, а також V ^ x

та V ^ у з другого виразу.

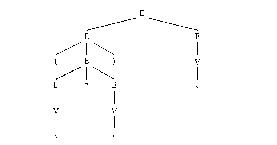
Дерево виведення зображено на рис. 3.

Рис. 3. Дерево виведення для рядка (x * у) + .

3. Література

Нікольський Ю.В., Пасічник В.В., Щербина Ю.М. Дискретна математика: Підручник. - Львів: "Магнолія Плюс”, 2005. - 608с.

3. Завдання

Розв’язати завдання відповідно до свого порядкового номеру у списку групи. Завдання отримати у викладача. При оформленні лабораторної роботи дотримуватись вимог, які наведені в методичних вказівках. Оцінювання виконаної лабораторної роботи проводиться згідно кількості правильно розв’язаних завдань з відповідного варіанту. Завдання лабораторної роботи мають три рівня складності. Оцінювання виконання

11

1. baba

2. abab

3. cbaba

4. bbbcba

Другий рівень Задано множину продукцій у формі Бекуса-Наура: 12 Нехай V = {S,A,B,a,b}, T = {a,b}. Множини продукцій задані нижче a) - j). Визначити, чи є граматика G = (V,T,S,P) граматикою ти­пу 0, але не типу 1; граматикою типу 1, але не типу 2; граматикою типу 2, але не типу 3 або граматикою типу 3: P = {S ^aAB, A ^Bb, B ^Л}; P = {S ^ Aa, A ^ a, A ^ b}; P = {S ^ ABa, AB ^ a}; P = {S ^ ABA, A ^ aB, B ^ ab}; P = {S ^ bA, A ^ B, B ^ a}; P = {S ^ aA, aA ^ B, B ^ aA, A ^ b}; P = {S ^ bA, A ^ b,S ^Л}; P = {S ^ AB, B ^ aAb, aAb ^ b}; P = {S ^ aA, A ^ bB, B ^ b, B ^Л}; P = {S ^ A, A ^ B, B ^Л}. Нехай G - граматика з V = {a,b,c,S}, T = {a,b,c}, початковий символ S і множина продукцій P = {S ^ abS, S ^ bcS, S ^ bbS, S ^ a, S ^ cb} Побудувати дерево виводу для рядків 1 - 3: 1. bcbba

2. bbbcbba

3.bcabbbbbcb

<^E> ^::= (<^E> )|{ E + < E K E *< ^E>K^V> K C

V ::= x | у (C) := 1|2

Вивести ланцюжок. Намалювати дерево виведення.

1. x + (у + у)-у;

2. x + у*(x + x) + у;

3. (^x + ¹)-^.^у + ²)^;

4. x + (у + (x + у));

5. x + x * (x + 2);

6. 2 + x * у + (x +1);

7. x + (x +1 + 2 * x);

8. (2 + x) у + x + у;

9. 1 + (x + у )(x + x);

10. x + (1 + (2 + (x+у)));

11. x* у *(x +1 + у);

12. 2*(x + у +1);

13. ² *( + x-² *(^у + ^у))^;

14. (x + 1)-(x +1)(у +1);

15. у + у + у*(x + x +1);

16. 2*(x + у +1) +1;

17. 2 + 2 *(x + у +1) + x;

18. x+у + (x +1)2;

19. 2 * у + 2 * (x + у) +1;

20. x * у * у + у * (x +1);

1. Паліндромом називається рядок, який однаково читається у прямому і зворотному напрямах. Визначити контекстно вільну граматику, яка породжує всі паліндроми над алфавітом {0,1}.

2. Дано граматику G=(V, T, S, P), де V={0, 1, S, A, B}, T={0,1}, S - початковий символ. Виконати наступні завдання:

• Побудувати мову, породжену такою граматикою.

• Визначити тип граматики.

5.6.1 P = {S ^ 0A, S ^А, S ^ 0, A ^ 1};

13

2. P = {S ^ 101A, A ^ 1A, A ^ 0};

3. P = {S ^ 0A, S ^ 1B, A ^ 0, B ^ 0}

4. P = {S ^ 0A, A ^ 01, S ^ 0B, B ^ 10};

5. P = {S ^ 1S, S ^ 0, S ^ B, B ^ 01};

6. P = {S ^ B01, B ^ 1B, B ^ 0};

7. P = {S ^ 1A, A ^ 1, A ^ 0, S ^ 0};

8. P = {S ^ 111S, S^Л};

9. P = {S ^ 0A, A ^ 01B, S ^ 0B, B ^ 10};

10. P = {S ^ 0S, A ^ A1, S ^ A, A ^Л};

11. P = {S ^ S1, S ^ A, S ^ 1, S ^Л, A ^ 0};

12. P = {S ^ 1A, A ^ 101, S ^ 0B, B ^ 010};

13. P = {S ^ 01A, A ^ 00, S ^ 0B, B ^ 110};

14. P = {S ^ 1A, S ^ 0, S ^Л, B ^ 1, A ^0B};

15. P = {S^0S, S^Л, S^ 1};

16. P = {S ^ 1B, S ^ 0, A ^ 1A, A ^ 0B, A ^ 1, A ^ 0, B ^ 1 };

17. P = {S ^ AB, A ^ 1, S ^ 1A, B ^ 01};

18. P = {S ^ S11, S ^ 0};

19. P = {S^ 10S1, S^Л};

20. P = {S ^ 1B0, B ^ 1B, B ^ 0}.

5.7 Побудувати граматику, яка породжує мову.

1. L(G)={2²ⁿ1, n = 0,1,2,...}

2. L(G) = {2²⁺ⁿ, n = 0, 1, 2, ...}

3. L(G) = {0²”a”⁺², n = 0, 1, 2, ...}

4. L(G) = {2ⁿ1^m+², n, m = 0, 1, 2, ...}

5. L(G) = {2²ⁿ1²ⁿ, n = 0, 1, 2, ...}

6. L(G) = {0ⁿ2^3m, n, m = 0, 1, 2, ...}

7. L(G) = {2²ⁿ1²ⁿ, n = 0, 1, 2, ...}

8. L(G) = {2²ⁿ0^3m, n, m = 0, 1, 2, ...}

9. L(G) = {2³ⁿ0, n = 0, 1, 2, ...}

10. L(G) = {2²ⁿ0ⁿ+², n = 0, 1, 2, ...}

11. L(G) = {2²ⁿ1²ⁿ⁺¹, n = 0, 1, 2, ...}

14