1. Краевые задачи. Классические краевые операторы. Задача Штурма-Лиувилля. Пример: решить задачу ШЛ для y''+λy=0 c краевыми условиями первого рода.

Краевые задачи:

Задача нахождения функции , , из условий

где не все равны 0, называется краевой задачей для ОДУ, и соответственно краевыми условиями (КУ). Замечание: задачу с неоднородными КУ всегда можно свести к задаче с однородными КУ.

Классические краевые операторы: краевой задачи на называются операторы

,

,

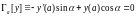При разных значениях α и β классические операторы принимают след вид:

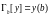1. , - краевые операторы I-ого рода (Дирихле)

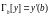2. , - краевые операторы II-ого рода (Неймана)

3. , , - краевые операторы III-ого рода

Задача ШЛ:

Задача нахождения нетривиальных функций y(x) и соответствующих им чисел λ из условий:

-называется задачей ШЛ

Пример Решить задачу Штурма-Лиувилля с краевыми условиями I-го рода:

При λ = µ² > 0 имеем из краевого условия у(0) = 0, что С₂ = 0, => у(x) = С₁ sin(µx). Поэтому из второго краевого условия у(l) = 0 полу­чаем, что µl = πn, откуда имеем бесконечное множество собственных чисел задачи Штурма-Лиувилля: .

Им соответствует бесконечное множество собственных функций:

При λ = -µ² < 0 имеем из краевого условия у(0) = 0, что С₂ = -C₁ => у(х) = 2C₁sh(µx). Поэтому из второго краевого условия у(l) = 0 полу­чаем, что С₁ = 0, те. задача Штурма-Лиувилля не имеет отрицатель­ных собственных чисел.

При λ = 0 имеем из краевого условия у(0) = 0, что С₂ = 0, => у(х) = С₁x. Поэтому из второго краевого условия у(l) = 0 получа­ем, что С₁ = 0, т.е. задача Штурма-Лиувилля не имеет собственного числа, равного нулю.

Итак, мы имеем бесконечное множество нетривиальных решений

,

2. Классическая область определения оператора шл. Симметричность оператора шл.

Отображение, ставящее каждой паре (x₁; x₂) элементов линейного пространства V число, обозначаемое (x₁; x₂) (действительное или комплексное), называется скалярным произведением, если

1. , причем <=> x=0;

2. (x₁,x₂)= (x₂,x₁)

3. 

4. , .

Нормой элемента x линейного пространства V , порождённой скалярным произведением (x1; x2), называется число, обозначаемое и равное корню из его скалярного квадрата:

_{Скалярное произведение} в

_{Классическая область определения}:

Основной дифференциальный оператор: ,

Оператор ШЛ:оператор на D(L) и обозн L[y]

Симметричность оператора ШЛ:

Лемма: Пусть f(x); g(x) – функции класса

Тогда справедливы равенства

_{где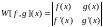 -определитель Вронского}

_{Док: для первого равенства рассмотрим 3 случая}

1. . Тогда f(a)=g(a)=0, и равенство очевидно

2. . Тогда f'(a)=g'(a)=0, и равенство очевидно

3. .Тогда f'(a)=hf(a), g'(a)=hg(a) и равенство тоже выполняется

Симметричность оператора ШЛ:

Оператор L[y] является симметричным , т.е.– функций класса справедливо равенство

док-во: =[дважды по частям]=

3. Действительность собственных значений оператора шл

Все собственные значения задачи Штурма–Лиувилля действительны.

Док: Пусть – собственное значение задачи Штурма–Лиувилля и, соответственно, оператора Штурма–Лиувилля L[y]. Пусть y(x) = u(x)+iv(x) – соответствующая собственная функция. Тогда 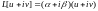, что равносильно системе

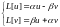=> равны между собой

, что означает, что , а значит

4. Ортогональность собственных функций оператора шл.

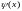Пусть и – собственные функции задачи

Штурма–Лиувилля, соответствующие разным собственным значениям

, соответственно:

Тогда и ортогональны в смысле скалярного произведения

док: Напомним, что все линейно независимые собственные функции задачи

Штурма–Лиувилля могут быть выражены через действительнозначные

собственные функции, и мы для удобства ими и ограничиваемся.

Пусть

= = =[ в силу симметричности L]= = =

Отсюда тогда

5. Простота собственных значений оператора шл

Пусть и – собственные функции задачи

Штурма–Лиувилля, соответствующие одному и тому же значению , тогда и линейно зависимы на

Док: Лемма билета 2 утвержает – функции класса т.е. удовлетворяющих классическим краевым условиям на концах , справедливы равенства:

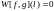и , где

Как известно из общей теории линейных ОДУ n-го порядка, если определитель Вронского системы решений одного и того же линейного уравнения равен нулю хотя бы в одной точке, то он равен нулю на всём промежутке, на котором выполняется уравнение (в нашем случае это ), и следовательно сами функции и линейно зависимы на этом промежутке.

Замечание Доказанное свойство называется простотой собственных значений задачи Штурма–Лиувилля и означает, что кратность каждого собственного значения равна 1.

6. Теорема Стеклова. Пример: разложить функцию в ряд по собственным функциям задачи шл.

Пусть и удовлетворяет КУ: ,

Пусть – ортогональная система всех линейно независимых

собственных функций задачи Штурма–Лиувилля:

Тогда справедливо представление функции f(x) в виде ряда (Фурье):

, , причем ряд сходится абсолютно и равномерно на всем

Пример: Пусть дана задача ШЛ:

Тогда, решив её как мы сделали в примере 1. 3 (с. 6), получим систему

собственных функций:

, , ,

Посчитав норму собственных функций:

,

получим представление для f(x): ,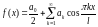

что совпадает с формулой разложения f(x) в тригонометрический ряд Фурье по косинусам.

Для получим тригонометрический ряд Фурье по синусам:

, .