36.Спин-орбит0е в/з-е. Тонкая структура. При решении Уравнения Шрёдингера для электрона с точностью до членов ( – скорость движения электрона) можно найти релятивистскую поправку к оператору Гамильтона , включающую в себя:

– поправку, введенную Дарвином и определяющую дополнительную энергию взаимодействия электрона с ядром в –состояниях (ее называют иногда оператором контактного взаимодействия);

– поправку к оператору кинетической энергии, возникающую из-за зависимости энергии частицы от ее импульса;

– поправку, называемую оператором спин-орбитального взаимодействия.

После учета этих операторов в гамильтониане решение уравнения для функции методом последовательных приближений позволяет найти поправку и энергию стационарного состояния:

. (11.14)

Из формулы (11.14) следует, что теперь, кроме главного квантового числа , энергию уровня определяет еще и квантовое число , то есть в результате учета спин-орбитального взаимодействия и релятивистских эффектов снимается вырождение уровней по квантовому числу . Для электрона, в соответствии с формулой (6.34), возможны значения и , где s = 1/2 – спиновое квантовое число электрона. При этом значения орбитального квантового числа определяются следующим образом: . Снятие вырождения проявляется как расщепление энергетических уровней на подуровни, что приводит к расщеплению спектральных линий на компоненты, обусловливая их тонкую структуру.

Поскольку энергия уровня не зависит от орбитального квантового числа , (см. (11.14)), пары уровней, имеющие одинаковые и , при остаются вырожденными. Система уровней, соответствующая разным значениям при одинаковом значении , называется тонкой структурой. Величина называется постоянной тонкой структуры.

35.Периодич. с-ма эл-ов.Правило Клечковского. Основными принципами, лежащими в основе заполнения спин-орбиталей, являются следующие:

1. В каждом квантовом состоянии атома не может быть более одного электрона (принцип Паули);

2. При дополнении электронной оболочки каждым последующим электроном получаемая при этом атомная система должна обладать минимальной энергией.

Советский ученый В.М. Клечковский установил эмпирическое правило, позволяющее расположить электронные оболочки (состояния с заданными значениями и ) в сложном атоме в порядке возрастания энергии, то есть установить последовательность их заполнения. Правило Клечковского гласит: заполнение оболочек электронами происходит в порядке возрастания величины , причем состояния с одинаковым значением этой суммы заполняются, как правило, в порядке возрастания .

В таблице 12.3 видно, что в пределах от 1 - до 3 -состояния энергия растет с ростом , а затем эта последовательность состояний нарушается: состояние 4 оказывается энергетически более выгодным, чем состояние 3 . Аналогично взаимное расположение любых - и -состояний.

Как показано выше, каждая электронная оболочка содержит квантовых состояний.

Суммарный спиновый момент нескольких электронов определяется взаимной ориентацией спиновых моментов отдельных электронов. Спиновый момент каждого отдельного электрона может иметь положительную ( ) или отрицательную ( ) проекцию на заданное направление. Максимальное значение суммарного спинового момента, таким образом, будет реализовано, если проекции спинов электронов имеют одинаковые знаки. Однако все электроны заданной оболочки, если заполнено более ее половины, не могут иметь одинаковые значения квантового числа , так как при заполнении оболочки электронами необходимо выполнение принципа Паули. Например, имеющиеся в -оболочке шесть состояний (формула 12.1) заполняются в следующем порядке: первые три электрона оказываются в состояниях с и спином , , ; последующие три – в состояниях с и спином , , . Состояния, отличающиеся только значениями магнитного квантового числа , в отсутствие магнитных взаимодействий изоэнергетичны, то есть имеет место вырождение по .

Пользуясь рассмотренными выше правилами можно описать электронную структуру атома в нормальном (с наименьшей энергией) состоянии для любого -го элемента Периодической системы элементов Д.И. Менделеева. Достаточно записать для электронов электронные оболочки (или спин-орбитали) в порядке возрастания их энергии.

В спектроскопии принята более компактная запись электронной структуры, называемая электронной конфигурацией. Электронная конфигурация – это запись, указывающая количество электронов на каждой электронной оболочке атома в порядке возрастания их энергии. Например, электронная конфигурация атома натрия ( ) в нормальном состоянии имеет вид . Электроны полностью заполненных внутренних оболочек ( – для ) совместно с ядром образуют остов, в поле которого движется внешний ( ) электрон. Электроны внешних оболочек, называются валентными или оптическими, так как именно их состояниями определяются и химические свойства, и структура оптических спектров атомов.

При поглощении энергии извне (например, энергии внешнего электромагнитного излучения) атом переходит в состояние с большей энергией (в возбужденное состояние). На структурном уровне это означает, что один или несколько оптических электронов переходят в более высокоэнергетическое состояние. Образовавшаяся при этом электронная структура атома описывается электронной конфигурацией возбужденного состояния. Например, если в результате возбуждения оптический электрон в атоме натрия перешел из - в -состояние, то электронная конфигурация возбужденного состояния натрия примет вид .

37.Типы связи эл-ов в сложном атоме. Терм атома. В сложных атомах можно выделить два основных вида взаимодействия между моментами отдельных электронов:

– межэлектронное взаимодействие – взаимодействие магнитных орбитальных моментов различных электронов между собой и отдельно взаимодействие спиновых магнитных моментов различных электронов между собой;

– спин-орбитальное взаимодействие – взаимодействие спинового и орбитального магнитных моментов каждого отдельно взятого электрона.

При нахождении полного момента атома в первую очередь необходимо учесть более существенное из названных взаимодействий, а затем – менее существенное. В зависимости от того, какое из двух указанных взаимодействий является превалирующим, выделяются две логические схемы нахождения полного магнитного момента (и, следовательно, полного момента импульса) атома, иначе говоря, – два типа связи электронов в атоме: и .

Связь (или нормальная, или связь Рассел-Саундерса) имеет место, если пренебречь спин-орбитальным взаимодействием. Такое допущение вполне разумно для атомов начала и середины Периодической системы Д.И. Менделеева. В этом случае интегралами движения, то есть физическими величинами, характеризующими стационарное состояние атома, являются: суммарный орбитальный момент атома , суммарный спиновый момент атома и их проекции и . Поэтому состояние атома можно описать, задавая значения четырех квантовых чисел: . Энергия атома в этом приближении зависит от значений квантовых чисел и . Таким образом, оказывается, что в отсутствие спин-орбитального взаимодействия каждый энергетический уровень атома с заданными значениями и имеет кратность вырождения . Совокупность состояний атома, соответствующих заданным значениям и , называется термом атома. Очевидно, что терм атома характеризует (в отсутствие спин-орбитального взаимодействия) определенный атомный энергетический уровень.

38.Основное и возбуждённое состояние сложного атома.Правила Хунда.Незначительное по величине спин-орбитальное взаимодействие можно рассматривать как поправку (возмущение) к гамильтониану. В результате этого возмущения происходит снятие вырождения (то есть расщепление) энергетического уровня по квантовому числу . Таким образом, для характеристики энергетического уровня атома необходимо указать значения трех квантовых чисел .

В спектроскопии принята следующая схема обозначения электронных состояний атома: записывается буквенное обозначение квантового числа ; в качестве нижнего индекса справа указывается значение , а в качестве верхнего индекса слева – значение величины , называемой спиновой мультиплетностью. Например, обозначение относится к энергетическому уровню с .

Используя изложенные выше общие положения, рассмотрим процедуру определения термов на примере атома углерода, имеющего в основном состоянии электронную конфигурацию . Для решения этой задачи необходимо определить возможные для данного атома значения и . Учтем, что суммарные моменты полностью заполненных оболочек равны нулю. Тогда в качестве исходных, определяющих термы атома углерода, достаточно рассматривать два -электрона, для которых ; ; ; ; .

Общая логическая схема определения полного момента атома при -связи представляется следующими тремя уравнениями:

, , .

Для рассматриваемого примера (атом углерода)

; .

В соответствии с квантовомеханической теорией сложения моментов, абсолютные величины суммарных моментов определяются значениями квантовых чисел и , которые находятся следующим образом:

, , , …, ;

, , , …, .

Квантовые числа и определяются из соотношений

; .

При этом необходимо исключить из рассмотрения те комбинации квантовых чисел, которые запрещены принципом Паули. Все возможные значения и проще всего получить с помощью схемы, аналог которой для атома углерода (для него ; 1, 0; 0) представлен на рисунке 13.1. Заштрихованные клетки на схеме соответствуют состояниям, запрещенным принципом Паули.

Теперь из полученных состояний выберем те, которые соответствуют определенному значению . При этом учтем, что . В нашем случае = 2. Выписываем все состояний, отвечающих . Они лежат на диагонали (для них ):

Полученный уровень (терм) называется синглетным, так как .

Затем из оставшихся состояний снова выбираем состояние с наибольшим значением : ( ). Ему соответствуют значения . Таким образом, получаем еще состояний, которым на рисунке 13.1 соответствуют клетки с диагоналями :

Этот уровень (терм) называется триплетным, поскольку .

Осталось еще одно состояние, соответствующее диагонали на рисунке 6.1:

Это – также синглетный терм ( =1).

Возмущающее спин-орбитальное взаимодействие приводит к снятию вырождения по тех уровней, мультиплетность которых отлична от единицы.

Определим для триплетного уровня возможные значения . Так как общее правило определяет возможность существования состояний с , то для рассматриваемого случая имеем: 1, 0 .

Таким образом, триплетный уровень вследствие спин-орбитального взаимодействия расщепляется на три компонента, которым соответствуют спектроскопические обозначения

, , .

Для синглетных уровней ( ) значение совпадает со значением соответствующего этому терму ; спектроскопические обозначения соответствующих этим уровням термов имеют вид , .

Чтобы получить схему энергетических уровней атома, необходимо полученные состояния расположить в порядке возрастания энергии. Согласно эмпирическим правилам Хунда энергия уровня будет наименьшей, если:

1. квантовое число максимально;

2. при равных максимально квантовое число ;

3. при равных и квантовое число 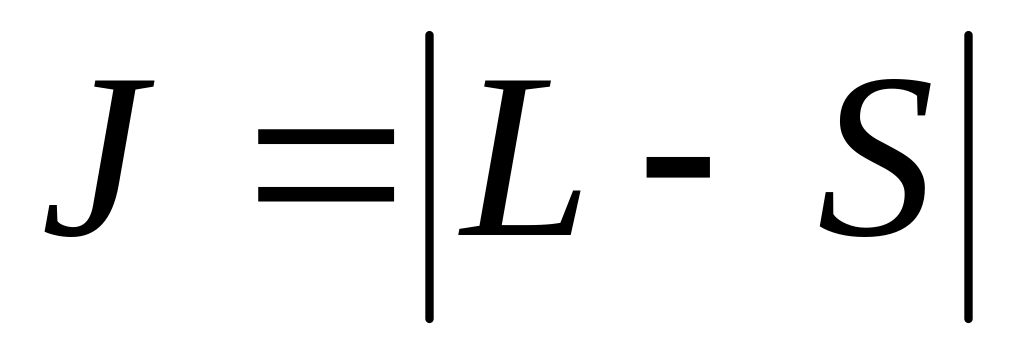(при заполнении электронами не более половины оболочки) и 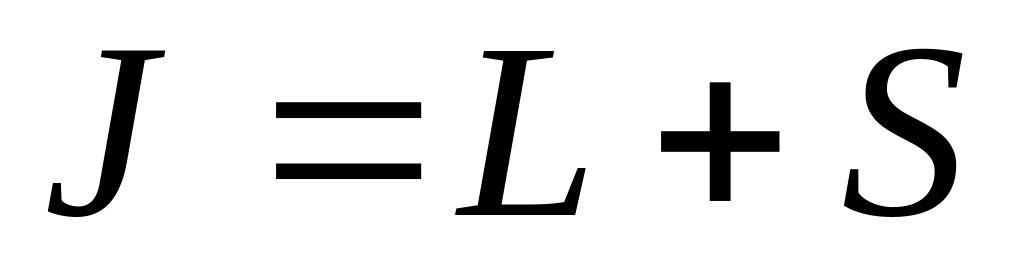(в остальных случаях).

Из правила Хунда нет исключений при определении основного состояния атома, но оно часто нарушается для возбуждённых состояний.

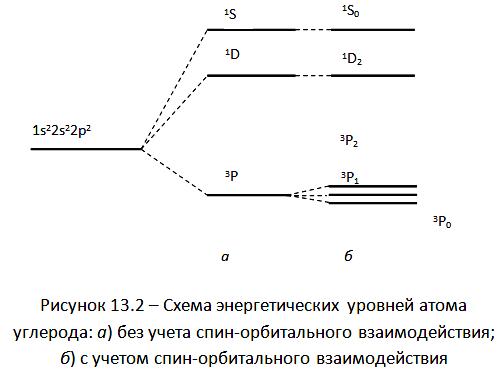
Воспользовавшись правилами Хунда, построим схему энергетических уровней атома углерода, соответствующую электронной конфигурации (рисунок 13.2).

В атомах возможны и другие типы связи. Какая из возможных связей осуществляется фактически, зависит от характера взаимодействия между электронами. Если энергия взаимодействия спинового магнитного момента электрона с его орбитальным магнитным моментом больше энергии взаимодействия орбитального и спинового магнитных моментов электрона с соответствующими моментами других электронов, то осуществляется -связь. Полный момент атома при этом типе связи определяется в соответствии со следующим алгоритмом:

; .

В этом случае энергия уровня уже не определяется значениями квантовых чисел и , так как соответствующие им моменты не являются интегралами движения. Вместо них для описания состояния используются квантовое число атома и j_i отдельных электронов.

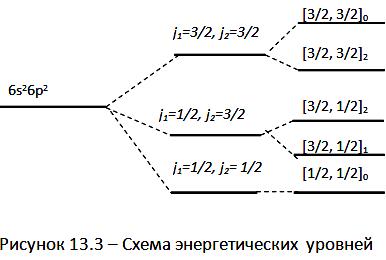
При одинаковой электронной конфигурации внешней оболочки легких и тяжелых атомов логическая схема определения полного момента для них различна. Различается и взаимное расположение их энергетических уровней. В качестве иллюстрации на рисунке 13.3 приведена схема энергетических уровней атома свинца (электронная конфигурация основного состояния – … ), в котором реализуется -связь.

Рассмотренные ( )- и ( )-связь являются предельными типами связи электронов в атоме. Для каждого конкретного атома порядок определения полного момента устанавливается с учетом соотношения энергий межэлектронного и спин-орбитального взаимодействий для различных групп электронов.

39.Осцилляторы эл.маг. поля и фотоны. В состоянии равновесия число переходов, совершаемых с поглощением энергии, равно числу переходов, совершаемых системой атомов (молекул) за это же время с излучением энергии (условие детального равновесия):

.

Установим, какими физическими параметрами частиц определяются значения коэффициентов Эйнштейна, соответствующие электрическим дипольным переходам. Для этого воспользуемся принципом соответствия, рассматривая свойства атомов и молекул на основе квантового, а свойства электромагнитного излучения – на основе классического описания. Отметим, что такой подход вполне оправдан и сделанные на его основе выводы подтверждены экспериментально.

В классической теории получена следующая формула средней мощности излучения классического осциллятора (величины энергии, испускаемой осциллятором в единицу времени):

(20.13)

где – амплитуда электрического дипольного момента осциллятора, – круговая частота испускаемого электромагнитного излучения, – скорость света в вакууме.

Учтём, что в нашем рассмотрении , и воспользуемся принципом соответствия результатов квантовой и классической теории, в соответствии с которым ( – матричный элемент дипольного момента спонтанного излучательного перехода ), и запишем формулу (20.13) в виде:

. (20.14)

Далее воспользуемся формулой (20.6) и выразим энергию излучения, испускаемого за единицу времени одной частицей спонтанно (что соответствует одному осциллятору в классической модели):

(20.15)

Приравнивая правые части равенств (20.14) и (20.15), выразим коэффициент Эйнштейна , имеющий смысл вероятности спонтанного испускания кванта одной частицей за единицу времени:

(20.16)

Воспользуемся формулой (20.11) и получим выражения для коэффициентов Эйнштейна и :

, .

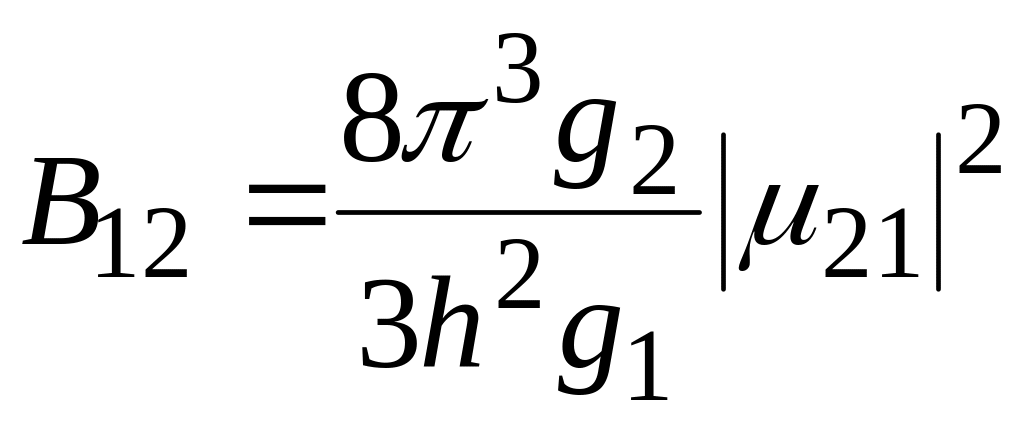Таким образом, коэффициенты Эйнштейна непосредственно связаны с фундаментальными параметрами частиц, какими являются матричные элементы дипольного момента квантовых переходов .В квантовой механике значение матричного элемента дипольного момента определяется в соответствии с формулой:

(20.17)

где х – совокупность всех координат соответствующей формы движения; – оператор электрического дипольного момента; – волновые функции, соответствующие исходному и конечному состоянию системы.

40.Вероятности переходов между состояниями атома. Коэфф-ты Эйнштейна. В отсутствие внешних воздействий квантовая система (например, атом) находится в стационарном состоянии с наименьшей энергией – нормальном состоянии. Передавая системе энергию извне, её можно перевести в одно из стационарных возбужденных состояний.

Квантовые переходы атомной системы из одного стационарного состояния в другое обусловлены получением извне или передачей энергии этой системой другим объектам или ее излучением в окружающее атом пространство. Переходы, при которых атомная система поглощает, испускает или рассеивает электромагнитное излучение, называются радиационными (или излучательными). Каждому радиационному переходу между энергетическими уровнями и в спектре соответствует спектральная линия, характеризующаяся частотой и некоторой энергетической характеристикой излучения, испущенного (для спектров испускания), поглощенного (для спектров поглощения) или рассеянного (для спектров рассеяния) атомной системой. Переходы, при которых происходит непосредственный обмен энергией данной атомной системы с другими атомными системами (столкновения, химическая реакция и т. д.), называются нерадиационными (или безызлучательными).

Квантовые переходы характеризуют коэффициентами Эйнштейна , физический смысл которых поясним позже.

Проанализируем, какими внутренними характеристиками атомной системы определяется интенсивность спектральной линии. Рассмотрение проведем для простейшей – двухуровневой системы (рисунок 19.1). Пусть и – два энергетических уровня изолированной атомной системы (атома или молекулы), населенность которых соответственно обозначим N₁ и N₂ . Число частиц в единице объема, совершающих за время dt при стационарном режиме возбуждения переходы , сопровождающиеся поглощением энергии электромагнитного излучения, определим в соответствии с формулой:

(20.2)

где – объемная спектральная плотность энергии внешнего (возбуждающего) излучения, частота которого . При этом частицами, переведенными в возбужденное состояние с энергией в единичном объеме вещества, поглощается энергия

. (20.3) Из выражения (20.2) видно, что

(20.4)

– это вероятность перехода за единицу времени, сопровождающегося поглощением, в расчете на одну частицу. Таким образом, коэффициент Эйнштейна имеет вероятностный (статистический) смысл.

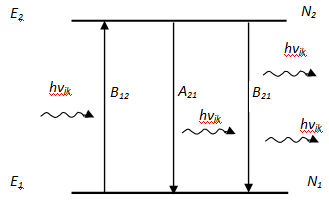
Рис. 20.1-Разновидности радиоц-ых переходов частиц в простейшей 2-уровневой с-ме.

Процесс испускания электромагнитного излучения может происходить в соответствии с двумя механизмами: спонтанно (вследствие внутренних причин) и вынужденно (при воздействии возбуждающего излучения).

Общее число частиц, совершающих за время dt спонтанные переходы , прямо пропорциональна населенности уровня, соответствующего исходному состоянию системы:

. (20.5)

Энергию электромагнитного излучения, спонтанно испущенного атомами (молекулами), находящимися в единичном объеме вещества, за время , можно представить в виде:

. (20.6)

Из формулы (20.5) выразим величину :

(20.7)

– коэффициент Эйнштейна, имеющий смысл вероятности перехода, сопровождающегося спонтанным испусканием электромагнитного излучения одной частицей за единицу времени.

Вынужденное испускание происходит под действием внешнего (вынуждающего) излучения. Число вынужденных излучательных переходов за время dt в рассматриваемой системе уровней прямо пропорционально населенности N₂ уровня, соответствующего исходному состоянию системы (E₂) и объемной спектральной плотности энергии внешнего (возбуждающего) излучения u₁₂:

(20.8)

Энергия вынужденного излучения, испущенного в единичном объеме вещества за время dt, запишем в виде:

(20.9)

Из формулы (20.8) легко выделить величину

(20.10)

– вероятность перехода, совершаемого одной частицей за единицу времени и сопровождающегося вынужденным испусканием. Здесь – коэффициент Эйнштейна для вынужденных излучательных переходов.

Существенно, что на основе изложенных представлений в 1916 году Эйнштейном строго и изящно была выведена формула Планка для объемной спектральной плотности энергии теплового излучения, частота которого v, при заданной температуре T:

,

а также установлены соотношения между коэффициентами Эйнштейна, для рассматриваемых переходов имеющие вид:

(20.11)

где и – статистические веса энергетических уровней и .

Таким образом, внутренними параметрами атомной системы, определяющими энергию электромагнитного излучения, поглощённого или испущенного веществом, и, следовательно, – интенсивность спектральных линий в регистрируемом спектре, являются вероятности переходов в единицу времени, то есть коэффициенты Эйнштейна.

Используя формулы (20.7), (20.10) и (20.11), можно выразить полную вероятность испускания:

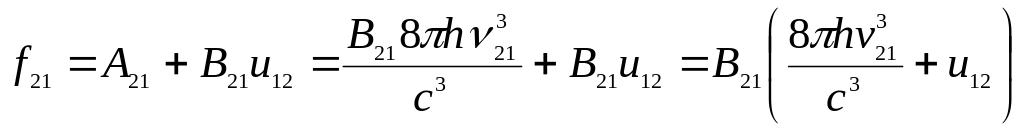(20.12)

Анализируя формулу (20.12), видим, что при относительно невысоких значениях объемной плотности возбуждающего излучения вероятность f₂₁ практически полностью определяется вероятностью спонтанных переходов с испусканием энергии. При высокой мощности облучения вероятность вынужденного испускания может стать существенно выше вероятности спонтанного испускания. Такая ситуация имеет место в активной среде генерирующего лазера, а также при использовании лазера в качестве источника возбуждающего излучения.

Выражение используется для определения правил отбора. Функции состояния и зависят от квантовых чисел как от параметров. Правила отбора – это условия для изменения значений квантовых чисел в результате перехода, при которых вероятность излучательного квантового перехода, и, следовательно, матричный элемент перехода, отличны от нуля. Такие переходы называются разрешенными. Переходы, вероятность которых равна нулю, называются запрещенными. Например, правила отбора для переходов в водородоподобной атомной системе имеют вид:

любое целочисленное значение ( – главное квантовое число),

( – орбитальное квантовое число),

( – магнитное квантовое число),

( – спиновое квантовое число).

41.УШ для атовов щелоч. Ме и его реш-е на основе эффективного ядра. Электроны внутренних оболочек с общим отрицательным зарядом вместе с ядром, положительный заряд которого , образуют устойчивый «остов» атома с суммарным зарядом . В поле этого остова, называемого также эффективным ядром, движется валентный (оптический) -электрон.

Рассматривая остов как сложную объемную систему с суммарным зарядом , потенциальную энергию валентного электрона в поле эффективного ядра можно представить в виде ряда

, (14.1)

первый член которого учитывает кулоновское взаимодействие электронов с ядром; сохранение в (14.1) двух первых членов соответствует так называемому дипольному приближению, трех первых членов – квадрупольному приближению.

Ограничиваясь в первом приближении двумя первыми членами разложения (14.1) и преобразуя уравнение Шредингера аналогично тому, как это было сделано для атома водорода, получим для угловой функции уравнение, полностью совпадающее с (10.4), а уравнение для радиальной функции запишем в виде

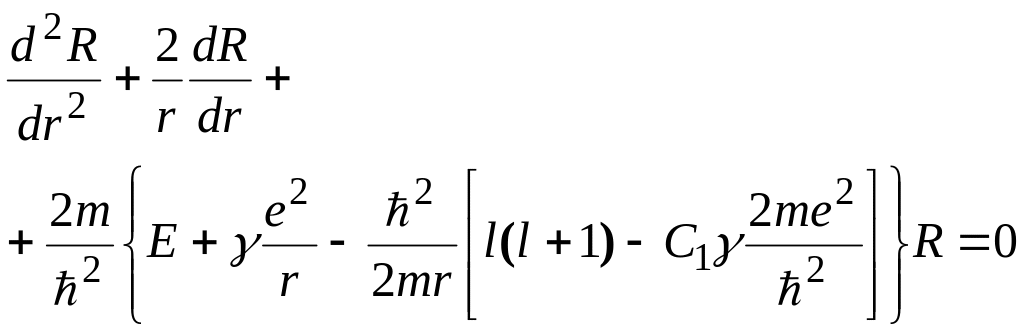(14.2)

Сравнивая (10.13) и (14.2), видим, что выражение для потенциальной энергии содержит дополнительный член , появившийся в результате учета второго слагаемого в уравнении (14.1). Уравнения (10.13) и (14.2) формально тождественны, если положить в (14.2)

. (14.3)

Разрешив уравнение (14.3) относительно , получим:

. (14.4)