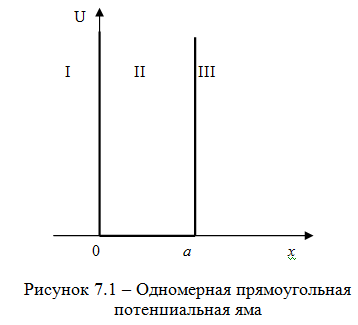
19.Решение УШ для частицы нах-ся в одномерн. бескон. глубокой потец. яме Пусть одномерная бесконечно глубокая потенциальная яма имеет ширину и заключена в интервале (рисунок 7.1). Поле потенциальных сил таково, что

при (область П)

при < 0 (область I) и при > (область Ш).

Найдем волновые функции и значения энергии, отвечающие возможным состояниям частицы в рассматриваемом потенциальном поле. Для этого найдем решения одномерного стационарного уравнения Шрёдингера

(7.1)

в каждой из трёх областей пространства.

Проведем анализ уравнения (7.1) в областях одномерного пространства I и III, в пределах которых . Для этого запишем (7.1) в виде:

.

Видим, что это равенство выполняется только при условии . Это означает, что частица не может выйти за пределы области пространства II, то есть за пределы потенциальной ямы, поскольку вероятность нахождения частицы вне ямы равна нулю.

Вследствие того, что волновая функция непрерывна на границах областей с разными значениями потенциальной энергии, справедливы равенства:

и . (7.2)

Уравнения (7.2) выражают граничные условия.

Запишем уравнение (7.1) для области пространства II, обозначив функцию состояния в этой области .

,

или

, (7.3)

где

. (7.4)

Общим решением уравнения (7.3) является функция

. (7.5)

Проанализируем (7.5), воспользовавшись граничными условиями (7.2). Из условия следует, что , из условия вытекает, чт , (7.6)

и при из (7.6) получаем, что и, следовательно,

. (7.7)

Так как и , то и : , 2, 3…

Таким образом, решение уравнения Шредингера в области II имеет вид:

. (7.8)

Сопоставляя выражения (7.4) и (7.7), найдем возможные значения энергии частицы:

; 1, 2, 3 (7.9)

Выражение (7.9) является условием квантования энергии частицы. Из него следует, что существует некоторая минимальная энергия, не равная нулю:

; (7.10)

она соответствует основному состоянию движения частиц. Волновая функция этого состояния, как следует из (7.8),

(7.11)

ни в какой точке внутри ямы в нуль не обращается; она может быть равной нулю лишь на границах ямы.

Из (7.10) видно, что с уменьшением ширины ямы минимальная энергия растет. Следовательно, уменьшение пространства локализации частиц неизбежно сопровождается возрастанием их энергии. Это одно из проявлений принципа неопределенностей.

С учетом того, что частица может находиться лишь внутри ямы, условие нормировки волновой функции примет вид:

или, с учетом (7.8),

.

Из этого условия найдем нормирующий множитель: .

Таким образом, волновая функция имеет вид:

. (7.12)

Выражение (7.12) представляет систему собственных функций, соответствующих возможным состояниям частицы в бесконечно глубокой потенциальной яме. Эти функции обращаются в нуль, , как на границах потенциальной ямы, так и в узловых точках внутри нее, значения координаты которых определяются из условия .

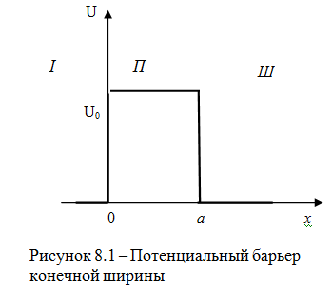
20.Прох-е частицей прямоуг. одном. потец. барьера В областях и III потенциальная энергия равна нулю: (  0) = 0.

В области (0 < < ) потенциальная энергия = .

Именно эта область является потенциальным барьером.

Состояние движения частицы характеризуется коэффициентами отражения и прохождения , которые имеют смысл вероятности того, что частица останется в области пространства I (коэффициент R) или перейдет в область Ш (коэффициент D).

Рассмотрим случай, когда < , и найдем для частицы коэффициенты отражения и прохождения . Для этого необходимо решить одномерное стационарное уравнение Шрёдингера и найти функции состояния , и в каждой из областей пространства , , .

(   ) = 0.

Уравнение Шрёдингера для областей , , соответственно имеет вид:

;

, ; (8.1)

, .

Решение уравнения для области имеет вид

, (8.2)

и описывает падающую волну де Бройля с амплитудой и отраженную волну с амплитудой . Решение в области III содержит только прошедшую волну, распространяющуюся в положительном направлении оси :

. (8.3)

В области П общее решение уравнения Шрёдингера имеет вид

. (8.4)

21.Прозрачность потец. Барьера произ-ой формы. Если потенциальный барьер имеет произвольную форму (рисунок 8.2), то его можно представить как последовательность прямоугольных потенциальных ба

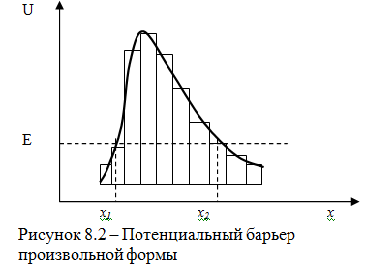рьеров. Коэффициент прохождения такого барьера в этом случае приблизительно равен произведению коэффициентов прохождения через все прямоугольные потенциальные барьеры, которыми он моделируется. Числовой множитель перед экспонентой в (8.15) при плавном изменении потенциальной энергии является медленно меняющейся функцией. Таким образом, для потенциального барьера произвольной формы коэффициент прозрачности определяется

. (8.16)

Описанные в данном разделе особенности поведения частиц связаны с их корпускулярно-волновой природой. Туннельный эффект существен лишь для

систем, имеющих микроскопические размеры и массы. Чем уже потенциальный барьер и чем меньше разность , тем больше вероятность прохождения частицы через барьер.

22. Тунельный эфф-т. Холодная эмиссия элект. Преодоление микрочастицей потенциального барьера в случае, когда ее полная энергия меньше высоты барьера, называется туннельным эффектом, или туннелированием. Примером проявления туннельного эффекта в атомной физике могут служить автоионизация атома в сильном электрическом поле и ионизация атома в поле сильной электромагнитной волны.

Туннельный эффект лежит в основе альфа-распада радиоактивных ядер. Без туннельного эффекта было бы невозможно протекание термоядерных реакций: кулоновский потенциальный барьер, препятствующий необходимому для синтеза сближению ядер-реагентов, преодолевается частично благодаря высокой скорости (высокой температуре) таких ядер, а частично - благодаря туннельному эффекту.

Особенно многочисленны проявления туннельного эффекта в физике твердого тела. Туннельным эффектом объясняется холодная эмиссия электронов из металла. Электроны удерживаются внутри металла силами притяжения, и для удаления электрона из металла необходимо совершить определенную работу. Это означает, что потенциальная энергия электрона вне металла больше, чем внутри него, причем на границе металл – вакуум потенциальная энергия резко возрастает. Если вблизи поверхности металла создано электрическое поле с напряженностью порядка 10⁸ В/м, электроны покидают поверхность металла. Это явление называется холодной эмиссией.

Классическая физика не может объяснить это явление: электрическое поле в металл не проникает и изменяет потенциальную энергию лишь вне металла (штриховая линия на рисунке 8.3). Чтобы покинуть металл, электроны должны преодолеть потенциальный барьер.

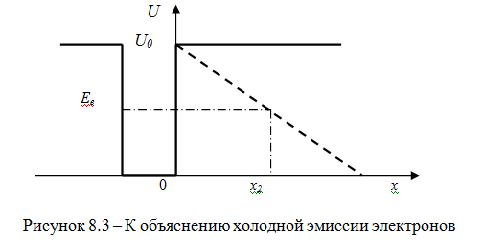
Поскольку их энергия меньше высоты барьера , то с классической точки зрения электроны не могут выйти за пределы поверхности. В соответствии с квантовой механикой коэффициент прохождения электронов через барьер определяется интегралом

здесь (где – напряженность электрического поля), ), Тогда значение интеграла определяется следующим образом:

,

где В/м. Так как ток эмиссии пропорционален коэффициенту прохождения барьера, то в соответствии с формулой (8.16) зависимость плотности тока эмиссии от напряженности электрического поля должна иметь вид:

.Такая зависимость хорошо подтверждается экспериментом.

23. Средние знач-я и опер-ры физ величин. Т.к. квантовомеханическое описание состояния частицы носит статистический (вероятностный) характер, особое значение имеют средние значения физических величин. Рассмотрим правила определения средних значений и явного вида операторов физических величин, которые необходимы для описания состояний электрона в атоме и атомной системы как целого.

Среднее значение величины из достаточно большого числа измерений определяется следующим образом:

. (6.1)

В теории вероятностей среднее значение величины , принимающей значения ( 1, 2, 3, …) с вероятностями , находят по формуле

(6.2)

Как было указано выше (смотри формулу (5.6), стационарное состояние частицы в квантовой механике описывается функцией . То есть плотность вероятности обнаружить частицу в окрестности точки определяется ее координатной частью:

.

Воспользуемся формулой (6.2) и определим среднее значение координаты частицы в одномерном случае.

.

Учитывая, что при квантово-механическом описании координате , а также ее функциям сопоставляется оператор умножения ( и ,соответственно), можно записать, переходя к пределу,

. (6.3)

Этот результат можно обобщить на случай многомерного пространства:

, (6.4)

где – элементарный объем в – мерном пространстве.

Среднее значение физической величины, являющейся функцией координат, определяется аналогичным образом

. (6.5)

По аналогии с (6.3) запишем формулу для определения среднего значения импульса частицы в одномерном пространстве:

, (6.6)

где – плотность вероятности того, что частица имеет значение проекции импульса , а интегрирование проводится по всему импульсному пространству. Но поскольку функция нам неизвестна, необходимо перейти от импульсного пространства к координатному, в котором плотность вероятности определяется функцией состояния, являющейся решением известного нам уравнения Шредингера. Для этого воспользуемся преобразованием Фурье, и выражение (6.6) примет вид:

, (6.7)

Где (6.8)

– оператор импульса частицы в одномерном пространстве.

– оператор функции ,

– элементарный объем в -мерном пространстве.

Это правило может быть обобщено: среднее значение физической величины, представленной оператором , в состоянии, характеризуемом функцией , определяется формулой

. (6.10)

Таким образом, для вычисления среднего значения физической величины достаточно знать -функцию состояния частицы и явный вид изображающего эту величину оператора.

Воспользуемся формулой (6.8) и, перейдя к трехмерному пространству, найдем, что

, ,

и оператор импульса в трехмерном пространстве имеет вид:

, (6.11)

где , , – орты декартовой системы координат.

Определим вид оператора Гамильтона . В классической физике функцией Гамильтона называется функция полной энергии, выраженная через импульсы и координаты частиц. Для частицы массы в нерелятивистском приближении полная энергия равна сумме кинетической и потенциальной энергий:

. (6.12)

В квантовой механике функции Гамильтона должен соответствовать оператор, вид которого определяется в соответствии с постулатом 7 (смотри лекцию 5) следующим образом:

. (6.13)

После подстановки в (6.13) вместо импульса его оператора (6.11), получим:

. (6.14)

Явный вид оператора Гамильтона зависит от решаемой задачи, содержание которой конкретизирует вид функции .

Наряду с энергией важнейшей характеристикой движения электрона относительно ядра в атоме является орбитальный момента импульса. В классической механике момент импульса частицы определяется как векторное произведение радиус-вектора частицы на ее импульс :

,или в проекциях на оси координат:

В квантовой механике проекциям момента импульса , , ставятся в соответствие операторы

(6.15)

В сферических координатах выражениям (6.15) соответствуют

24. Ур-е для опред-я собств-го сост-ия опер-ра физ. велечины. Собственные функции оператора определяются из уравнения

и имеют вид:

. (6.17)

Из требования однозначности функции следует, что она должна быть периодической с периодом . Тогда

, 0, , , … . (6.18)

Для операторов выполняются следующие перестановочные (коммутационные) соотношения:

; ; , (6.19)

из которых следует, что проекции орбитального момента связаны соотношениями неопределенностей вида

,

где и  неопределенности (дисперсии) измеряемых значений физических величин и .

Для оператора

(6.20)

с учетом формулы (6.16) можно получить выражение

, (6.21)

в котором

(6.22)

 оператор Лежандра.

Несложно убедиться, что оператор коммутирует с каждым из операторов :

; , , . (6.23)