4. Задача об оптимальном управлении как задача Майера. Принцип максимума Понтрягина. Особенности применения принципа максимума.

1. Задача об оптимальном управлении как задача Майера.

Развитие систем управления было связано с повышением требований по точности, быстродействию, надежности с одновременным уменьшением габаритов, весов, ресурсов. Для их создания потребовался аппарат вариационного исчисления. Но здесь возникли трудности:

• и з-за ограничений на управление мощность, механические ограничения по повороту), оптимальные управления оказались кусочно-непрерывными функциями с точками разрыва 1-го рода, число которых неизвестно.

Это противоречило предположению классического вариационного исчисления о непрерывности экстремалей.

Поэтому начались работы по созданию новой теории оптимального управления.. Понтрягин и его ученики Болтянский, Галекрелидзе, Мищенко разработали новую теорию.

Основным результатом этой теории является принцип максимума, который определяет необходимые условия оптимальности для широкого круга задач оптимального программного управления известно, что задачи Больца и Лагранжа сводятся к задаче Майера.

Для удобства рассмотрения задачи об оптимальности программном управлении будем полагать объект стационарным автономным, а задачу представим в форме задачи Майера.

Пусть объект управления описывается уравнением

1

Уравнение u ограничено

u u_{предельное} 2

или .

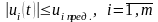Назовем допустимыми уравнениями u_it, те, которые являются кусочно-непрерывными и имеют ограничения вида 2.

Концевые условия

3

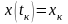4

Функционал качества

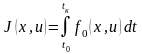5

Требуется перевести объект из xt₀  xt_к, используя только допустимые управления, таким образом, чтобы критерий качества 5) принимал наименьшее значение.

Отметим, в отличие от вариационного исчисления, здесь имеет место ограничение 2), кроме того функции явно не зависят от t стационарные).

Здесь критерий качества выступает в форме Лагранжа

.

Эту задачу можно представить как задачу Майера. Действительно, введем новую координату состояния x₀, которая удовлетворяет дифференциальному уравнению

6)

Дополним левый конец краевых условий 3) равенством

7)

Сформулируем поставленную задачу как задачу Майера: требуется найти допустимое управление, переводящее объект 1), 6)

,

из состояния 3), 7)

в состояние 4)

таким образом, чтобы переменная x₀t) в момент t_к принимала наименьшее значение.

2. Принцип максимума Понтрягина.

Принципом максимума Л.С. Понтрягин назвал теорему о необходимом условии оптимальности.

Пусть объект управления описывается дифференциальными уравнениями:

(8)

где  вектор состояния;

 вектор управления.

Требуется перевести объект из начального состояния при ; 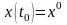в конечное состояние при ; .

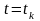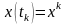Таким образом, краевые условия:

; (9)

и время перевода полагаются заданными. На вектор управления накладывается ограничение

u  V, (10)

где V некоторая ограниченная область.

Требуется определить оптимальное управление u^*t) и траекторию состояния x^*t), которые обеспечивают минимизацию функционала качества

.

Считают, что все функции f_ix,u,t), i=0,1,2,,n непрерывны по переменным x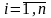_it), ; u_it), , t и непрерывно дифференцируемы по x_it), , t . Управление u^*t) отыскивается в классе кусочно-непрерывных функций из области V. Таким образом, рассматривается задача с закрепленными концами и фиксированным временем.

Для решения задачи вводится дополнительная переменная из условия 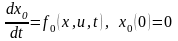, эта переменная определяется функционалом качества x₀=Jx,u) и поэтому в процессе решения задачи должна принимать минимальное значение.

Далее составляется функция Гамильтона Гамильтониан - вспомогательная целевая функция)

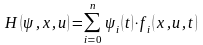, (11)

где функции _it) должны удовлетворять уравнениям:

(12)

Уравнения (11) называют сопряженными. Это вытекает из определенной симметричности записи уравнений:

;

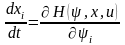
(13)

.

Поскольку все функции f_ix,u,t, i=0,1,2,,n не зависят от переменной x₀, то 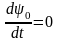и ₀=const.

Формулировка принципа максимума.

Для оптимальности управления u^*=u₁,u₂,,u_m и траектории состояния x^*=x₁,x₂,, x_n необходимо существование такой ненулевой непрерывной функции ^*=₀, ₁,, _n {неопределенных множителей Лагранжа}сопряженных уравнений, что при любом tt₀  t  t_k функция Гамильтона H,x,u переменного uV достигает в точке u=u^*t максимума

при условии ₀  0.