
- •2.Классификация звеньев и их условные изображения на кинематических схемах.
- •3.Классификация кинематических пар и их условные обозначения.
- •5.Число степеней свободы и подвижность механизма.
- •6.Пассивные и избыточные связи, лишние степени свободы.
- •7.Принцип образования плоских механизмов. Понятия структурной группы, исходного механизма. Класс и порядок структурной группы.
- •8.Задачи и методы кинематического анализа.
- •9.План скоростей (ускорений) и его свойства.
- •10.Кинематический анализ структурной группы II класса, 2 порядка, 1 вида методом планов. (написать из лекции)
- •12. Понятие передаточного отношения. Основной закон зацепления. Кинематический расчет зубчатых передач с внешним и внутренним зацеплением колес.
- •14.Кинематический анализ эпициклического механизма.
- •15.Классификация зубчатых механизмов, их строение, свойства. Типы эпициклических механизмов. Схемы эпициклических механизмов.
- •16.Синтез эпициклических механизмов. Условия соосности, соседства, сборки.
- •17.Задачи и методы силового расчета. Условия статической определимости плоской кинематической цепи. Принципы механики.
- •19.Особенности силового расчета исходного механизма (привод через муфту и зубчатый редуктор).
- •20.Задачи динамики и методы их решения. Понятие динамической модели.
- •21.Определение приведенного момента инерции (массы) и приведенного момента сил (силы).
- •22.Уравнения движения машины.
- •23.Режимы движения машины и их краткая характеристика.
- •24.Решение задачи динамического анализа методом Виттенбауэра.
- •25.Коэффициент неравномерности движения машины. Назначение маховика.
- •26.Решение задачи динамического синтеза методом Виттенбауэра.
- •27.Определение уравновешивающей силы (момента сил) методом рычага Жуковского.
- •28.Виды трения, их краткая характеристика. Угол трения.
- •29.Трение во вращательных и поступательных парах. Понятие круга трения.
- •31.Определение кпд при последовательном и параллельном соединении механизмов.
- •32.Основные параметры зубчатого колеса и зубчатого зацепления.
- •33.Эвольвента, ее уравнения и свойства.
- •34.Теоретический исходный и исходный производящий контуры.
- •35.Станочные зацепление. Понятие о подрезании и заострении зуба колеса. Способы устранения дефектов геометрии.
- •36.Критерии качества зубчатой передачи (коэффициенты перекрытия, удельного давления, относительного скольжения).
- •37.Выбор коэффициентов смещения по блокирующим контурам.
- •38.Назначение, строение и классификация кулачковых механизмов.
- •39.Типовые законы движения толкателя и их краткая характеристика.
- •40.Угол давления в кулачковом механизме. Заклинивание кулачкового механизма.
- •49. Расчет сил инерции.
- •50.Виды дисбаланса роторов и способы их уравновешивания.
- •51.Статическое уравновешивание плоских механизмов (на примере кривошипно-коромыслового механизма).
- •52.Полное и неполное статическое уравновешивание кривошипно-ползунного механизма.
- •53.Моментное уравновешивание механизма.
51.Статическое уравновешивание плоских механизмов (на примере кривошипно-коромыслового механизма).
С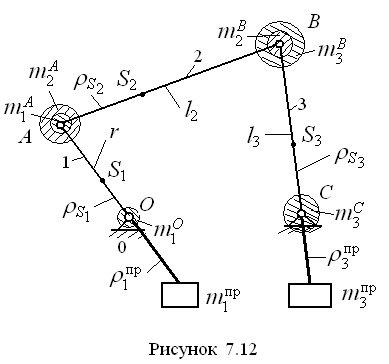 т а т и ч е с к о е у р а в н о в е ш и в а н
и е ч е т ы р ё х ш а р н и р н о- г о м е х
а н и з м а.
Пусть в четырёхшарнирном механизме
OABC
известны массы подвижных звеньев:
– масса кривошипа 1,
– масса шатуна 2 и
– масса коромысла 3. Известны также
длины звеньев:
– длина кривошипа,
т а т и ч е с к о е у р а в н о в е ш и в а н
и е ч е т ы р ё х ш а р н и р н о- г о м е х
а н и з м а.
Пусть в четырёхшарнирном механизме
OABC
известны массы подвижных звеньев:
– масса кривошипа 1,
– масса шатуна 2 и
– масса коромысла 3. Известны также
длины звеньев:
– длина кривошипа,
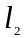 – длина шатуна и
– длина шатуна и
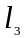 – длина коромысла. Положения центров
масс подвижных звеньев определены их
расстояниями:
– длина коромысла. Положения центров
масс подвижных звеньев определены их
расстояниями:
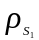 – от точки O
до центра масс
– от точки O
до центра масс
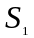 кривошипа,
кривошипа,
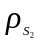 – от точки A
до центра масс
– от точки A
до центра масс
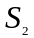 шатуна и, наконец,
шатуна и, наконец,
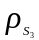 – от точки C
до центра масс
– от точки C
до центра масс
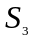 коромысла.
коромысла.
Заменим массы кривошипа, шатуна и коромысла двумя точечными массами каждое и определим величины этих масс.
Согласно
приведённым выше уравнениям получим
следующие выражения для их расчёта:
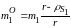 ,
,
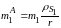 ,
,
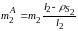 ,
,
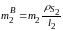 ,
,
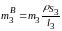 и
и
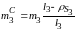 .
.
П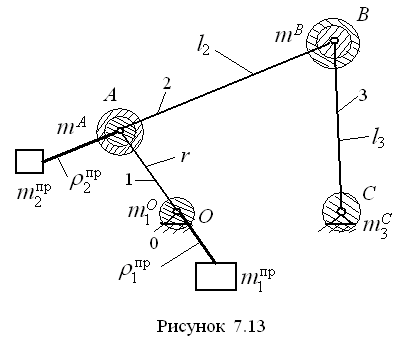 ервый
вариант уравновешивания. Точечные
массы, расположенные в точках O
и C,
неподвижны, поэтому не требуют каких-либо
действий. Точечную массу в точке A
величиной
ервый
вариант уравновешивания. Точечные
массы, расположенные в точках O
и C,
неподвижны, поэтому не требуют каких-либо
действий. Точечную массу в точке A
величиной
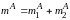 следует уравновесить противовесом
следует уравновесить противовесом
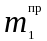 ,
расположив его за точкой O.
При этом общий центр массы
,
расположив его за точкой O.
При этом общий центр массы
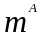 и
должен располагаться в точке O.
Тогда можно записать уравнение
и
должен располагаться в точке O.
Тогда можно записать уравнение
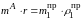 ,
откуда, приняв произвольно радиус
,
откуда, приняв произвольно радиус
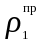 установки противовеса, находим его
массу:
установки противовеса, находим его
массу:
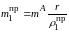 .
Аналогичным образом поступаем с массой
в точке B,
определяемой суммой
.
Аналогичным образом поступаем с массой
в точке B,
определяемой суммой
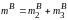 .
Из условия равенства статических
моментов масс
.
Из условия равенства статических
моментов масс
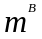 и
и
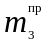 относительно
точки C
имеем
относительно
точки C
имеем
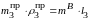 ,
откуда
,
откуда
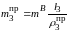 (
(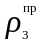 выбирается произвольно).
выбирается произвольно).
Второй
вариант уравновешивания. Разнесём
массы звеньев 1, 2 и 3 в точки O,
A,
B
и C
и обозначим суммарную массу в точке A
как
и суммарную массу в точке B
как
.
Массы, сосредоточенные в точках O
и C,
остаются неподвижными. На продолжении
шатуна влево от точки A
поместим противовес массой
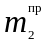 на некотором радиусе
на некотором радиусе
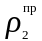 для смещения общего центра масс, связанных
с шатуном, в точку A.
Для этого необходимо выполнить следующее
условие:
для смещения общего центра масс, связанных
с шатуном, в точку A.
Для этого необходимо выполнить следующее
условие:
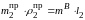 ,
откуда находим
,
откуда находим
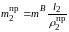 .
Теперь на продолжении кривошипа за
точку O
устанавливается противовес
на радиусе
при условии выполнения следующего
равенства:
.
Теперь на продолжении кривошипа за
точку O
устанавливается противовес
на радиусе
при условии выполнения следующего
равенства:
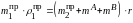 .
Решая это равенство относительно
,
находим
.
Решая это равенство относительно
,
находим
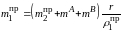 .
.
Радиусы установки противовесов и выбираются произвольно.
Можно установить противовес на продолжении шатуна вправо от точки B. Тогда, вместо противовеса на кривошипе, необходимо установить противовес на коромысле 3 за точкой C.
52.Полное и неполное статическое уравновешивание кривошипно-ползунного механизма.
С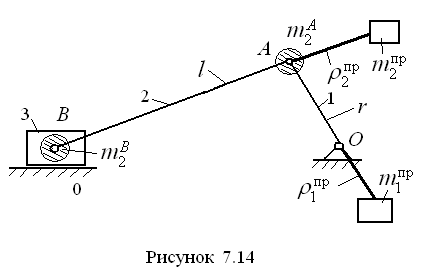 п о с о б ы с т а т и ч е с к о г о у р а в
н о в е ш и в а н и я к р и в о -
ш и п н
о-п о л з у н н о г о м е х а н и з м а.
Способ противовесов аналогичен тому,
который применяется для уравновешивания
четырёхшарнирного механизма во втором
варианте. Сначала уравновешиваются
сосредоточенная масса шатуна
п о с о б ы с т а т и ч е с к о г о у р а в
н о в е ш и в а н и я к р и в о -
ш и п н
о-п о л з у н н о г о м е х а н и з м а.
Способ противовесов аналогичен тому,
который применяется для уравновешивания
четырёхшарнирного механизма во втором
варианте. Сначала уравновешиваются
сосредоточенная масса шатуна
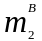 и масса ползуна 3 с помощью противовеса
,
устанавливаемого на продолжении шатуна
2 за точку A.
В результате такой операции общий центр
масс шатуна и ползуна сместится в точку
A.
Величина массы противовеса определится
из уравнения
и масса ползуна 3 с помощью противовеса
,
устанавливаемого на продолжении шатуна
2 за точку A.
В результате такой операции общий центр
масс шатуна и ползуна сместится в точку
A.
Величина массы противовеса определится
из уравнения
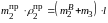 ,
решая которое относительно
,
находим
,
решая которое относительно
,
находим
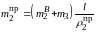 .
.
Теперь
общую массу шатуна, ползуна и противовеса
необходимо уравновесить противовесом
,
устанавливаемым на продолжении кривошипа
за точку O.
Для этого составляется уравнение
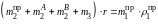 ,
из которого определяем
,
из которого определяем
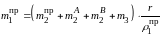 .
Радиусы установки противовесов выбираются
произвольно.
.
Радиусы установки противовесов выбираются
произвольно.
Ч
а с т и ч н о е у р а в н о в е ш и в а н и
е с и л и н е р ц и и п о с т у- п а т е
л ь н о д в и ж у щ и х с я м а с с к р и
в о ш и п н о-п о л з у н н о г о м е х а н и
з м а.
Как указывалось выше, сила инерции
поступательно движущихся масс
кривошипно-ползунного механизма
определяется уравнением
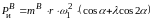 ,
в котором
– масса, сосредоточенная в точке B
и равная
,
в котором
– масса, сосредоточенная в точке B
и равная
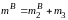 .
Силу инерции
.
Силу инерции
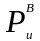 можно представить в виде суммы
можно представить в виде суммы
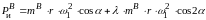 ,
в которой первое слагаемое правой части
называется силой инерции первого порядка
,
в которой первое слагаемое правой части
называется силой инерции первого порядка
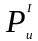 ,
второе слагаемое – силой инерции второго
порядка
,
второе слагаемое – силой инерции второго
порядка
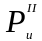 .
Таким образом,
.
Таким образом,
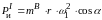 а
а
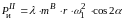 .
Так как
.
Так как
 ,
то
,
то
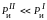 ,
поэтому часто ограничиваются
уравновешиванием силы инерции первого
порядка.
,
поэтому часто ограничиваются
уравновешиванием силы инерции первого
порядка.
П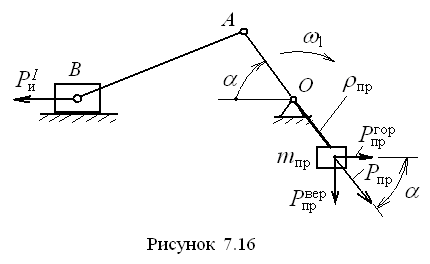 ротивовес
массой
устанавливается на продолжении кривошипа
за точку O
на радиусе
.
Он должен быть подобран таким образом,
чтобы его горизонтальная составляющая
ротивовес
массой
устанавливается на продолжении кривошипа
за точку O
на радиусе
.
Он должен быть подобран таким образом,
чтобы его горизонтальная составляющая
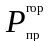 силы инерции
силы инерции
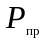 была равна силе инерции первого порядка,
то есть
была равна силе инерции первого порядка,
то есть
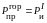 .
.
Как
видно из рис. 7.16, горизонтальная
составляющая силы инерции противовеса
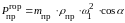 .
Таким образом, имеем равенство
.
Таким образом, имеем равенство
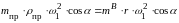 ,
сократив которое на одинаковые множители,
получаем
,
сократив которое на одинаковые множители,
получаем
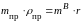 .
Отсюда находим массу противовеса
.
Отсюда находим массу противовеса
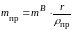 .
.
С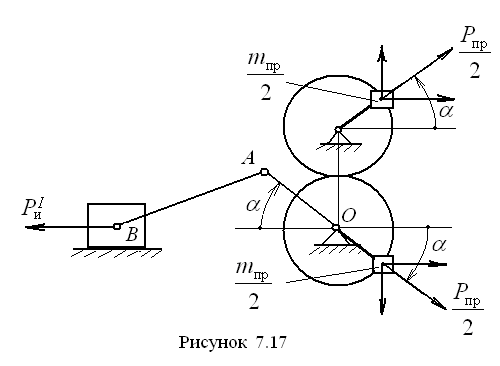 помощью горизонтальной составляющей
силы инерции данного противовеса
уравновешивается сила инерции первого
порядка поступательно движущихся масс
механизма. Однако появляется
неуравновешенная вертикальная
составляющая
помощью горизонтальной составляющей
силы инерции данного противовеса
уравновешивается сила инерции первого
порядка поступательно движущихся масс
механизма. Однако появляется
неуравновешенная вертикальная
составляющая
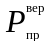 этой силы инерции. Чтобы её уравновесить,
вместо одного противовеса на кривошипе
используют два одинаковых по массе
противовеса, которые устанавливают на
равных радиусах на двух зубчатых колёсах,
образующих внешнее зацепление (рис.
7.17). Одно из колёс жёстко связывают с
кривошипом, и тогда оно вращается с ним
как одно целое. Второе вращается в
противоположную сторону. Массы
противовесов подбираются так, чтобы
сила инерции каждого из них была равна
половине той силы инерции, которая
создаётся одним противовесом в предыдущей
задаче. В любом положении механизма
горизонтальные составляющие этих двух
сил в сумме дадут силу инерции
,
которая уравновешивает силу инерции
этой силы инерции. Чтобы её уравновесить,
вместо одного противовеса на кривошипе
используют два одинаковых по массе
противовеса, которые устанавливают на
равных радиусах на двух зубчатых колёсах,
образующих внешнее зацепление (рис.
7.17). Одно из колёс жёстко связывают с
кривошипом, и тогда оно вращается с ним
как одно целое. Второе вращается в
противоположную сторону. Массы
противовесов подбираются так, чтобы
сила инерции каждого из них была равна
половине той силы инерции, которая
создаётся одним противовесом в предыдущей
задаче. В любом положении механизма
горизонтальные составляющие этих двух
сил в сумме дадут силу инерции
,
которая уравновешивает силу инерции
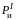 .
Вертикальные же составляющие получаются
равными друг другу и противоположно
направленными, поэтому уравновешивают
друг друга.
.
Вертикальные же составляющие получаются
равными друг другу и противоположно
направленными, поэтому уравновешивают
друг друга.
