49. Расчет сил инерции.

Силы инерции возникают во всех случаях, когда звенья движутся непрямолинейно и/или неравномерно. Рассмотрим три вида движения звеньев.

П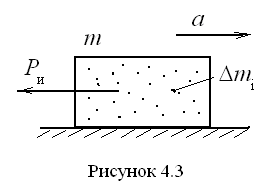 о с т у п а т е л ь н о е д в и ж е н и е з в е н а. Этот вид движения чаще всего относится к ползунам, движущимся относительно прямолинейных направляющих (рис. 4.3). Пусть при этом – масса ползуна, – его ускорение.

Сила инерции элементарной массы звена . Если просуммировать все элементарные силы инерции данного ползуна, то есть найти сумму , то получится главный вектор сил инерции звена, равный . То есть сила инерции звена в его поступательном движении равна массе звена, помноженной на его ускорение. Знак «−» в правой части формулы указывает на противоположность направления силы инерции по отношению к ускорению.

В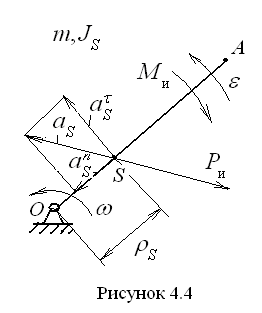 р а щ а т е л ь н о е д в и ж е н и е з в е н а. В этом движении находятся кривошипы, кулисы, коромысла и другие звенья механизмов. Возьмём стержневое звено ОА, вращающееся вокруг неподвижной точки О. Масса звена равна , момент инерции относительно центра масс S равен . Вращение происходит с угловой скоростью и угловым ускорением . Расстояние между центром масс и центром вращения равно .

Вычислим ускорение, с которым движется центр масс S. Его нормальное ускорение равно , тангенциальное ускорение равно . Полное ускорение . Результатом этого ускорения является сила инерции, приложенная в центре масс и направленная противоположно ускорению .

Угловое ускорение звена вызывает появление инерционного момента, направленного по отношению к нему в противоположную сторону .

В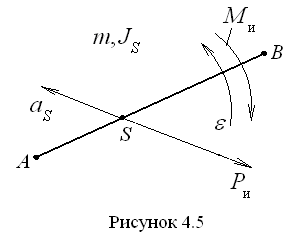 этой формуле момент инерции принимается относительно центра вращения и определяется как .

П л о с к о-п а р а л л е л ь н о е д в и ж е н и е з в е н а. Такое движение совершают чаще всего шатуны механизмов. Масса шатуна равна , момент инерции относительно центра масс равен .

Звено движется, имея угловое ускорение и ускорение центра масс . Аналогично вращательному движению в этом случае также будут действовать оба инерционных фактора: сила инерции , противоположная ускорению центра масс, и момент сил инерции , противоположный угловому ускорению.

Замечание. Как видим, для расчёта сил инерции необходимо знать ускорения, с которыми движутся звенья механизма.

50.Виды дисбаланса роторов и способы их уравновешивания.

Неуравновешенным будем называть такой механизм (или его звено), в котором при движении центр масс механизма (или звена) движется с ускорением.

Неуравновешенность - такое состояние механизма при котором главный вектор или главный момент сил инерции не равны нулю. Различают:

статическую неуравновешенность F_Sм не равно 0 ;

моментную неуравновешенность M_имне равно 0 ;

динамическую неуравновешенность F_Sм¹не равно 0 и M_имне равно 0 .

В зависимости от взаимного расположения оси вращения и главной цетральной оси инерции x-x , различают следующие виды неуравновешенности роторов - статическую, когда эти оси параллельны; - моментную, когда оси пересекаются в центре масс ротора S; - динамическую, когда оси либо пересекаются вне центра масс, либо не пересекаются, а перекрещиваются в пространстве.

2.2. Моментная неуравновешенность.

При моментной неуравновешенности главная центральная ось инерции пересекает ось вращения в центре масс ротора точке S, главный вектор дисбалансов D_с равен нулю, гавный момент дисбалансов М_D не равен нулю т.е. необходимо уравновесить только момент дисбалансов М_D . Для этого достаточно разместить на роторе две одинаковых корректирующих массы m_k на равных расстояниях от оси вращения e_k и от ценра масс S - l_k. Массы выбираются и размещаются так, чтобы момент их дисбалансов M_Dk был по величине равен, а по направлению противоположен моменту дисбалансов ротора М_D:

где D_k = m_k e_k . В этих зависимостях величинами l_k и e_k задаются по условиям удобства размещения противовесов на роторе, а величину m_k рассчитывают. Необходимо отметить, что величины D_k в плоскостях коррекции необязательно должны быть равными, необходимо выполнять только неизменность положения центра масс - он должен оставаться на оси вращения.

В и д ы н е у р а в н о в е ш е н н о с т и. На рис. 7.4. представлен диск с центром масс в точке S. Через центр масс проходят три взаимно перпендикулярные оси I-I, II-II и III-III, называемые центральными главными осями инерции.

О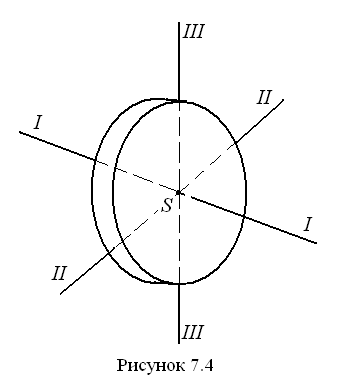 днако оси инерции могут быть одновременно и центральными, и главными. Такие оси и .

Если ось вращения диска совпадает с любой из этих осей инерции, то диск полностью уравновешен. Если ось вращения совпадает с одной из главных осей инерции, но не является центральной (не проходит через центр масс), то имеет место статическая неуравновешенность. Этот вид неуравновешенности легко обнаруживается в статическом состоянии. Если оставить звено свободно вращаться в опорах, то оно будет поворачиваться до тех пор, пока его центр масс не займёт наинизшее положение.

Для приведения в состояние уравновешенности в этом случае требуется установка одного противовеса, который должен переместить ось вращения в центр масс S.

Если ось вращения диска проходит через центр масс (является центральной осью инерции), но не совпадает ни с одной из главных осей, то имеет место динамическая неуравновешенность. В статике её обнаружить невозможно, но если привести диск во вращение, то возникающая пара центробежных сил инерции, создающая неуравновешенный момент, проявит себя в полной мере. В связи с тем, что эта неуравновешенность выявляется в движении (в динамике), она называется динамической. Для динамического уравновешивания требуется установка двух противовесов, создающих момент, противоположный неуравновешенному.

Существует и так называемый общий случай неуравновешенности, объединяющий первые два. Он возникает, если ось вращения звена не является центральной осью инерции и не совпадает ни с одной из его главных осей. Чтобы устранить такую неуравновешенность, требуется три противовеса: один – для статического уравновешивания и два – для динамического.

У с т р а н е н и е с т а т и ч е с к о й н е у р а в н о в е ш е н н о с т и. Пусть конструкция вращающегося звена такова, что оно имеет три неуравновешенные массы , и , вращающиеся вокруг неподвижной точки O на радиусах , и соответственно (рис. 7.5, а). Центробежные силы инерции данных масс определяются формулами: Так как достигнутое уравновешивание действует при любой угловой скорости, то в дальнейшем принимаем . Тогда , и . Определим равнодействующую сил инерции, которую обозначим . Она равна векторной сумме . Построив в масштабе многоугольник сил инерции (рис. 7.5, б), находим . Условие статической уравновешенности звена запишется здесь так: , то есть необходимо установить на звене такой противовес, который бы создавал силу инерции, равную и противоположно направленную равнодействующей сил инерции. Поэтому измеряем вектор и, умножая его на масштаб , находим величину силы инерции противовеса. План сил даёт также ответ на вопрос: где должен располагаться противовес на звене: линия его расположения определяется направлением вектора на плане сил. Перенеся эту линию на звено, выбираем радиус установки , не выходящий за габариты звена, и находим массу противовеса: . На рис. 7.5, а противовес изображён в виде прямоугольника.

У с т р а н е н и е д и н а м и ч е с к о й н е у р а в н о в е ш е н н о с т и. Пусть вращающееся звено имеет форму коленчатого вала поршневой машины (рис. 7.9, а). Центры масс колен вала отмечены буквами S₁ и S₂. Общий центр масс вала S располагается на его геометрической оси, совпадающей с осью вращения. Поэтому вал статически уравновешен. Однако при вращении шатунные шейки испытывают действие центробежных сил инерции и , где и – неуравновешенные массы шатунных шеек вала, причём , и – расстояния между центрами масс шеек и осью вращения вала, здесь также . Эти силы, равные по величине и направленные противоположно друг другу, образуют пару сил с моментом , где – кратчайшее расстояние (плечо) между силами пары.

З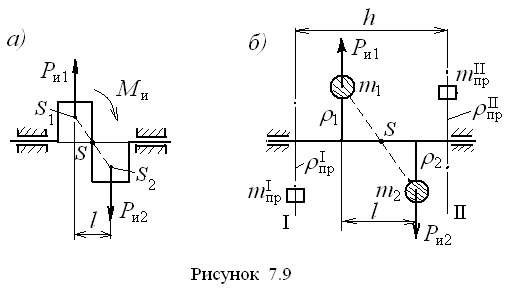 адача уравновешивания в данном случае заключается в создании дополнительного момента за счет противовесов, который должен быть равным и противоположно направленным моменту .

Таким образом, условием уравновешенности вала является равенство . Противовесы располагаются в плоскостях исправления I и II (рис. 7.9, б), как правило, совпадающих с торцами звена (детали). Пусть при этом расстояние между торцевыми поверхностями составляет величину . Тогда можно записать

.

Здесь также имеют место равенства и , поэтому можно применить одно обозначение для масс противовесов – и одно обозначение для радиусов – . Исходя из условия уравновешенности, имеем равенства модулей произведений , откуда находим

Из этой формулы следует, что, имея , необходимо задаться радиусами установки противовесов и рассчитать их массу. Далее следует установить оба противовеса в плоскостях исправления I и II, как показано на рис. 7.9, б.