29.Трение во вращательных и поступательных парах. Понятие круга трения.

Трение в поступательной кинематической паре

Т р е н и е н а н а к л о н н о й п л о с к о с т и. Рассмотрим ползун, находящийся на наклонной плоскости, образующей угол с горизонтом (рис. 5.7, а). Ползун движется вверх по наклонной плоскости со скоростью под действием движущей силы P, направленной под углом к плоскости. На ползун действует также сила Q под углом к вертикали, прижимая ползун к плоскости. И, наконец, на ползун также действует реакция наклонной плоскости, отклонённая от нормали к ней на угол трения .

И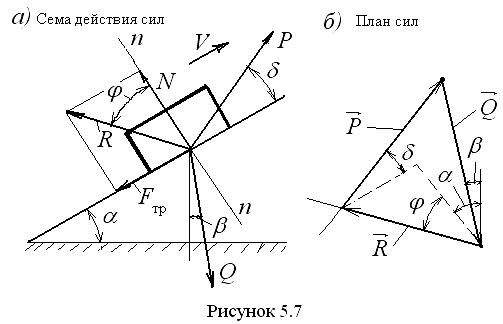 звестными величинами здесь являются сила Q, угол и коэффициент трения f , следовательно, угол . Задача заключается в определении движущей силы P, необходимой для движения ползуна. Она решается с помощью сил, действующих на ползун, согласно уравнению , в котором первый вектор подчёркнут дважды, так как он задан, два другие подчеркнуты одной чертой, так как они известны только по направлению.

Построив треугольник сил (план сил) (рис. 5.7, б), приступаем к его решению. Удобнее всего здесь воспользоваться теоремой синусов, согласно которой в косоугольном треугольнике отношение сторон к синусу противолежащего угла является постоянной величиной (необходимые для решения углы указаны на плане сил)

.

Т р е н и е к л и н ч а т о г о п о л з у н а. Клинчатый ползун часто применяется в виде направляющих металлорежущих станков и другого оборудования, где требуется перемещать вдоль направляющих некоторые устройства, например суппорт станка и др.

Н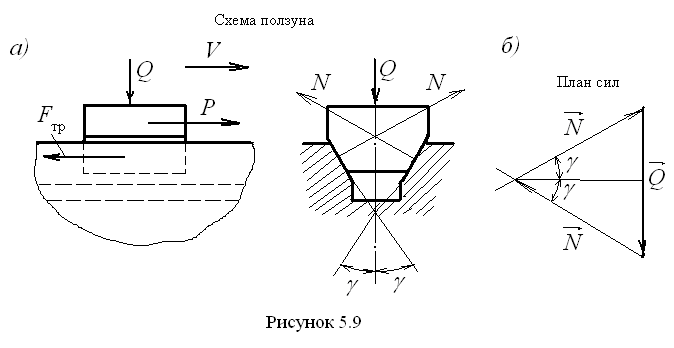 а рис. 5.9, а изображена схема клинчатого ползуна в двух проекциях. На него действует сверху вниз сила Q, которая на боковых наклонных стенках жёлоба вызывает появление нормальных реакций N, а от них затем появляется сила трения . Известными являются сила Q и коэффициент трения . Требуется определить движущую силу P, приводящую в движение ползун в направлении скорости V. Из плана сил ползуна, который построен по уравнению равновесия (рис. 5.9, б), можем определить нормальные составляющие . Здесь мы имеем в виду, что, вследствие симметричности ползуна, модули нормальных реакций справа и слева равны друг другу, и поэтому на плане сил они обозначены одинаково. Итак, . Отсюда следует, что . Так как движущая сила , то . Отношение зависит от условий трения в контакте ползуна с направляющими и от геометрии зоны контакта. Он называется приведённым коэффициентом трения клинчатого ползуна и обозначается , то есть , а движущая сила .

На горизонтальной плоскости угол , поэтому .

Потери мощности на трение в поступательной кинематической паре определяются формулой , причём сила трения вычисляется через реакцию в паре, которую мы научились определять выше в силовом расчёте групп Ассура.

Трение во вращательной кинематической паре

Р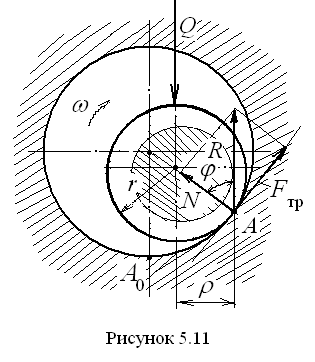 ассмотрим вращательную кинематическую пару в наиболее часто встречающемся случае, когда сопряжение вала с отверстием осуществляется с зазором (рис. 5.11). Вал нагружен поперечной силой , которая является известной величиной. При отсутствии вращения окружность вала касается окружности отверстия в точке на его вертикальном диаметре. Когда вал вращается в направлении , то, в результате действия силы трения , он «взбирается» на стенку вала и в равновесном состоянии устанавливается, касаясь окружности отверстия в точке . При этом реакция стенки отверстия равна и противоположна силе . Нормальная реакция направлена вдоль нормали в точке касания окружностей, то есть вдоль линии, проходящей через точку касания и их центры. Сила трения направлена по касательной к окружностям, проходящей также через точку касания , навстречу окружной скорости вала. Радиус цапфы вала обозначен r (цапфой называется участок вала, который находится внутри отверстия опоры).

Сопротивление вращению вала создаётся моментом трения , равным произведению силы трения на радиус цапфы, то есть . Сила трения, как известно, определяется формулой . Из силового треугольника по теореме Пифагора имеем , или , откуда . Поэтому сила трения , а момент трения . Так как коэффициент трения , то , тогда (например, , , а ). Поэтому можно принять, что . Произведение радиуса цапфы на коэффициент трения является для данных условий постоянной величиной, определяемой только геометрией вала и условиями трения. Эта величина измеряется в линейных единицах, обозначается и называется кругом трения, который описывается этим радиусом при вращении вала (круг трения на рис. 5.11 заштрихован). Так что радиус круга трения . Таким образом, при известном момент трения вычисляется по формуле .

Значение круга трения заключается в том, что полная реакция во вращательной паре проходит по касательной к нему, никогда не пересекая его. При этом её направление таково, что момент реакции относительно центра вала направлен против скорости вращения вала.

30.Понятие КПД механизма, коэффициент потерь. Самоторможение механизма.

Коэффициентом полезного действия (КПД) называется отношение полезной работы, выполняемой в машине, ко всей затраченной. Этот коэффициент является одним из основных критериев качества работы машины или механизма. Он измеряется в процентах или в долях единицы. Если обозначить полезную работу , а всю затраченную, которая является работой движущих сил, – , то отношение первой ко второй, обозначаемое , и будет коэффициентом полезного действия, то есть . Поскольку работа движущих сил тратится на выполнение и работы полезного сопротивления, и работы вредного сопротивления, то можно записать . При определении КПД механизмов из всех видов работ вредного сопротивления учитывается только работа сил трения . Поэтому применительно к механизмам определяется так называемый механический коэффициент полезного действия, определяемый формулой , или . Так как любая работа требует времени, то по этим формулам вычисляется среднее значение за время выполнения работы. Однако во многих случаях целесообразно вычислять мгновенное значение , которое получится, если вместо работ использовать мгновенные мощности. Тогда формула приобретает вид . Поделив числитель на знаменатель, получим , где отношение называется коэффициентом потерь и обозначается , а формула для расчёта представляется в виде .

Самоторможение

Если , то действительного движения механизма произойти не может. Это называется явлением самоторможения. Следовательно, если при теоретических расчетах получим , то механизм в заданном направлении двигаться не может.

Для возможности движения механизма необходимо обеспечить условие .