7. Непрерывность функции Определение 1. Функция f(X) называется непрерывной в точке x0, если .

Более подробно это расшифровывается следующим образом:

1.  .

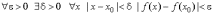2. 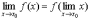 . Другими словами, непрерывная функция характеризуется тем свойством, что можно менять местами знак функции и знак предела.

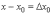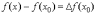3. Обозначим   (приращение аргумента) и    (приращение функции). Тогда непрерывная функция характеризуется тем свойством, что при 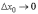   также и 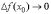  , то есть бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

         Определение 2. Функция f(x) называется непрерывной на множестве Х, если она непрерывна в каждой точке этого множества.

2.2                 Разрывы  функции

Определение. Точки, где функция f(x) не является непрерывной,  называются точками разрыва функции f(x).

Для классификации точек разрыва рассмотрим предел слева 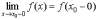  и предел справа 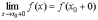  функции f(x). Тогда  имеет место следующая классификация точек разрыва.

1. Устранимый разрыв.

         Он имеет место, когда выполнено условие

.

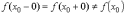         В данном случае достаточно изменить значение функции в точке x₀, чтобы разрыва не стало.

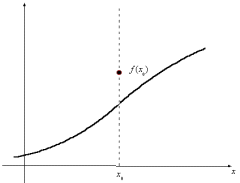
Рис. 2.1 Вид устранимого разрыва

Формулировка

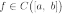Пусть дана непрерывная числовая функция, определённая на отрезке, то есть   и  . Пусть

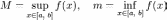
— точные верхняя и нижняя границы множества значений функции   соответственно. Тогда эти значения конечны ( ) и достигаются (существуют 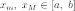 такие, что  ).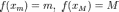

Доказательство

Доказательство для R

Пусть 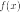  — функция, отвечающая условиям теоремы (на компакте  ),  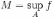. Возьмём последовательность чисел   таких, что 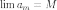  и  . Для каждого 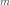 найдётся точка 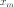 , такая что 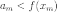 . Имеем дело с компактом, поэтому, согласно теореме Больцано — Вейерштрасса из последовательности   можно выделить сходящуюся последовательность 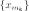 , предел которой лежит в  .

Для любого   справедливо 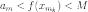 , поэтому, применяя предельный переход, получаем 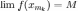  и в силу непрерывности функции существует точка   такая, что 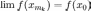  и, следовательно  .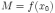

Таким образом функция   ограничена и достигает своей верхней грани при  . Аналогично и для нижней грани.

Замечания

• По определению точки   и   являются точками глобального минимума и максимума соответственно. Таким образом непрерывная на отрезке функция достигает на нём своего минимума имаксимума.

• В предположениях теоремы отрезок нельзя заменить на открытый интервал. Например, функция тангенс

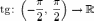
непрерывна в каждой точке области определения, но не ограничена.

• Иногда (в учебных курсах) два утверждения (об ограниченности и достижимости границ) разделяются на две теоремы Вейерштрасса - первую и вторую соответственно^[1].

Обобщения Теорема Вейерштрасса для полунепрерывных функций

• Пусть функция   полунепрерывна сверху. Тогда

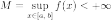 и 

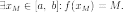
• Пусть функция   полунепрерывна снизу. Тогда

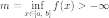 и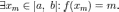 

9. Дифференци́руемая (в точке) фу́нкция — это функция, у которой существует дифференциал (в данной точке). Дифференцируемая на некотором множестве функция — это функция, дифференцируемая в каждой точке данного множества. Дифференцируемость является одним из фундаментальных понятий в математике и имеет значительное число приложений как в самой математике, так и в других естественных науках.

Приращение дифференцируемой в данной точке функции можно представить как линейную функцию приращения аргумента с точностью до величин более высокого порядка малости. Это означает, что для достаточно малых окрестностей данной точки функцию можно заменить линейной (скорость изменения функции можно считать неизменной). Линейная часть приращения функции называется ее дифференциалом (в данной точке).

Необходимым, но не достаточным условием дифференцируемости является непрерывность функции. В случае функции от одной вещественной переменной дифференцируемость равносильна существованию производной. В случае функции нескольких вещественных переменных необходимым (но не достаточным) условием дифференцируемости является существование частных производных по всем переменным. Для дифференцируемости функции нескольких переменных в точке достаточно, чтобы частные производные существовали в некоторой окрестности рассматриваемой точки и были непрерывны в данной точке.^[1]

Для того, чтобы функция f(x) была дифференцируема в точке x0 необходимо и достаточно, чтобы у нее существовала производная в этой точке.  При этом  Δy = f(x0+Δx)-f(x0) = f '(x0)Δx+α(Δx)Δx,  где α(Δx) - бесконечно малая функция, при Δx→0.  для функции одной переменной существование производной в точке является необходимым и достаточным условием дифференцируемости функции в этой точке. Для функции многих переменных дифференцируемость и существование частных производных не являются эквивалентными свойствами функции.Теорема 6 (необходимое условие дифференцируемости). Если функция дифференцируема в точке , то она имеет в точке частные производные по каждой переменной и .  При этом ,, где и – числа из равенства (1). Поэтому условие дифференцируемости (1) можно записать в виде  а полный дифференциал функции – в виде  Обратная теорема не верна, т.е. существование частных производных не является достаточным условием дифференцируемости функции

из дифференцируемости функции следует ее непрерывность.

Рассмотрим более конкретно каждый вопрос. Чтобы ответить на данные вопросы необходимо доказать озвученый факт или привести пример, который опровергает этот факт.

Найдем производную следующей функции 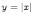  . Хорошо известно, данная функция является непрерывной и, что ее производная будет следующей:

Покажем, что в точке нуль производная не существут. Для этого найдем производную в нуле по определению производной:

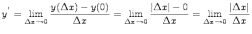
данный предел равен 1, е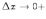сли   и равен (-1), если 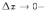  , получаем, что предел не существует, следовательно в нуле производной нет и функция в нуле не дифференцируема. 

Определение. Дифференциалом функции 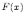  (обозначается через 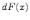  ) называется следующее выражение:

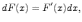
где dx -- дифференциал x при условии, что функция имеет производную.

Предположим, что существует следующее равенство функций:

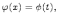
тогда дифференциал от равенства есть

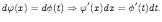
Для решения дифференциальных уравнений используют много разных способов: метод разделения переменных, метод вариации и т.д.

Например, в методе разделения переменных используется определение дифференциала функции т.е.

Также это определение используется во многих других методах. 

Геометрический смысл дифференциала функции

13/ теорема Ролля Если функция y = f(x) 1) непрерывна на отрезке [ab]; 2) дифференцируема во всех внутренних точках этого отрезка; 3) принимает равные значения на концах этого отрезка, то есть f(a) = f(b),  то внутри интервала (ab) существует по крайней мере одна точка х = с, a < c < b, такая, что f′(c) = 0. Доказательство. Пусть M и m – наибольшее и наименьшее значения f(x) на [ab]. Тогда, если m = M, то f(x) = m = M – постоянная функция, и f′(x)=0 для любой точки отрезка [ab]. Если же m<M, то по теореме 16.2 хотя бы одно из значений m или M достигается во внутренней точке с отрезка [ab] (так как на концах отрезка функция принимает равные значения). Тогда по теореме Ферма f′(c) = 0. у у у 0 1 х 0 х -1 0 1 х Рис. 1. Рис. 2. Рис. 3. Замечание 1. В теореме Ролля существенно выполнение всех трех условий. Приведем примеры функций, для каждой из которых не выполняется только одно из условий теоремы, и в результате не существует такой точки, в которой производная функции равна нулю. Действительно, у функции, график которой изображен на рис. 1, f(0)=f(1)=0, но х=1 – точка разрыва, то есть не выполнено первое условие теоремы Ролля. Функция, график которой представлен на рис.2, не дифференцируема при х = 0, а для третьей функции f(-1)≠f(1). Замечание 2. Геометрический смысл теоремы Ролля: на графике рассматриваемой функции найдется по крайней мере одна точка, касательная в которой параллельна оси абсцисс. Теорема Ро́лля утверждает, что если функция, имеющая производную на интервале,принимает в его концах равные значения, то её производная обращается в нуль в некоторой точке внутри интервала.  Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует точка e такая, что в соответствующей точке кривой y = f(x) касательная параллельна оси Ох. Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки. ФОРМУЛА ЛА-ГРАНЖА (конечных приращений) формула конечных приращений Лагранжа,- формула, выражающая приращение функции через значение производной в промежуточной точке. Если функция f непрерывна на отрезке [ а, b]числовой оси и дифференцируема в его внутренних точках, тогда К. п. ф. записывают также в виде Геометрич. смысл К. п. ф.: для хорды графика функции fс концами в точках (а, f(а)), (b, f(b))существует такая точка x, а<x<b, что касательная к графику функции в точке (x, f(x)) параллельна указанной хорде (см. рис.). 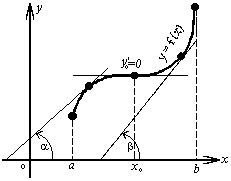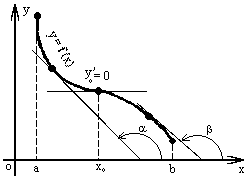Теорема о постоянстве функции, где производная равна 0 производная дифференцируемой функции в точке локального экстремума этой функции равна нулю. Поэтому функция, дифференцируемая на некотором интервале, может иметь на этом интервале локальный экстремум только в тех точках, где её производная равна нулю. Такие точки, т.е. точки, в которых производная функции равна нулю, называются точками возможного экстремума или стационарными точками. Однако в стационарной точке не обязательно достигается локальный экстремум функции. Например, функция  не имеет локального экстремума в стационарной точке x=0. Предположим теперь, что функция дифференцируема всюду на заданном интервале, за исключением конечного числа точек, в которых эта функция не имеет производной. В тех точках, в которых функция имеет отличную от нуля производную, эта функция, , либо возрастает, либо убывает. Поэтому в таких точках локального экстремума быть не может. В остальных точках заданного интервала, т.е. в стационарных точках и в тех точках, где функция не имеет производной, наличие локального экстремума возможно. Так, например, функция y= не имеет производной в точке x = 0, но в этой точке функция имеет локальный минимум (рис. 4). Такие точки, а именно стационарные точки и те точки, в которых функция не имеет производной, называются критическими точками. Для того чтобы выяснить, имеется ли экстремум в критической точке, требуется дополнительное исследование. Рассмотрим достаточное условие достижения функцией локального экстремума в критической точке.

Функция, которая является либо невозрастающей на X, либо неубывающей на X, называется монотонной на X.

Функция f(x) называется возрастающей в интервале (a,b), если при возрастании аргумента x в этом интервале соответствующие значения функции f(x) также возрастают, т.е. если

f(x₂) > f(x₁) при x₂ > x₁.

Рис.1 (а)

Рис.1 (б)

  Из этого определения следует, что у возрастающей в интервале (a,b) функции f(x) в любой точке этого интервала приращения x и y имеют одинаковые знаки.

Функция f (x) называется убывающей в интервале ( a, b ) если при возрастании аргумента x в этом интервале соответствующие значения функции f (x) убывают, т.е. если

f(x₂) < f(x₁) при x₂ > x₁.

  Из этого определения следует, что у убывающей в интервале ( a, b ) функции f (x) в любой точке этого интервала приращения x и y имеют разные знаки.

Необходимые и достаточные условия монотонности

(Критерий монотонности функции, имеющей производную на интервале) Пусть функция   непрерывна на   и имеет в каждой точке  производную   Тогда

 не убывает на   тогда и только тогда, когда 

 не возрастает на   тогда и только тогда, когда 

(Достаточное условие строгой монотонности функции, имеющей производную на интервале) Пусть функция   непрерывна на   и имеет в каждой точке   производную   Тогда

если   то   строго возрастает на 

если   то   строго убывает на 

Обратное, вообще говоря, неверно. Производная строго монотонной функции может обращаться в ноль. Однако, множество точек, где производная не равна нулю, должно быть плотнона интервале   Точнее имеет место

(Критерий строгой монотонности функции, имеющей производную на

интервале) Пусть   и всюду на интервале определена производная   Тогда  строго возрастает на интервале   тогда и только тогда, когда выполнены следующие два условия:

Аналогично,   строго убывает на интервале   тогда и только тогда, когда выполнены следующие два условия:

Достаточные признаки возрастания и убывания функции.

если производная функции y = f(x) положительна для любого x из интервала X, то функция возрастает на X;

если производная функции y = f(x) отрицательна для любого x из интервала X, то функция убывает на X. Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:

найти область определения функции;

найти производную функции;

решить неравенства   и   на области определения;

к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.

Теорема 1. Первое достаточное условие локального экстремума.     Пусть точка α является критической точкой дифференцируемой в некоторой окрестности рассматриваемой точки функции f(x). Тогда, если слева от точки α производная f ' (x) положительна, справа -- отрицательна,  то критическая точка α является точкой локального максимума.  Если же слева от критической точки α производная f ' (x) отрицательна, а справа положительна, то α есть точка локального минимума.

Теорема 2. Второе достаточное условие локального экстремума.   Пусть α критическая точка  дифференцируемой в некоторой окрестности точки α функции f(x) и пусть в этой  точке у рассматриваемой функции существует вторая производная f '' (α). Тогда, если вторая производная f '' (α)<0, то критическая точка αявляется точкой локального максимума, а если f '' (α)>0, то α есть точка локального минимума.

Помимо точек, в которых существует и равна нулю первая производная  функции, локальные экстремумы могут находиться в точках, где первая производная не существует. Поскольку такие случаи не редкость, рассмотрим их подробнее. Оказывается, Теорема 4.1  в  измененной форме может оказаться полезной при рассмотрении таких точек.  

Теорема3. в окрестности. Пусть функция f(x) непрерывна в точке α и у нее всюду в некоторой окрестности    этой  точки, но за исключением самой точки α, существует первая производная. Тогда, если в   производная f ' (x) положительна (отрицательна) слева от α и отрицательна  (положительна) справа от α, то в точке αфункция f(x) имеет локальный максимум (минимум).

Теорема 2 не позволяет сделать определенного заключения о характере критической точки α функции f(x), если в этой точке вторая производная  обращается в нуль: f '' (α)=0. Если в точке α у рассматриваемой функции существуют производные более высокого порядка, то их можно привлечь для разрешения вопроса о наличии или отсутствии локального экстремума в критической точке.

Теорема 4. Не деф. в данной точки Пусть в критической точке α у функции f(x) существуют производные  до порядка n ≥ 3, причем выполняются соотношения                              f ' (α) = 0,         f '' (α) = 0,   ...            (α) ≠ 0.  Тогда, если n- четное число, то критическая точка α является точкой локального экстремума. Точнее, при  (α)<0 в точке α локальный максимум, а при  (α)>0 точка α есть точка локального минимума.  Если же n нечетное число, то в точке α нет локального экстремума.

 График функции y=f(x) называется выпуклым (вогнутым) на интервале (a,b), если касательная к графику, проведенная в любой точке этого интервала, расположена над (под) графиком функции.

                  Выпуклый график,                 Вогнутый график,

                         <0.                                >0.

 Если вторая производная дважды дифференцируемой функции на некотором интервале отрицательна (положительна), то график функции на данном интервале выпуклый (вогнутый).

Верна и обратная теорема.

Точки перегиба

Точки, в которой график функции меняет направление выпуклости, называют точками перегиба  графика функции.

с

                                                                          Асимптоты

Во многих случаях построение графика функции облегчается, если предварительно построить асимптоты кривой.Прямая называется асимптотой кривой, если расстояние от переменной точки М кривой до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-либо ветви кривой.Различают три вида асимптот: вертикальные, горизонтальные и наклонные.

Вертикальные асимптоты. Прямая x = a является вертикальной асимптотой графика функции f(x), если выполняется хотя бы одно из условий:

или

(при этом функция f(x) может быть вообще не определена соответственно при

и

).

Замечание. Символом

о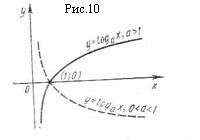 бозначается стремление x к a справа, причём x остаётся больше a, символом

стремление x к a слева, причём x остаётся меньше a.

Из сказанного следует, что вертикальные асимптоты кривой нужно искать в точках разрыва и на границах области определения. График функции, непрерывной на всей числовой прямой, вертикальных асимптот не имеет.

Пример 19. График функции y = ln x имеет вертикальную асимптоту x = 0 на границе области определения, так как

(рис. 10).

Горизонтальные асимптоты. Если

то y = b – горизонтальная асимптота кривой y = f(x) (правая при  , левая при  и двусторонняя, если пределы при  равны).

Пример 20. График функции

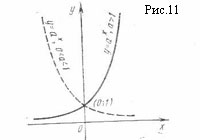
при a > 1 имеет левую горизонтальную асимпототу y = 0, так как

Правой горизонтальной асимптоты у кривой нет, поскольку

(рис. 11).

Наклонные асимптоты. Существование наклонной асимптоты определяется следующей теоремой.

Теорема. Для того, чтобы кривая y = f(x) имела асимптоту y = kx + b, необходимо и достаточно, чтобы существовали конечные пределы

          (33)

или

      (34)

В первом случае получается правая наклонная асимптота, во втором – левая. Правая наклонная асимптота изображена на рис. 13.

П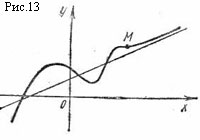 ри совпадении пределов (33) и (34) прямая y = kx + b является двусторонней асимптотой кривой.

Если хотя бы один из пределов, определяющих асимптоту y = kx + b, не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).

Нетрудно видеть, что горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0.

Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.

 Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет.

Наклонная асимптота так же, как и горизонтальная, может быть односторонней.

Исследование функций и построение графиков

С помощью дифференциального исчисления можно установить характерные особенности изменения функций: возрастание и убывание, максимумы и минимумы, направление выпуклости и вогнутости графика, наличие асимптот. Характерные точки – точки разрыва, экстремума, перегиба, пересечения с осями координат – служат опорными точками при исследовании функций и построения их графиков.

Обычно используют следующую схему исследования функции.

1. Находят область определения, интервалы непрерывности и точки разрыва функции.

2. Исследуют функцию на чётность или нечётность (осевая или центральная симметрия графика.

Функция y = f(x) называется чётной, если

График чётной функции симметричен относительно оси Oy, так как, по определению, вместе с любой своей точкой (x; y) он содержит и точку (-x; y).

Функция y = f(x) называется нечётной, если

График нечётной функции симметричен относительно начала координат, так как, по определению, вместе с любой своей точкой (x; y) он содержит и точку (-x; -y).

3. Находят асимптоты (вертикальные, горизонтальные или наклонные).

4. Находят интервалы монотонности функции, точки её экстремума.

Ф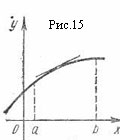 ункции, убывающие или возрастающие на некотором числовом промежутке, называются монотонными функциями.

Функция называется возрастающей на интервале ]a, b[, принадлежащем области определения функции, если бОльшим значениям независимой переменной из этого интервала соответствуют бОльшие значения функции, т.е. если

Функция называется убывающей на интервале ]a, b[, если бОльшим значениям независимой переменной из этого интервала соответствуют меньшие значения функции, т.е. если

5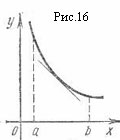 . Находят интервалы выпуклости и вогнутости кривой, точки её перегиба.

График дифференцируемой функции называется выпуклым в интервале ]a, b[, если в этом интервале он расположен ниже любой своей касательной (рис. 15).

График дифференцируемой функции называется вогнутым в этом интервале он расположен выше любой своей касательной  (рис. 16).

Теорема (достаточный признак вогнутости или выпуклости графика). Если для функции f(x) во всех точках интервала ]a, b[

то кривая y = f(x) вогнута в этом интервале; если же

во всех точках интервала ]a, b[, то кривая выпукла в этом интервале.

Т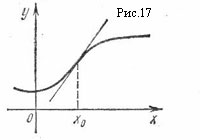 очка графика непрерывной функции, в которой изменяется выпуклость на вогнутость или наоборот, называется точкой перегиба.

Из определения следует, что с одной стороны от точки перегиба кривая расположена под касательной, с другой стороны – над ней, или наоборот. Поэтому точку перегиба на графике принято показывать отрезком касательной, которая в этой точке пересекает кривую (рис. 17).

Теорема (достаточный признак существования точки перегиба). Если в точке  функция f(x) имеет первую производную  , а вторая производная  в этой точке равна нулю или не существует, и кроме того, при переходе через  меняет знак, то

является точкой перегиба графика функции y = f(x).

6. Находят точки пересечения кривой с осями координат, если они существуют.

7. Составляют сводную таблицу исследования.

8. Строят график функции.    

                                       а         y=f(x)                                    

точкой перегиба графика функции y = f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки  , в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости. точкой перегиба графика функции, если в этой точке существует касательная и график функции меняет направление выпуклости, проходя через нее.

Точка a является точкой перегиба, а точка c нет, так как в этой точке функция не дифференцируема.

(необходимый признак точки перегиба). Если точка х₀ является точкой перегиба графика дважды дифференцируемой функции, то в этой точке вторая производная равна нулю:  =0.

 Точки, в которых вторая производная равна нулю или не существует, называются критическими точками второй производной. Если функция имеет точки перегиба, то они могут быть только в критических точка

 (достаточный признак точки перегиба). Если вторая производная дважды дифференцируемой функции в некоторой точке равна нулю и при переходе через нее вторая производная меняет знак, то данная точка является точкой перегиба.