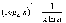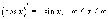10. Дифференцирование сложной функции

позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке  , а функция g имеет производную в точке  , то сложная функция h(x) = g(f(x)) также имеет производную в точке 

усть даны функции, определённые в окрестностях на числовой прямой,   где   и   Пусть также эти функции дифференцируемы:   Тогда их композиция также дифференцируема:   и её производная имеет вид:

Замечание Инвариантность формы первого дифференциала

Дифференциал функции   в точке   имеет вид:

где   — дифференциал тождественного отображения  :

Пусть теперь   Тогда  , и согласно цепному правилу:

Таким образом, форма первого дифференциала остаётся одной и той же вне зависимости от того, является ли переменная функцией или нет.

Пример

Пусть   Тогда функция   может быть записана в виде композиции   где

Дифференцируя эти функции отдельно:

получаем

Производная суммы (разности) функций

Производная алгебраической суммы функций выражается следующей теоремой.

Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:

Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,

Производная произведения функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и

Производная произведения двух функций не равана произведению производных этих функций.

Производная частного функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле

12. Возрастание и убывание функции. Точки максимума и минимума функции

Рассмотрим приложение производной функции к исследованию поведения функции. По первой производной функции можно определить промежутки возрастания и убывания функции, а также определить точки экстремума функции (максимум и минимум).

Определение. Функция   называется возрастающей в точке   , если в некоторой   -окрестности этой точки справедливо

для любого   .

Определение. Функция   называется возрастающей на отрезке   , если для любых двух точек   справедливо неравенство

когда   .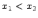

Определение. Функция   называется убывающей в точке   , если в некоторой   -окрестности этой точки справедливо неравенство

для любого   .

Определение. Функция   называется убывающей на отрезке   , если для любых двух точек   справедливо неравенство

когда   .

Определение. Функция   имеет в точке   максимум, если значение   является наибольшим в некоторой двустороней окрестности точки   .

Определение. Функция   имеет в точке   минимум, если значение   является наименьшим в некоторой двусторонней окрестности точки   .

Определение. Функция   имеет в точке   экстремум, если точка   является точкоймаксимума или минимума.

Признаки (достаточные) возрастания и убывания функции   :

Если   на интервале   , то функция   возрастает на этом интервале;

Если   на интервале   , то функция   убывает на этом интервале.

Необходимое условие экстремума функции.

Функция   может иметь экстремум только в точках, где 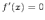  или производная не существует. Точка, где   или производная не существует называется критической точкой.

Заметим, что если в точке   выполняется, что   , то это означает, что касательная в данной точке параллельная оси   . Если производная в точке   не существует, то это значит либо касательная вертикальная, либо ее нет в данной точке.

Достаточные условие экстремума функции.

Если функция   непрерывна в точке   и имеет в некоторой окрестности точки   , кроме, быть может самой точки   , конечную производную и если при переходе   через точку  :

 меняет знак с '+' на '-', то точка   -- точка максимума;

 меняет знак с '-' на '+', то точка   -- точка минимума;

 не меняет знак, то точка   не является точкой экстремума.

Локальный минимум — Экстремум (лат. extremum крайний) в математике максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум точка экстремума

11.

Производная показательной и логарифмической функции

Предполагается, что основание a показательной и логарифмической функции больше нуля и не равно единице: a > 0, a ≠ 1. Производная показательной функции y = ax с основанием a определяется формулой где ln a - натуральный логарифм a, т.е. логарифм a по основанию е, приблизительно равному 2,718281828... (2.7, затем два раза год рождения Л.Н.Толстого). Знаменитое трансцендентное число е можно вычислить с любой степенью точности с помощью различных компьютерных алгоритмов.  Если a = е, то получаем красивый результат в виде Производная логарифмической функции y = loga x определяется выражением Для натурального логарифма y = ln x производная равна

Производные тригонометрических функций

Производные шести тригонометрических функций и, соответственно, шести обратных тригонометрических функций определяются следующими формулами (рядом указана область определения каждой функции): В приведенных ниже примерах мы предполагаем, что читатель (или если кто предпочитает - "пользователь") знаком с основными тригонометрическими формулами.