Элементы линейной алгебры 1 Билет Определитель-многочлен от элементарной квадратной матрицы

Для матрицы 2x2:

Для матрицы 3x3:

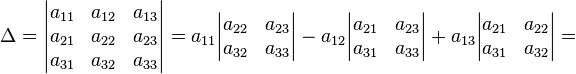
Свойства:  При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.  Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.  Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.  Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).  Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.  Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.  Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.  Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.  Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей.

2 Билет Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Операции над матрицами: 1) Умножение матрицы на число Свойства умножения матриц на число: 1. 1A = A; 2. (λβ)A = λ(βA) 3. (λ+β)A = λA + βA 4. λ(A+B) = λA + λB

2)Сложение матриц Свойства сложения матриц:

1.коммутативность: A+B = B+A;

2.ассоциативность: (A+B)+C =A+(B+C);

3.сложение с нулевой матрицей: A + Θ = A;

4.существование противоположной матрицы: A + (-A) = Θ; 3)Умножение матриц Свойства умножения матриц: 1.ассоциативность (AB)C = A(BC); 2.некоммутативность (в общем случае): AB BA; 3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA; 4.дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC; 5.ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB); 3 Билет Обратная матрица— такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Таким образом, правило Крамера позволяет найти единственное решение системы (2.3) или сделать вывод о существовании бесконечного числа решений либо об их отсутствии:

1. Если система (2.3) имеет единственное решение, определяемое по формулам: .

2)Если = =0, система имеет бесконечно много решений.

3)Если =0, а хотя бы один из система не имеет решений. 4 Билет Ранг матрицы – это порядок ее наибольшего ненулевого минора. . Базисным минором матрицы называется любой ее ненулевой минор, порядок которого равен рангу матрицы Теорема о ранге-Строки и столбцы матрицы, элементы которых входят в базисный минор, линейно независимы. Любая строка (столбец) матрицы является линейной комбинацией этих строк (столбцов). Теорема 4.2 (теорема Кронекера-Капелли). Система (2.2) совместна тогда и только тогда, если ранг матрицы системы равен рангу расширенной матрицы. Решение неоднородной системы уравнений-сумма общего решения соответствующего однородной системы и частного решения системы 5 билет Пример

Покажем, как методом Гаусса можно решить следующую систему:

Обнулим коэффициенты при во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на и , соответственно:

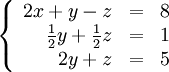
Теперь обнулим коэффициент при в третьей строке, вычтя из неё вторую строку, умноженную на :

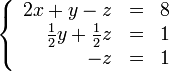В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.

На втором этапе разрешим полученные уравнения в обратном порядке. Имеем: из третьего;

из второго, подставив полученное

из первого, подставив полученные и .Аналитическая геомтрия.

1. 1 Вектором называется направленный отрезок.

Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Вектор называется нулевым, если его начальная и конечная точки совпадают. Нулевой вектор не имеет определенного направления.

Два вектора называются равными, если они коллинеарны, имеют одинаковую длину (модуль) и одинаковое направление.

1.2 Суммой a + b векторов a и b называется вектор, идущий из начала вектора а в конец вектора b, если начало вектора b совпадает с концом вектора а.

Свойства сложения: a + b = b + a.

(a+b)+c=a+(b+c).

Для любого вектора a существует нулевой вектор О такой, что a+О=а.

Для каждого вектора a существует противоположный ему вектор a^/ такой, что а+а^/=О.

Разностью а – b векторов а и b называется такой вектор с, который в сумме с вектором b дает вектор а.

Произведением ka вектора а на число k называется вектор b, коллинеарный вектору а, имеющий модуль, равный |k||a|, и направление, совпадающее с направлением а при k>0 и противоположное а при k<0.

Свойства умножения вектора на число:

k(a + b) = ka + kb.

(k + m)a = ka + ma.

k(ma) = (km)a.

Если ненулевые векторы а и b коллинеарны, то существует такое число k, что b = ka.

1.3 Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними:

ab = |a||b| cosφ . Обозначения скалярного произведения: ab, (ab), a·b

Свойства скалярного произведения:

1. ab = |a| пр_аb.

2. ab = 0 a b. 3. ab = ba .

4. (ka)b = k(ab). 5. (a + b)c = ac + bc .

6. a² = aa = |a|² , где а² называется скалярным квадратом вектора а.

7. Если векторы а и b определены своими декартовыми координатами

a = {X₁, Y₁, Z₁}, b = {X₂, Y₂, Z₂}, (5.5)

то ab = X₁X₂ + Y₁Y₂ + Z₁Z₂ .

8. cosφ = .

2.1 Вектор с называется векторным произведением векторов а и b, если:

1. |c| = |a||b|sinφ, где φ – угол между а и b.

2. c a, c b.

3. Тройка векторов abc является правой.

Обозначения векторного произведения: c = [ab], c = a b.

Свойства векторного произведения.

[ba] = - [ab].

[ab] = 0 a ║ b. sinφ = 0

Модуль векторного произведения |[ab]| равняется площади S параллелограмма, построенного на приведенных к общему началу векторах а и b.

3.1 . Смешанным произведением векторов а, b и с называется результат скалярного умножения векторного произведения [ab] на вектор с.

Обозначение: abc = [ab]c.

3.2 Свойства смешанного произведения.

Если a = {X_a, Y_a, Z_a}, b = {X_b, Y_b, Z_b}, c = {X_c, Y_c, Z_c}, то

abc = .

Если a,b,c не компланарны, [ab]c = |[ab]||c| = S·|c|cosφ, где φ – угол между с и [ab]. Тогда |c|cosφ – высота рассматриваемого параллелепипеда. Таким образом, [ab]c = V, где выбор знака зависит от величины угла между с и [ab].

1. Смешанное произведение [ab]c равно объему параллелепипеда, построенного на приведенных к общему началу векторах a,b,c, если они образуют правую тройку, или числу, противоположному этому объему, если abc – левая тройка. Если a,b и с компланарны, то [ab]c = 0.

4. общее уравнение прямой: Ах + Ву + С = 0.

Каноническое уравнение прямой:

, Вектор q (l,m )при этом называется направляющим вектором прямой.

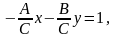
- уравнение прямой в отрезках. где и равны величинам отрезков, отсекаемых прямой на осях Ох и Оу.

у = kx + b - уравнение прямой с угловым коэффициентом. угловой коэффициент k – тангенс угла, образованного прямой и осью Ох

- нормальное уранвение прямой, где   - угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.

Расстояние от точки до прямой определяется так-

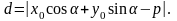
Если прямые L₁ и L₂ заданы общими уравнениями

А₁х + В₁у + С₁ = 0 и А₂х + В₂у + С₂ = 0,

то угол между ними равен углу между их нормалями, то есть между векторами {A₁,B₁} и {A₂,B₂}. Следовательно,

- условие параллельности, - условие перпендикулярности.

Если прямые заданы каноническими уравнениями (7.5), по аналогии с пунктом 1 получим:

,

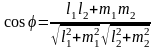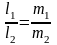- условие параллельности, - условие перпендикулярности.

Здесь и - направляющие векторы прямых.

Пусть прямые L₁ и L₂ заданы уравнениями с угловыми коэффициентами (7.8)

у = k₁x +b₁ и y = k₂x + b₂, где , а α₁ и α₂ – углы наклона прямых к оси Ох, то для угла φ между прямыми справедливо равенство: φ = α₂ - α₁. Тогда

.

5. Ax + By + Cz + D = 0, где

D = -Ax₀ - By₀ - Cz₀. Это линейное уравнение относительно трех переменных называют общим уравнением плоскости.

называемому уравнением плоскости в отрезках. Способ преобразования показан в лекции 7. Параметры а, b и с равны величинам отрезков, отсекаемых плоскостью на координатных осях.

Нормальным уравнением плоскости называется ее уравнение, написанное в виде

, где  ,  ,   - направляющие косинусы нормали плоскоти, p - расстояние от начала координат до плоскости.

При этом расстояние от любой точки А пространства до данной плоскости определяется по формуле:

Условие параллельности плоскостей заключается в параллельности нормалей

а условие перпендикулярности плоскостей – в перпендикулярности нормалей или равенстве нулю их скалярного произведения:

A₁A₂ + B₁B₂ + C₁C₂ = 0.

6. Первая возможность составить уравнения прямой в пространстве – представить эту прямую как пересечение двух непараллельных плоскостей, заданных уравнениями

A₁x+B₁y+C₁z+D₁=0 и A₂x+B₂y+C₂z+D₂=0, где коэффициенты A₁,B₁,C₁ и A₂,B₂,C₂ не пропорциональны:

A₁x+B₁y+C₁z+D₁=0 ₂x+B₂y+C₂z+D₂=0.

называемые каноническими уравнениями прямой в пространстве.

Если же принять каждую из равных дробей в уравнениях (8.11) за некоторый параметр t, можно получить так называемые параметрические уравнения прямой:

Угол между прямыми в пространстве равен углу между их направляющими векторами. Поэтому, если две прямые заданы каноническими уравнениями вида

и косинус угла между ними можно найти по формуле:

.

Условия параллельности и перпендикулярности прямых тоже сводятся к соответствующим условиям для их направляющих векторов:

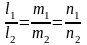- условие параллельности прямых,

- условие перпендикулярности прямых.

Угол φ между прямой, заданной каноническими уравнениями

и плоскостью, определяемой общим уравнением

Ax + By + Cz + D = 0,

можно рассматривать как дополнительный к углу ψ между направляющим вектором прямой и нормалью к плоскости. Тогда

Условием параллельности прямой и плоскости является при этом условие перпендикулярности векторов n и а:

Al + Bm + Cn = 0,

а условием перпендикулярности прямой и плоскости – условие параллельности этих векторов: A/l = B/m = C/n.

1.Билет

Числовой последовательностью называется бесконечное множество чисел

  (1)

следующих одно за другим в определенном порядке и построенных по определенному закону, с помощью которого задается как функция целочисленного аргумента, 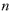т.е. .

Число А называется пределом последовательности (1), если для любого  существует число , такое, что при выполняется неравенство . Если число А есть предел последовательности (1), то пишут

Последовательность называется сходящейся, если существует такое число a, что последовательность является бесконечно малой. При этом число a называется пределом последовательности .

Бесконечно малая последовательность

Определение. Последовательность называется бесконечные малой, если для любого положительного числа ε можно указать номер N такой, что при 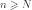все элементы этой последовательности удовлетворяют неравенству .

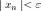Свойства бесконечно малых последовательностей

1. Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.

2. Разница двух бесконечно малых последовательностей есть бесконечно малая последовательность.

3. Бесконечно малая последовательность ограничена.

4. Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность.

5. Если все элементы бесконечно малой последовательности, начиная с некоторого номера, равны одному и тому же числу, то это число - ноль.

6 (а). Если - бесконечно большая последовательность, то начиная с некоторого номера определена последовательность , причём она является бесконечно малой.

6 (б). Если - бесконечно малая последовательность, то начиная с некоторого номера определена последовательность , причём она является бесконечно большой.

Бесконечно большая последовательность

Определение. Последовательность называется бесконечно большой, если для любого положительного числа A можно указать номер N такой, что при все элементы этой последовательности удовлетворяют неравенству .

Теоремы о пределах:

1. Последовательность, имеющая предел,  ограничена.

2. Последовательность может иметь только один предел.

3. Любая неубывающая (невозрастающая) и  ограниченная сверху (снизу) последовательность имеет предел.

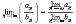
4. Предел постоянной равен этой  постоянной: 5. Предел суммы равен сумме пределов: 6. Постоянный множитель можно  выносить за знак предела: 7. Предел произведения равен произведению пределов: . 8. Предел частного равен частному  пределов, если предел делителя отличен от нуля:   9. Если  и обе последовательности и имеют один и тот же предел а, то В теоремах 5—8 предполагается, что все  пределы в правой части равенств существуют!!! 

2.Билет

Предел функции в точке.

Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.

Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности такой, что сходящейся к числу a, соответствующая последовательность значений функции 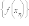сходится к числу A.

Функция α (x) называется бесконечно малой при , если

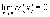
Операции над бесконечно малыми функциями.  

1. Если функции   и   являются  бесконечно малыми, то функция   также есть бесконечно малая. Это свойство распространяется на случай  алгебраической суммы любого конечного числа бесконечно малых.  

2. Произведение ограниченной при    функции на бесконечно малую есть функция бесконечно малая.  

3. Произведение постоянной на бесконечно малую есть бесконечно малая.  

4. Произведение двух бесконечно малых есть бесконечно малая. Это свойство распространяется на любое  конечное число бесконечно малых.  

Свойства пределов функции

Свойства пределов функции:

Теорема 1. Предел суммы равен сумме пределов, если они существуют: 

Теорема 2. Предел произведения равен произведению пределов, если они существуют: 

Теорема 3. Предел частного равен частному пределов:  . При условии: все пределы существуют и  .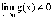

Принцип двустороннего ограничения:

Если функция   такая, что  для всех   в некоторой окрестности точки  , причем функции   и   имеют одинаковый предел при  , то существует предел функции   при  , равный этому же значению, то есть