13. Охлаждение (нагревание) тел конечных размеров.

Рассмотрим охлаждение параллелепипеда в среде с постоянной температурой и постоянным  на всех его гранях. В начальный момент времени (τ=0) все точки параллелепипеда имеют одинаковую температуру t₀. Параллелепипед с размерами является однородным и изотропным. Требуется найти распределение температуры в параллелепипеде для любого момента времени, а также среднюю температуру, необходимую для определения количества подведенного (отведенного) тепла. Начало координат в центре параллелепипеда. Дифференциальное уравнение запишется

Начальные условия (τ=0),

Задача симметрична относительно центра параллелепипеда.

Если ввести обозначение , то граничные условия запишутся:

а)для поверхности при (τ>0)

б) в центре параллелепипеда при (τ=0)

Параллелепипеды, цилиндры конечных размеров и прямоугольные стержни можно рассматривать как тела, образованные пересечением взаимно перпендикулярны соответствующих трех пластин, цилиндра и пластины, и 2-х пластин неограниченных размеров, но конечной толщины. Для параллелепипеда решение можно представить как произведение безразмерных температур для 3-х безграничных пластин:

Ө= Өх Өу Өz, где

; ; ;

тогда

Уравнение для безразмерной температуры параллелепипеда еще можно представить:

или

Средняя безразмерная температура

или

Охлаждение длинного прямоугольного стержня

Охлаждение цилиндра конечной длины

Ø цилиндра , l=2 δ_х

Конечный цилиндр результат пересечения безграничного цилиндра диаметрами пластины толщиной 2 δ_х

или

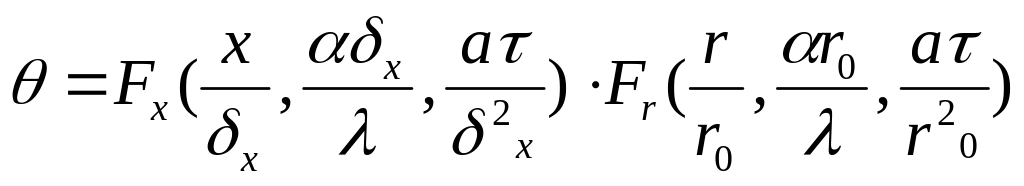
В качестве определения линейных размеров в уравнении  берется половина высоты цилиндра l/2 и радиус r₀

Например температура в 2-х точках цилиндра будет:

1) на поверхности цилиндра в середине

= и х=0, тогда R=1; Х=0

2) в центре основания цилиндра (R=0 и Х =1)

Средняя безразмерная температура в цилиндре для любого момента времени:

или

14. Метод конечных разностей.

Сущность метода заключается в том, что в дифференциальном уравнении

производные заменяются конечными разностями и температурное поле представлено в виде ломанной кривой.

Рассмотрим охлаждение однородной плоской стенки в среде с постоянной температурой и .

В момент времени τ=0 t =f (x) при этом уравнение теплопроводности будет иметь вид:

(1)

Это уравнение необходимо заменить уравнением в конечных разностях. Для этого стенку разделим на некоторое число слоев толщины ∆ х, которые пронумеруем n -1, n, n+1,…

Заменим непрерывную функцию t =f( х) ломанной линией.

Время тоже изменяем скачкообразными интервалами ∆τ и время будет отмечено индексами k, k+1, k+2,… Тогда температура в слое в момент времени обозначится

Из рисунка следует, что кривая в слое n момента времени имеет 2 наклона:

«+», «-» - показывают направления подхода к слою

Вторая производная в конечных разностях будет иметь вид:

Производная по времени в конечных разностях для слоя n запишется:

Подставляем в исходное уравнение получим:

откуда:

(2)

Множитель можно подобрать так, что он будет равен единице. Это достигается выбором величин и

Следовательно при (3)

уравнение (2) принимает вид:

Из уравнения следует, что температура слоя n в момент времени является средней арифметической из температур, прилегающих слоев n+1 и n -1 в момент времени .

Отсюда вытекает простой метод графического построения температурного поля.

Разбиваем стенку на слои причем так чтобы выполнялось условие (3)

Затем строят начальное распределение температур - 0-1-2-3-4

Соединяя т.1 с т.3. получаем 2’; соединив т.2. с т.4. получим т.3’. и т.д.

Для определения температуры в середине слоя 1 и на его поверхности в последний момент времени через промежуток необходимо найти направляющую точку А.

Ордината точки А фиксируется , а абсцисса - подкасательной .

На расстоянии проведем вспомогательную линию МN

Соединив точку О с точкой А на пересечении с МN получим т. а. Линия, соединяющая т. а. с т.2. в пересечении со средней линией слоя 1 дает т.1’. новой температурной кривой. Соединяя т.1’. с направляющей А, получим т.0’ на поверхности стенки.

Новую температурную кривую 0’ 1’ 2’ 3’ для момента времени принимаем в качестве исходного распределения для повторного цикла построения и в итоге приходят к требуемой температурной кривой 0” 1” 2” 3’’ 4”