10. Теплопередача через ребристую плоскую стенку

Необходимо найти тепловой поток через плоскую ребристую стенку безграничных размеров. Стенка оребрена со стороны меньшего коэффициента теплоотдачи.

Поскольку для ребра b»δ, то периметр полученного сечения ребер . Площадь полученного сечения ребра , следовательно

Подставим полученное значение m в предыдущем уравнении, умножив и разделив на , получим:

Здесь - критерий Био. Это отношение внутреннего термического сопротивления теплопроводности к внешнему термическому сопротивлению теплоотдачи.

Окончательно уравнение для теплопроводности потока с поверхности ребра:

Величина -называется коэффициентом эффективности ребра.

И тогда .

Теплота, отдаваемая поверхностью:

Общее количество теплоты:

или

-приведенный коэффициент теплоотдачи.

Тогда для передачи теплоты через ребристую стенку можно записать:

Отсюда:

Если тепловой поток отнести к единице поверхности, то

где-

если отнести к неоребрёной поверхности, то

Отношение оребренной поверхности к гладкой, называется коэффициентом оребрения .

Пример: и .

для плоской поверхности .

Если стенка имеет ребра с то

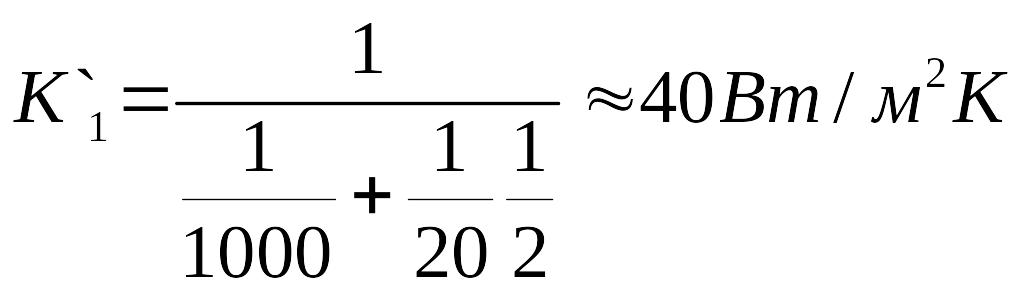
11. Нестационарные процессы теплопроводности.

Они имеют место при нагревании (охлаждении) различных заготовок и изделий, производстве стекла, обжиге кирпича, пуске и остановке различных теплообменных аппаратов.

Нестационарные тепловые процессы всегда связаны с изменением внутренней энергии или энтальпии вещества.

Охлаждение ( нагревание) неограниченной пластины

Изменение температуры не происходит в направлении y и z, т. е. . Температура изменяется только в одном направлении. Охлаждение происходит в среде с постоянной температурой, т. е. . Начальное распределение температуры задано некоторой функцией . Отсчёт температуры пластины для любого момента времени будем вести от температуры окружающей среды , т. е. .

Дифференциальное уравнение будет:

(1)

Начальные условия: при

(2)

При заданных условиях охлаждения задача становится симметричной и начало координат удобно поместить на оси пластины, при этом граничные условия запишутся на оси и поверхности:

а) на оси: при х=0 ; (3)

б) на поверхности: при x=δ

Дифференциальное уравнение, совместно с начальными и граничными условиями (1), (2), (3) однозначно формирует поставленную задачу. Методом разделения переменных ищем решение дифференциального уравнения в виде:

(4)

Решая это уравнение, получим систему обыкновенных дифференциальных уравнений, которые легко интегрируются:

(5)

(6)

(7)

(8)

подставляя данные уравнения в (4) получаем частное решение:

Выражение (9) удовлетворяет исходному уравнению (4) при любых значениях , , и .

Найдем , ,

При x=0 ,

следовательно

или ; .

обозначим =A, то уравнение (9) будет:

При x=δ , получим:

После преобразования получим: ,

где

Если , то (10)

Из анализа этого уравнения следует, что уравнение имеет бесконечное множество корней при каждом значении .

Причем

При →∞ прямая совпадет с осью абсцисса и корни уравнения будут:

; ; …

При →0 прямая совпадет с осью ординат и

Следовательно, каждому найденному значению корня будет соответствовать свое частное распределение температуры:

(11)

Общее решение можно представить:

Постоянная найдется из начальных условий:

(12)

Определяя путем разложения четной функции (12) в ряд Фурье получим:

(13), где

В безразмерной форме:

(14),

где величины - безразмерная температура; - безразмерная координата; - число Фурье, представляющее собой безразмерное время;

Анализ полученного решения.

Многочисленные исследования показали, что уже при ряд (14) становится настолько быстросходящимся, что распределение температуры достаточно точно описывается первым членом ряда:

(15)

Или:

(16)

Величина является функцией только и заранее может быть рассчитана и табулирована.

Для оси пластины cos(0) обозначим как некоторую функцию N( ) тогда (16)запишется:

(16’)

Для поверхности пластины обозначим P( ) и (16) запишется:

(16’’)

Функции N( ) и P( ) табулируемые и могут быть взяты из справочников.

Кроме того из уравнений (16’) и (16”) следует, что при заданной координате безразмерная температура является функцией двух безразмерных параметров и .

Логарифмируя (16’) и (16”) получаем:

(17)

Из (17) следует, что при заданной координате и зависит линейно от времени. Это дает возможность графически решить (16’) и (16”).