1.Теплопроводность. Закон Фурье

Теплопроводность - молекулярный перенос теплоты в телах (или между ними), обусловленный переменностью температуры в рассматриваемом пространстве.

Явление теплопроводности представляет собой процесс распространения тепловой энергии при непосредственном соприкосновении отдельных частиц тела или отдельных тел, имеющих различные температуры.

Перенос энергии в газах – путем диффузии молекул и атомов.

В жидкостях и твердых телах - диэлектриках путем упругих волн.

В металле – путем диффузии свободных электронов.

Роль упругих колебаний решетки здесь второстепенно.

Процесс теплопроводности, как и другие виды т/о может иметь место только при условии, что в различных точках тела ( или системы тел) температура не одинакова. В общем случае процесс передачи теплоты теплопроводностью в твердом теле сопровождается изменением температуры, как в пространстве, так и во времени.

Аналитические исследования теплопроводности сводятся к нахождению уравнения.

t = f(x, y, z, r ) – температурное поле - совокупность значений температуры во всех точках изучаемого пространства для каждого момента времени.

Различают стационарное и нестационарное:

Если t = f (x ,y ,r), - двухмерное

t = f (y, r ) - одномерное

Геометрическое место точек в температурном поле, имеющих одинаковую температуру называется изотермической поверхностью.

Изотермические поверхности не пересекаются.

Пересечение изотермических поверхностей плоскостью дает на этой плоскости семейство изотерм.

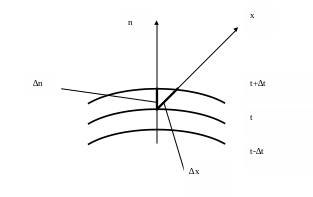
Наибольший перепад температуры на единицу длины происходит в направлении нормали к изотермической поверхности. Возрастание температуры в направление нормали к изотермической поверхности характеризуется градиентом температуры.

Градиент температуры - это вектор, направленный по нормали к изотермической поверхности, в сторону возрастания температуры и численно равный производной от температуры по этому направлению.

- единичный вектор нормальный к изотермической поверхности и направленный в сторону возрастания температуры.

Величина в направлении убывания температуры отрицательная.

; ; ;

Согласно гипотезе Фурье, количество теплоты, Дж проходящее через элемент изотермической поверхности dF за промежуток времени d пропорционально dt/dn.

λ - характеризует способность вещества проводить теплоту и называется коэффициентом теплопроводности.

Количество теплоты, проходящее в единицу времени через единичную поверхность есть плотность теплового потока: ;

Его положительное направление совпадает с направлением убывания температуры. Т.о. векторы и gradt лежат на одной прямой, но направлены в противоположные стороны. Это и объясняет наличие знака «минус» в правой части уравнения.