7.Системы ур-ний. Матричная запись системы ур-ний. Связь между решение матричного ур-ния и решением системы.
Системы линейных однородных уравнений
Уравнение
называется линейным,
если оно содержит неизвестные в первой
степени. Так, например,
есть
линейное уравнение с одним неизвестным;
-
линейное уравнение с двумя неизвестными.
Если
в исходной системе все свободные члены
равны нулю, то система называется
однородный.
Такая система всегда совместна, так
как она имеет нулевое решение:
.
Система
называется совместной,
если она имеет хотя бы одно решение:
,
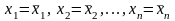и несовместной,
если она не имеет ни одного решения.
Если система совместна и имеет единственное
решение, то она называется определенной;
если же решений бесконечно много, то
система называется неопределенной.
При работе с системой принципиальным
является вопрос о ее совместности. Пусть
доказано, что система совместна. Возможны
следующие случаи:
а)
если система совместна, то есть
и число неизвестных равно рангу матриц
А и В
,
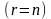то она имеет единственное решение;
б)
если же система совместна, но
,
то она имеет бесконечно много решений.
Теорема Кронекера-Капелли: Для совместности системы линейных уравнений необходимо и достаточно, что бы ранг матрицы системы был равен рангу расширенной матрицы.
8.Формулы Крамера.
Рассмотрим
частный случай системы (4), когда число
уравнений совпадает с числом неизвестных.
Пусть для определенности
,
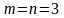то есть система имеет вид
.
Определитель
называется основным
определителем данной системы. Следующие
три определителя называются
вспомогательными:
,
,
.
Теорема
Крамера:
Если определитель матрицы А
то система имеет единственное решение
определяющееся формулами:
.
Доказательство:
АХ=B.не
трудно показать что матрица Х=
является решением данного уравнения
(
существует
т.к.определитель матрицы А
).Действительно
А(
)=В;
(
А)В=В;
ЕВ=В; В=В. Верно. Покажем, что данное
математическое уравнение имеет
единственное решение. Пусть
решение
данного уравнения, тогда
АХ=В
определяется формулой Х=
В.
То есть
=
= =
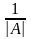
Заметим что определитель матрицы А(1);
А(1)=
А(2)=
- - - - - - - - - - - -- - - - - - - -
А(3)=
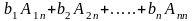
Алгебраические
дополнения последних формулах составлены
к матрицам отличных от А, но при их
нахождении столбик свободных членов
вычеркивается, поэтому они совпадают
с соответств. алгебраич. дополнением
матрицы А. Таким образом:
Замечание: При доказательстве теоремы 5 мы получили попутно способ решения систем с помощью обратной матрицы, его удобно применять если обратная матрица, матрица систем известна.
9.Метод Гаусса. Решение систем линейных уравнений. Метод Гаусса
Метод Гаусса –решение СЛУ в последовательном исключении неизвестных .
Замечание1-при решении сист. Методом Гауса работают только со строками расширенной матрицы.
Существует
общий метод решения системы из
уравнений с
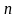неизвестными, который называется методом
последовательного
исключения
неизвестных или методом
Гаусса.Последовательное
исключение неизвестных проще и короче
проводить с помощью элементарных
преобразований
расширенной матрицы данной системы. К
ним относятся:
а) перестановка местами каких-либо строк матрицы;
б) умножение или деление (сокращение) какой-либо строки матрицы на число, отличное от нуля;
в) умножение какой-либо строки матрицы на число и прибавление к другой строке.
Очевидно, что элементарные преобразования не изменяют ранга расширенной матрицы, другими словами, не нарушают равносильности исходной системы. После ряда таких преобразований исходная матрица будет приведена к одному из следующих видов:
или
.
В
первом случае система имеет единственное
решение, во втором – либо бесконечно
много решений, если
,
либо не имеет решений, если
.