1.Матрицы. Сложение матриц и умножение на число. Их свойства.

Пусть m,n- целые положительные числа и M- непустое множество элементов любой природы. Матрицей размеров m*n над М или m*n –матрицей над M называется прям. таблица, составленная из mn элементов множества М и содержащая m строк и n столбцов.

Пусть A=(а_i,j)_m*n и B=(b_i,j)_m*n две матрицы одинаковой размерности, сумма матриц A и B, называется матрица такой же размерности, у которой каждый элемент равен сумме элементов A и B.

Произведение матрицы A=(а_i,j)_m*n на число С( С€ R),называется m*n – матрица такой же размерности, у которой каждый элемент равен произведению соотв. элемента матрицы A на число С.

1. A+B=B+A(коммунативность сложения)

2. (A+B)+C=A+(B+C)(ассоциативность)

3. A+0=A

4. A+(-A)=0

5. α(A+B)=αA+αB

6. (α+β)A=αA+βB

7. (αβ)A=α(βA)

8. 1*A=A

2. Умножение матриц, его свойства.

Пусть даны матрица A=(а_i,j)_m*n и B=(b_i,j)_n*r , у кот. число элементов в строке первой матрицы равно числу элементов в столбце второй матрицы.

Произведением матрицы А на матрицу В наз. матрица С (С=А*В=АВ) размерности m*r, у кот. каждый эл-т равен сумме произведений эл-ов соответствующих строки и столбца матриц А и В.

Свойства:

1)АВ≠ВА-умножение матриц некоммутатитвно;

2)(АВ)*С=А*(ВС)-умножение матриц ассоциативно;

3)А*(В+С)=АВ+АС

(В+С)*А=ВА+СА - умножение матриц дистрибутивно по отношению к сложению;

4)α(АВ)=(αА)В=А(αВ);

3.Определители 1-ого, 2-ого, 3-его порядка.

Определителем или детерминантом кв. матрицы 1-ого порядка наз. число, обозначаемое det A=׀A׀=׀a₁₁׀ и равное самому числу а₁₁.

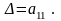
Определителем или детерминантом кв. матрицы 2 – ого порядка наз. число, обозначаемое det A=׀А׀= и равное:

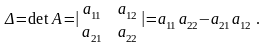
Определителем или детерминантом кв. матрицы 3-его порядка, наз. число, обозначаемое det A=׀A׀= и равное:

Определители n-го порядка. Пусть n- натуральное число, n 1 и пусть определители квадратных матриц 1,2,…, n-1 уже введены. Определителем или детерминантом квадратной матрицы 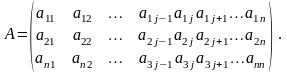порядка n наз. число, обознач.

detA= (-1)¹⁺¹ *a₁₁*M₁₁+(-1)¹⁺² *a₁₂*M₁₂+…+(-1)^1+j*a_1j*M_1j+…+ (- 1)¹⁺ⁿ*a_1n*M_1n где M_1j-определитель матрицы полученной из матриц А вычеркиванием 1-й строки и j-го столбца, j=1,2…,n.

Св-ва определителей n-го порядка:

Транспонированием матрицы А наз. такое её преобразование при кот. кажд её строка становится столбцом с тем же номером.

1)При транспонировании кв. матрицы n-го пор., её определит. не меняется.

2)Если в кв. матр.А n-ого пор. переставить местами i-тую и j-тую строки, то определитель получившейся матр. В изменит знак на противоположный (Д-во: чтобы перейти от матр.А к матр. В нужно i-тую строку последовательно переставлять с i-1,i-2,…1 при кажд. таком определитель помен. знак. Таким образом: ^i-1* .

3)Определитель кв. матр. с двумя одинаковыми строками = 0.

(Док-во: переставим в такую матрицу А одинаковые строки, матрица при этом не изменится: =- => 2* =0; =0.

4)Общий множитель элементов некоторой строки определителя можно выносить за знак определителя.

5)Если эл-ты 2-ух различных строк определителя пропорциональны, то такой определитель =0.

6)

7)Определитель n-го порядка не изменится если к элем. некоторой i-той строки прибавить соответствующие эл-ты другой j-той строки, умноженные на одно и то же число.

8)Определитель кв. матрицы n-го порядка, у которого все эл-ты некоторой строки = 0,то он = 0.

9)Определитель произведения двух кв. матриц n-го порядка = произведению их определителей:

Треугольная матрица- это кв. матрица n-го порядка, у которой все эл-ты, стоящие ниже или выше главной диагонали = 0.

10)Определитель треуг. матрицы=произв. её диагональн. эл-ов.

11)Определитель диагональной марицы = произвед. диагон.эл-ов.

12)Определитель единичной матрицы = 1.