20. Формула Тейлора. Разложение и оценка остаточного члена функции
Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема:
Экспонента:
22. Правило Лопиталя. Неопределенности различных видов. Примеры.
Правило
Лопиталя — метод нахождения пределов
функций, раскрывающий неопределённости
вида
и
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен пределу отношения
их производных.
Условия:1.
2.
3
4.
Пределы также могут быть односторонними.
Основные
виды неопределенностей:
Под неопределенностью вида понимается отношение двух бесконечно малых величин. Неопределенность вида возникает при делении одной бесконечно большой величины на другую. Остальные аналогично.
Любая
форма неопределенности может быть
преобразована к неопределенности вида
.
Действительно, пусть f(x)
и g(x)
– бесконечно большие функции в окрестности
некоторой точки. Тогда
24. Геометрическое определение выпуклости функции. Критерии выпуклости. Точки перегиба.
Непрерывная
на отрезке [a;
b]
функция f(x)
называется выпуклой вверх на этом
отрезке, если для любых точек x1
и x2
из этого отрезка
Другими словами, если для любых точек x1 и x2 отрезка [a; b] секущая AB проходит под графиком функции f(x), то функция f выпукла вверх. Аналогично определяется функция, выпуклая вниз.
Дважды
дифференцируемая на [a;
b]
функция f(x)
выпукла вверх, если для любого
Дважды
дифференцируемая на [a;
b]
функция f
(x)
выпукла вниз, если для любого
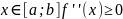
Пусть функция f(x) непрерывна в точке x0 и имеет в этой точке конечную или бесконечную производную. Тогда точка x0 называется точкой перегиба функции f, если в этой точке изменяется направление ее выпуклости.
Необходимое
условие наличия точки перегиба. Если
x0
– точка перегиба функции f(x),
и функция f(x)
имеет вторую производную, непрерывную
в этой точке, то
