10. Первый замечательный предел. Доказательство.

Доказательство:

Рассмотрим односторонние пределы и и докажем, что они равны 1.

Пусть . Отложим этот угол на единичной окружности ( ).

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке . Точка H — проекция точки K на ось OX.

Очевидно, что:

(1) (где

Подставляя в (1), получим:

Так как при

Умножаем на sinx: Перейдём к пределу:

Найдём левый односторонний предел:

Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

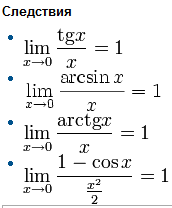
12. Определение функции, дифференцируемой в точке. Определение дифференциала функции.

Функция называется дифференцируемой в точке , если ее приращение можно представить в виде

Дифференциалом функции в точке называется главная линейная относительно часть приращения функции в этой точке и обозначается или , т.е.

14. Геометрический смысл производной и дифференциала. Уравнение касательной.

Производной функции в точке называется предел отношения приращения функции к соответствующему приращению аргумента , при условие, что .

Геометрический смысл производной:

Производная в точке равна угловому коэффициенту касательной к графику функции в точке, абсцисса которой равна .

Дифференциалом функции в точке называется главная, линейная относительно , часть приращения функции.

Покажем, что и эквивалентные бесконечно малые при :

( - бесконечно малая)

Геометрический смысл дифференциала:

Проведем к графику функции в точку 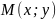касательную и рассмотрим ординату этой касательной для точки . На рисунке , . Из прямоугольного треугольника имеем: , т.е. . Но, согласно геометрическому смыслу производной, . Поэтому . или . Это означает, что дифференциал функции в точке x равен приращению ординаты касательной к графику функции в этой точке, когда x получает приращение .

Приближенные вычисления:

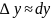
16Лемма Ферма.

Лемма Ферма утверждает, что производная дифференцируемой функции в точке локального экстремума равна нулю.

Пусть функция имеет во внутренней точке области определения локальный экстремум. Пусть также существуют односторонние производные конечные или бесконечные. Тогда

1. если x₀ — точка локального максимума, то 2)если x₀ — точка локального минимума, то

В частности, если функция имеет в производную, то

Доказательство:

Предположим, что . Тогда

Поэтому:

Если производная определена, то получаем

то есть

Замечание. Производная дифференцируемой функции в точке локального экстремума равна нулю. Её касательная в этой точке параллельна оси абсцисс. Обратное, вообще говоря, неверно.

18. Теорема Лагранжа о конечном приращении. Доказательство и геометрический смысл.

Если функция f непрерывна на отрезке [a;b] и дифференцируема в интервале (a;b), то найдётся такая точка , что

Геометрически это можно переформулировать так: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.

Доказательство: Введем функцию . Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны . Воспользовавшись упомянутой теоремой, получим, что существует точка , в которой производная функции равна нулю:

что и требовалось доказать.