2. Случайные события и случайные величины

Пример. На складе имеется 10 запасных деталей к прибору, из которых 4 изготовлены на заводе № 1. Наудачу взяли 2 детали. Найти закон распределения, математическое ожидание и дисперсию числа деталей, изготовленных на заводе № 1, среди двух нудачу выбранных.

Решение.

Введём обозначения:

А – первая взятая деталь изготовлена на заводе № 1,

В – вторая взятая деталь изготовлена на заводе № 1,

Х – число деталей, изготовленных на заводе № 1 из двух выбранных.

Очевидно событие Х=0 состоит в том, что обе детали иготовлены не на заводе № 1, следовательно и Р(Х=0) = , т.е. . Аналогично, .

Событие Х=1 равносильно событию , но можно исходить и из свойства закона распределения, что сумма всех вероятностей равнее 1. Поэтому .

Таким образом, мы получаем закон распределения деталей, изготовленных на заводе № 1.

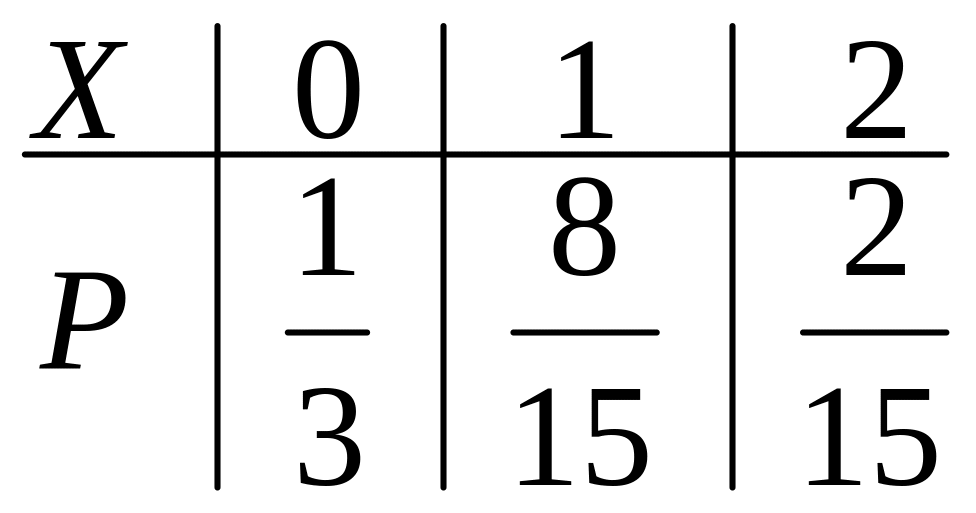
Отметим, что в данном примере вероятности можно находить и непосредственно по определению. Так как осуществляется выбор двух деталей из 10, то всего возможных исходов будет . Число исходов, благоприятных событию Х=0 - , благоприятных Х=1 это уже набор из двух множеств, т.е. и, наконец, благоприятных событию Х=2 - . Тогда

Теперь находим числовые характеристики (математическое ожидание и дисперсию).

,

,

.

Пример. Прибор №1 работает с вероятностью 0,8. а прибор №2 - с вероятностью 0,7. Найти закон распределения, математическое ожидание и дисперсию числа работающих приборов.

Решение. Обозначим:

А – работает прибор №1,

В – работает прибор № 2,

Х – число работающих приборов.

, т.к. события А и В независимы, а следовательно, независимы и противоположные им события.

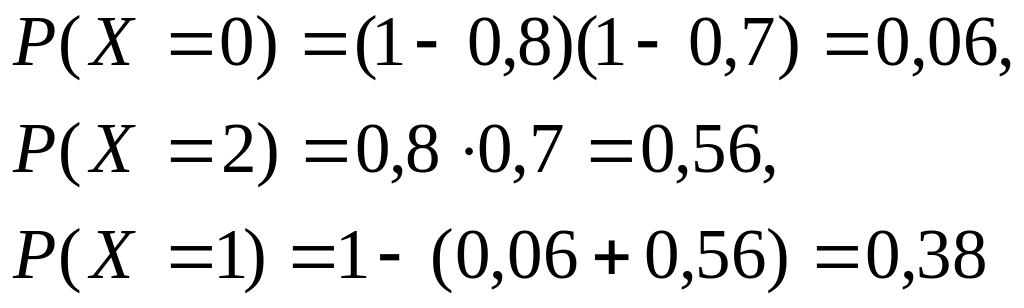
Отметим, что в этом примере непосредственный подсчёт вероятностей невозможен.

Тогда ,

Контрольная работа

1.01. В урне 4 белых и 6 красных шаров. Наудачу берут два. Найти закон распределения, математическое ожидание и дисперсию числа красных шаров, среди двух вынутых.

1.02. В урне 4 белых и 6 красных шаров. Из урны наудачу вынимают шар, фиксируют его цвет и возвращают в урну. После этого вынимают второй шар. Найти закон распределения, математическое ожидание и дисперсию числа красных шаров, среди двух вынутых.

1.03. Производится два выстрела по цели с вероятностями попадания 0,7 и 0,8. Найти закон распределения, математическое ожидание числа попаданий

1.04. Из урны, в которой 2 белых и 6 красных шаров наудачу последовательно вынимают шары пока не появится красный. Найти закон распределения, математическое ожидание и дисперсию числа вынутых шаров.

1.05. Стрелок, имеющий 3 патрона и попадающий в мишень с вероятностью 0,9 при каждом выстреле, стреляет или до первого попадания или пока не израсходует все патроны. Найти закон распределения, математическое ожидание и дисперсию числа использованных патронов.

1.06. Игрок А играет с игроком В матч из трёх партий, имея вероятность выигрыша каждой партии 0,6. Найти закон распределения, математическое ожидание и дисперсию числа побед игрока А в матче.

1.07. Приборы А и В исправны с вероятностями 0,8 и 0,9. Контролёр проверяет эти приборы. Найти закон распределения, математическое ожидание и дисперсию числа исправных приборов, обнаруженных контролёром.

1.08. Из колоды в 36 карт наудачу вынимают две. Найти закон распределения, математическое ожидание и дисперсию числа тузов среди вынутых карт.

1.09. Игрок имеет права бросать игральную кость не более трёх раз. Он бросает кость до тех пор, пока не выпадет 6 очков, или пока не использует все попытки. Найти закон распределения, математическое ожидание и дисперсию числа бросаний.

1.10. Студент к экзамену выучил 15 вопросов из 20. В билете 2 вопроса. Найти закон распределения, математическое ожидание и дисперсию числа вопросов билета, на которые студент знает ответы.

1.11. Игрок А играет с игроком В матч из трёх партий, имея вероятность выигрыша каждой партии 0,7. Найти закон распределения, математическое ожидание и дисперсию числа побед игрока А в матче.

1.12. Производится два выстрела по цели с вероятностями попадания 0,9 и 0,8. Найти закон распределения, математическое ожидание числа попаданий.

1.13. В урне 7 зелёных и 3 синих шаров. Из урны наудачу вынимают шар, фиксируют его цвет и возвращают в урну. После этого вынимают второй шар. Найти закон распределения, математическое ожидание и дисперсию числа синих шаров, среди двух вынутых.

1.14. Стрелок, имеющий 3 патрона и попадающий в мишень с вероятностью 0,7 при каждом выстреле, стреляет или до первого попадания или пока не израсходует все патроны. Найти закон распределения, математическое ожидание и дисперсию числа израсходованных патронов.

1.15. В урне 7 зелёных и 3 синих шара. Наудачу берут два. Найти закон распределения, математическое ожидание и дисперсию числа синих шаров, среди двух вынутых.

1.16. Игрок имеет права бросать игральную кость не более трёх раз. Он бросает кость до тех пор, пока не выпадет 6 очков, или пока не использует все попытки. Найти закон распределения, математическое ожидание и дисперсию числа бросаний.

1.17. Приборы А и В исправны с вероятностями 0,7 и 0,8. Контролёр проверяет эти приборы. Найти закон распределения, математическое ожидание и дисперсию числа исправных приборов, обнаруженных контролёром.

1.18. Студент к экзамену выучил 10 вопросов из 16. В билете 2 вопроса. Студент вытащил билет. Найти закон распределения, математическое ожидание и дисперсию числа вопросов билета, на которые студент знает ответы.

1.19. Из урны, в которой 2 синих и 8 красных шаров. Из урны наудачу последовательно вынимают шары пока не появится красный. Найти закон распределения, математическое ожидание и дисперсию числа вынутых шаров.

1.20. Из колоды в 52 карт наудачу вынимают две. Найти закон распределения, математическое ожидание и дисперсию числа картинок (валетов, дам или королей) среди вынутых карт.

2.01. В урне 10 шаров, из которых 4 красных.

Какова вероятность того, что из двух наудачу взятых шаров

а) ровно один красный,

в) хотя бы один красный?

2.02. В урне 5 красных 2 синих и 3 белых шаров.

Из урны последовательно вынимают три шара, не возвращая в урну.

Какова вероятность того, что будут вынуты красный, синий и белый в указанном порядке? Какова будет эта вероятность, если шар вынимают, фиксируют его цвет и возвращают в урну, после чего берут следующий шар?

2.03. В урне 14 шаров, из которых 4 красных.

Какова вероятность того, что из двух наудачу взятых шаров

а) ровно один красный,

в) хотя бы один красный?

2.04. В урне 7 красных, 2 синих и 5 белых шаров.

Из урны последовательно вынимают три шара, не возвращая в урну.

Какова вероятность того, что будут вынуты красный, синий и белый в указанном порядке? Какова будет эта вероятность, если шар вынимают, фиксируют его цвет и возвращают в урну, после чего берут следующий шар?

2.05. В урне 10 шаров, из которых 6 красных.

Какова вероятность того, что из двух наудачу взятых шаров

а) ровно один красный,

в) хотя бы один красный?

2.06. В урне 5 красных, 3 синих и 2 белых шаров.

Из урны последовательно вынимают три шара, не возвращая в урну.

Какова вероятность того, что будут вынуты красный, синий и белый в указанном порядке? Какова будет эта вероятность, если шар вынимают, фиксируют его цвет и возвращают в урну, после чего берут следующий шар?

2.07. В урне 14 шаров, из которых 6 красных.

Какова вероятность того, что из двух наудачу взятых шаров

а) ровно один красный,

в) хотя бы один красный?

2.08. В урне 7 красных, 3 синих и 4 белых шаров.

Из урны последовательно вынимают три шара, не возвращая в урну.

Какова вероятность того, что будут вынуты красный, синий и белый в указанном порядке? Какова будет эта вероятность, если шар вынимают, фиксируют его цвет и возвращают в урну, после чего берут следующий шар?

2.09. В урне 16 шаров, из которых 6 красных.

Какова вероятность того, что из двух наудачу взятых шаров

а) ровно один красный,

в) хотя бы один красный?

2.10. В урне 8 красных, 3 синих и 5 белых шаров.

Из урны последовательно вынимают три шара, не возвращая в урну.

Какова вероятность того, что будут вынуты красный, синий и белый в указанном порядке? Какова будет эта вероятность, если шар вынимают, фиксируют его цвет и возвращают в урну, после чего берут следующий шар?

2.11. В урне 14 шаров, из которых 8 красных.

Какова вероятность того, что из двух наудачу взятых шаров

а) ровно один красный,

в) хотя бы один красный?

2.12. В урне 7 красных, 4 синих и 3 белых шаров.

Из урны последовательно вынимают три шара, не возвращая в урну.

Какова вероятность того, что будут вынуты красный, синий и белый в указанном порядке? Какова будет эта вероятность, если шар вынимают, фиксируют его цвет и возвращают в урну, после чего берут следующий шар?

2.13. В урне 18 шаров, из которых 8 красных.

Какова вероятность того, что из двух наудачу взятых шаров

а) ровно один красный,

в) хотя бы один красный?

2.14. В урне 9 красных, 4 синих и 5 белых шаров.

Из урны последовательно вынимают три шара, не возвращая в урну.

Какова вероятность того, что будут вынуты красный, синий и белый в указанном порядке? Какова будет эта вероятность, если шар вынимают, фиксируют его цвет и возвращают в урну, после чего берут следующий шар?

2.15. В урне 14 шаров, из которых 10 красных.

Какова вероятность того, что из двух наудачу взятых шаров

а) ровно один красный,

в) хотя бы один красный?

2.16. В урне 7 красных, 5 синих и 2 белых шаров.

Из урны последовательно вынимают три шара, не возвращая в урну.

Какова вероятность того, что будут вынуты красный, синий и белый в указанном порядке? Какова будет эта вероятность, если шар вынимают, фиксируют его цвет и возвращают в урну, после чего берут следующий шар?

2.17. В урне 16 шаров, из которых 10 красных.

Какова вероятность того, что из двух наудачу взятых шаров

а) ровно один красный,

в) хотя бы один красный?

2.18. В урне 8 красных, 5 синих и 3 белых шаров.

Из урны последовательно вынимают три шара, не возвращая в урну.

Какова вероятность того, что будут вынуты красный, синий и белый в указанном порядке? Какова будет эта вероятность, если шар вынимают, фиксируют его цвет и возвращают в урну, после чего берут следующий шар?

2.19. В урне 22 шаров, из которых 10 красных.

Какова вероятность того, что из двух наудачу взятых шаров

а) ровно один красный,

в) хотя бы один красный?

2.20. В урне 11 красных, 5 синих и 6 белых шаров.

Из урны последовательно вынимают три шара, не возвращая в урну.

Какова вероятность того, что будут вынуты красный, синий и белый в указанном порядке? Какова будет эта вероятность, если шар вынимают, фиксируют его цвет и возвращают в урну, после чего берут следующий шар?

3.01 Функция распределения случайной величины Х имеет вид

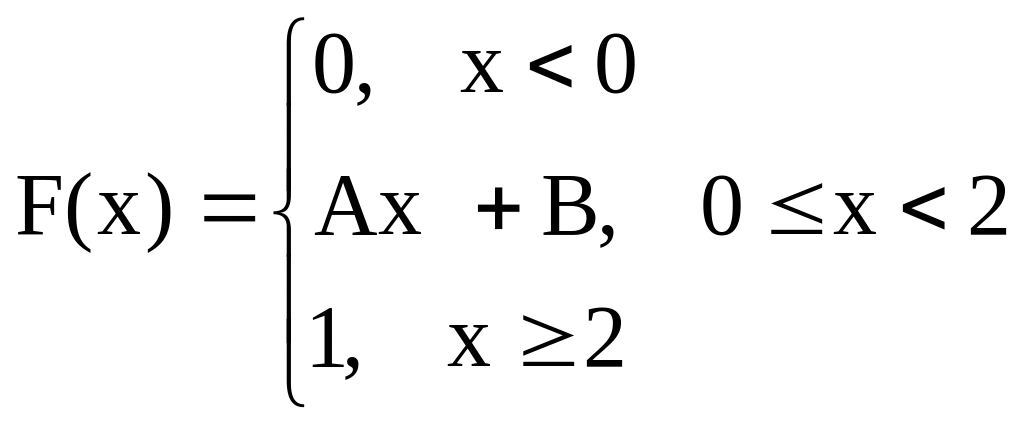
Найти А, В, плотность и .

3.02 Случайная величина и имеет плотность .

Найти К, математическое ожидание, дисперсию и функцию распределения.

3.03 Функция распределения случайной величины Х имеет вид

Найти А, В, плотность и .

3.04 Случайная величина и имеет плотность .

Найти К, математическое ожидание, дисперсию и функцию распределения.

3.05 Функция распределения случайной величины Х имеет вид

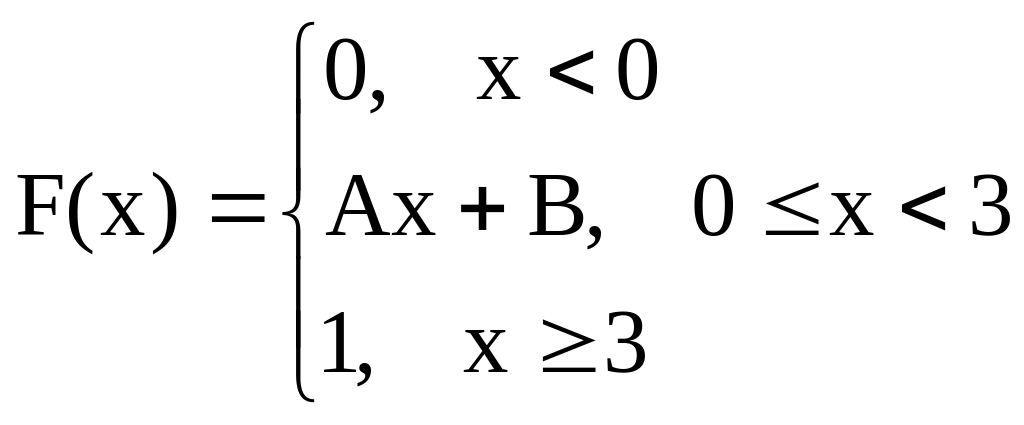
Найти А, В, плотность и .

3.06 Случайная величина и имеет плотность .

Найти К, математическое ожидание, дисперсию и функцию распределения.

3.07 Функция распределения случайной величины Х имеет вид

Найти А, В, плотность и .

3.08 Случайная величина и имеет плотность .

Найти К, математическое ожидание, дисперсию и функцию распределения.

3.09 Функция распределения случайной величины Х имеет вид

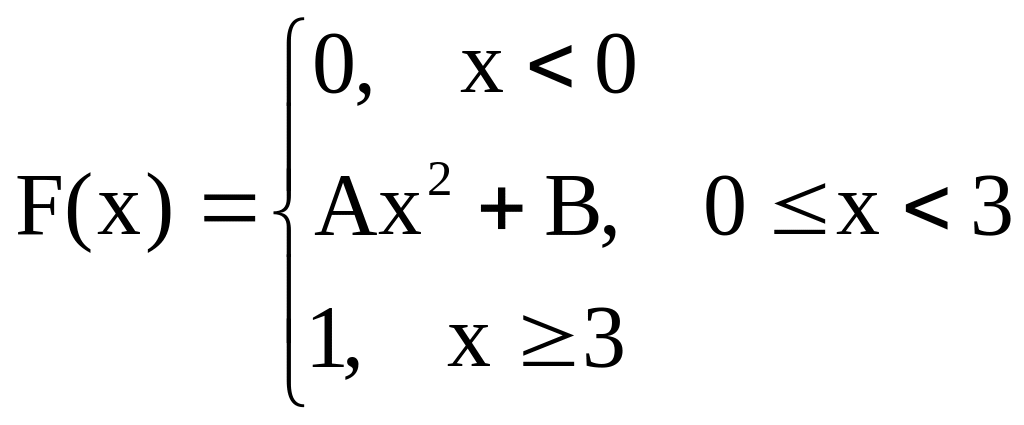
Найти А, В, плотность и .

3.10 Случайная величина и имеет плотность .

Найти К, математическое ожидание, дисперсию и функцию распределения.

3.11 Функция распределения случайной величины Х имеет вид

Найти А, В, плотность и .

3.12 Случайная величина и имеет плотность .

Найти К, математическое ожидание, дисперсию и функцию распределения.

3.13 Функция распределения случайной величины Х имеет вид

Найти А, В, плотность и .

3.14 Случайная величина и имеет плотность .

Найти К, математическое ожидание, дисперсию и функцию распределения.

3.15 Функция распределения случайной величины Х имеет вид

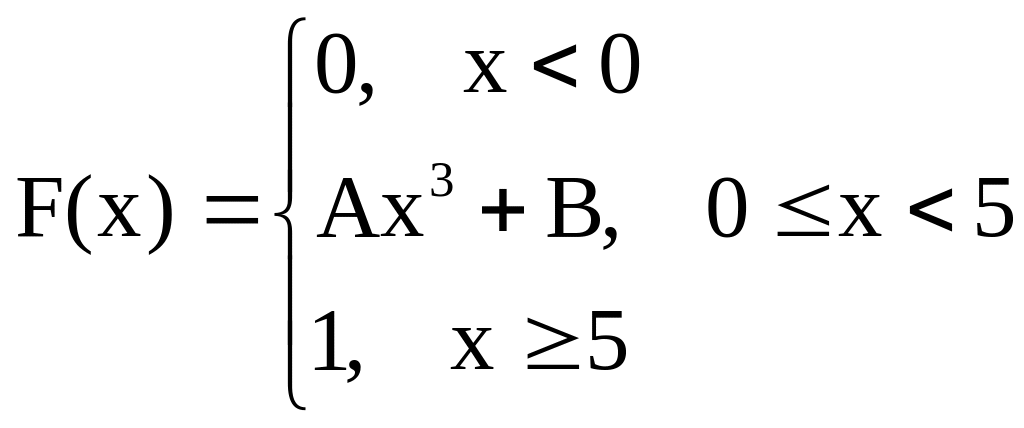
Найти А, В, плотность и .

3.16 Случайная величина и имеет плотность .

Найти К, математическое ожидание, дисперсию и функцию распределения.

3.17 Функция распределения случайной величины Х имеет вид

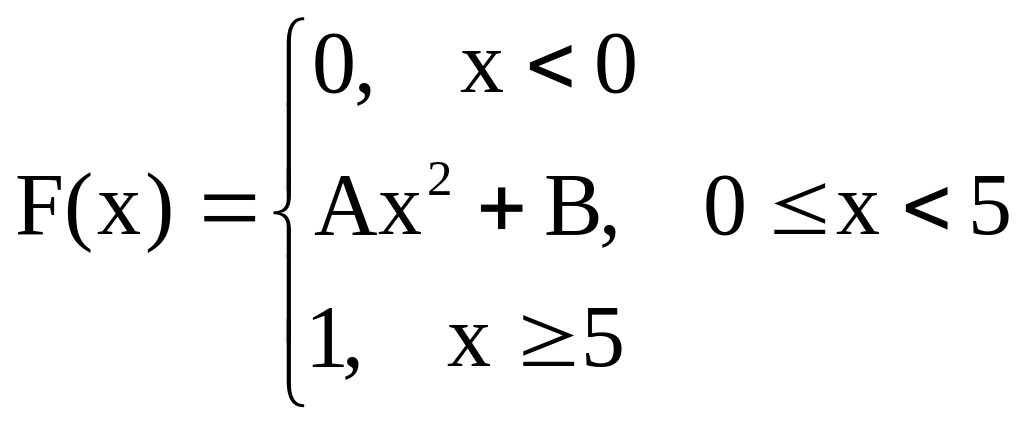
Найти А, В, плотность и .

3.18 Случайная величина и имеет плотность .

Найти К, математическое ожидание, дисперсию и функцию распределения.

3.19 Функция распределения случайной величины Х имеет вид

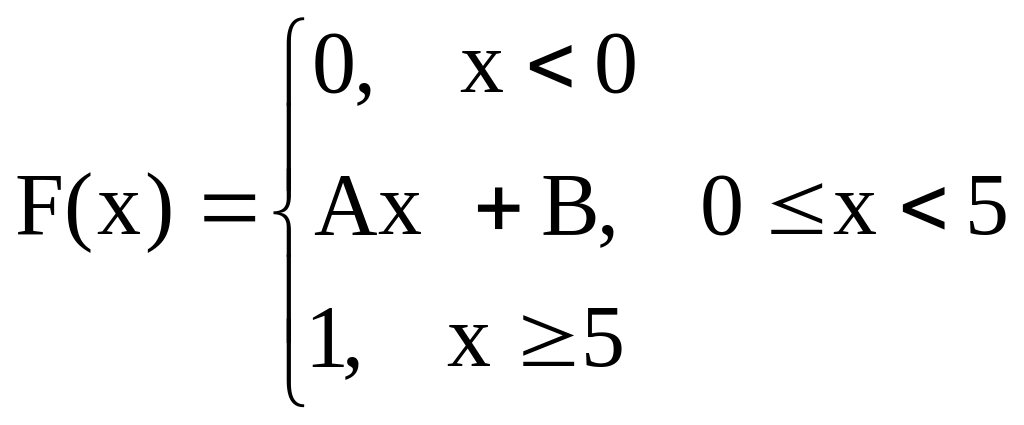
Найти А, В, плотность и .

3.20 Случайная величина и имеет плотность .

Найти К, математическое ожидание, дисперсию и функцию распределения.