Билет 26

Взаимодействие проводников с током. Закон Ампера.

Известно, что постоянный магнит оказывает действие на проводник с током (например, рамку с током); известно также обратное явление – проводник с током оказывает действие на постоянный магнит (например, на магнитную стрелку компаса) – рис.8.1.

Рис.8.1. Действие постоянного магнита на рамку с током и проводника с током на магнитную стрелку компаса.

Естественно поставить вопрос: а не может ли один проводник с током оказывать непосредственное действие на другой проводник с током? Положительный ответ на этот вопрос дал в 1820г. Ампер (Ampere A., 1775-1836), установивший силовой закон взаимодействия проводников с током.

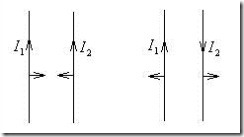
Рис.8.2. Взаимодействие двух прямолинейных проводников с током.

Так, два прямолинейных параллельных проводника (рис.8.2) притягиваются, если токи в них текут в одном направлении и отталкиваются, если токи имеютпротивоположное направление.

Для того, чтобы сформулировать закон Ампера в современном виде, введем понятие элемента тока как вектора, равного произведению силы тока I на элемент длины  проводника (рис.8.3). Элемент тока в магнитостатике играет ту же роль, что и точечный заряд в электростатике.

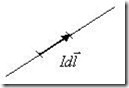
Рис.8.3. Элемент тока.

Своими опытами Ампер установил, что сила взаимодействия двух элементов тока:

1)  ;

2)  ;

3)   - зависит от взаимной ориентации элементов тока.

Объединяя эти результаты, можем написать закон Ампера в виде:

Углы θ₁ и θ₂ характеризуют ориентацию элементов тока (рис.8.4); Коэффициент пропорциональности k зависит от выбора системы единиц измерения.

Рис.8.4. Взаимодействие двух элементов тока.

В системе СИ:  , где   - магнитная постоянная.

Закон Ампера является аналогом закона Кулона в магнитостатике и выражает собой силу взаимодействия двух элементов тока. Однако в отличие от закона Кулона, он имеет более сложное написание, что обусловлено тем, что элемент тока (в отличие от точечного заряда) характеризуется не только величиной, но и направлением в пространстве. Заметим, что согласно закону Ампера   (см. рис.8.4). Это кажущееся противоречие с третьим законом Ньютона связано с тем, что в действительности мы имеем дело не с элементами токов, а с замкнутыми макроскопическими токами, для которых третий закон Ньютона выполняется.

В векторной форме закон Ампера записывается следующим образом:

.

Билет 27

Силой Лоренца называется сила, действующая на заряженную частицу, движущуюся во внешнем электромагнитном поле.

Формула для силы Лоренца (F) была впервые получена путем обобщения опытных фактов Х.А. Лоренцем в 1892 г. и представлена в работе «Электромагнитная теория Максвелла и ее приложение к движущимся телам». Она имеет вид:

 F= qE + q[VЧB],  (1)

 где q - заряженная частица;

Е - напряженность электрического поля;

B - вектор магнитной индукции, не зависящий от величины заряда и скорости его движения;

V - вектор скорости заряженной частицы относительно системы координат, в которой вычисляются величины F  и B.

 Первый член в правой части уравнения (1) - сила, действующая на заряженную частицу в электрическом поле  FЕ=qE, второй член - сила, действующая в магнитном поле:

 Fм = q[VЧB].  (2)

 Формула (1) универсальна. Она справедлива как для постоянных, так и для переменных силовых полей, а также для любых значений скорости заряженной частицы. Она является важным соотношением электродинамики, так как позволяет связать уравнения электромагнитного поля  с уравнениями движения заряженных частиц. 

В нерелятивистском приближении сила F, как и любая другая сила, не зависит от выбора инерциальной системы отсчета. Вместе с тем магнитная составляющая силы Лоренца  Fм изменяется при переходе от одной системы отсчета к другой из-за изменения скорости, поэтому будет изменяться и электрическая составляющая FЕ. В связи с этим разделение силы F на магнитную и электрическую имеет смысл только с указанием системы отсчета.

В скалярной форме выражение (2) имеет вид: 

 Fм = qVBsina,  (3)

где a - угол между векторами скорости и магнитной индукции.

 Таким образом магнитная часть силы Лоренца максимальна, если направление движения частицы перпендикулярно магнитному полю (a=p/2), и равна нулю, если частица движется вдоль направления поля В (a=0).

Магнитная сила  Fм пропорциональна векторному произведению [VЧB], т.е. она перпендикулярна вектору скорости заряженной частицы и поэтому работы над зарядом не совершает. Это означает, что в постоянном магнитном поле под действием магнитной силы искривляется лишь траектория движущейся заряженной частицы, но энергия ее всегда остается неизменной, как бы частица ни двигалась.

Направление магнитной силы для положительного заряда определяется согласно векторному произведению [VЧB] (рис. 1).

 Направление силы, действующей на положительный заряд в магнитном поле

 

 Рис. 1

 Магнитное поле В направлено к читателю перпендикулярно рисунку. Электрическое поле отсутствует.

 Для отрицательного заряда (электрона) магнитная сила направлена в противоположную сторону (рис. 2).

 Направление силы Лоренца, действующей на электрон в магнитном поле

 

 Рис. 2

 

Магнитное поле В направлено к читателю перпендикулярно рисунку. Электрическое поле отсутствует.

 Если магнитное поле однородно и направлено перпендикулярно скорости, заряд массой m движется по окружности. Радиус окружности R определяется по формуле:

 

 или  ,  (4)

 

где   - удельный заряд частицы.

 Период обращения частицы (время одного оборота) не зависит от скорости, если скорость частицы много меньше скорости света в вакууме. В противном случае период обращения частицы возрастает в связи с возрастанием релятивистской массы.

В случае нерелятивистской частицы:

 

 или  ,  (5)

 

где   - удельный заряд частицы.

 В вакууме в однородном магнитном поле, если вектор скорости не перпендикулярен вектору магнитной индукции (a№p/2 ), заряженная частица под действием силы Лоренца (ее магнитной части) движется по винтовой линии с постоянной по величине скоростью V. При этом ее движение складывается из равномерного прямолинейного движения вдоль направления магнитного поля В со скоростью   и равномерного вращательного движения в плоскости перпендикулярной полю В со скоростью   (рис. 2).

Проекция траектории движения частицы на плоскость перпендикулярную В есть окружность радиуса:

 

,

период обращения частицы:

.

 Расстояние h, которое проходит частица за время Т вдоль магнитного поля В (шаг винтовой траектории), определяется по формуле:

 h = VcosaT.  (6)

 Ось винтовой линии совпадает с направлением поля В, центр окружности перемещается вдоль силовой линии поля (рис. 3).

 Движение заряженной частицы, влетевшей под углом a№p/2  в магнитное поле В

 

 Рис. 3

 Электрическое поле отсутствует.

 Если электрическое поле E№0, движение носит более сложный характер.

В частном случае, если векторы E и B параллельны, в процессе движения изменяется составляющая скорости V11, параллельная магнитному полю, вследствие чего меняется шаг винтовой траектории (6).

В том случае, если E и B не параллельны, происходит перемещение центра вращения частицы, называемое дрейфом, перпендикулярно полю В. Направление дрейфа определяется векторным произведением [E, B] и не зависит от знака заряда.

Воздействие магнитного поля на движущиеся заряженные частицы приводят к перераспределению тока по сечению проводника, что находит свое проявление в термомагнитных и гальваномагнитных явлениях.

        Эффект открыт нидерландским физиком Х.А. Лоренцем (1853-1928).

Временные характеристики

Время инициации (log to от -15 до -15);

Время существования (log tc от 15 до 15);

Время деградации (log td от -15 до -15);

Время оптимального проявления (log tk от -12 до 3).

Диаграмма:

Технические реализации эффекта

Техническая реализация действия силы Лоренца

Техническая реализация эксперимента по прямому наблюдению действия силы Лоренца на движущийся заряд как правило довольно сложна, так как соответствующие заряженные частицы имеют молекулярный характерный размер. Поэтому наблюдение их траектории в магнитном поле требует вакуумирования рабочего объема во избежание столкновений, искажающих траекторию. Так что специально такие демонстрационные установки как правило не создаются. Легче всего для демонстрации использовать стандартный секторный магнитный масс-анализатор Ниера, см. Эффект 409005, - действие которого целиком основано на силе Лоренца.

Применение эффекта

Типичное испольтзование в технике - датчик Холла, широко используемый в измерительной технике. 

Пластинка из металла или полупроводника помещается в магнитное поле В. При пропускании через нее электрического тока плотности j в направлении перпендикулярном магнитному полю в пластине возникает поперечное электрическое поле, напряженность которого Е перпендикулярна обоим векторам j и В. По данным измерений находят В.