Псевдоконические проекции

В псевдоконических проекциях параллели изображаются дугами концентрических окружностей, один из меридианов, называемый средним — прямой линией, а остальные — кривыми, симметричными относительно среднего.

Примером псевдоконической проекции может служит равновеликая псевдоконическая проекция Бонна.

Псевдоцилиндрические проекции

В псевдоцилиндрических проекциях все параллели изображаются параллельными прямыми, средний меридиан — прямой линией, перпендикулярной параллелям, а остальные меридианы — кривыми. Причём средний меридиан является осью симметрии проекции.

Поликонические проекции

В поликонических проекциях экватор изображается прямой, а остальные параллели изображаются дугами эксцентрических окружностей. Меридианы изображаются кривыми, симметричными относительно центрального прямого меридиана, перпендикулярного экватору.

Кроме вышеперечисленных встречаются и другие проекции, не относящиеся к указанным видам.

17) локсодромия — кривая на поверхности вращения, пересекающая все меридианы под постоянным углом, называемым локсодромическим путевым углом.

Если передвигаться с фиксированным путевым углом по Земле, которую условно принять за сферу или эллипсоид, то траектория движения объекта и будет локсодромией. Локсодрома не является кратчайшим путём между двумя пунктами (исключение — меридианы и экватор). Тем не менее, в старину суда и путешественники нередко двигались по локсодромам, так как идти под постоянным углом к Полярной звезде проще и удобнее. С изобретением компаса мореплаватели перешли на движение по «магнитным локсодромам», то есть по линиям с постоянным углом к магнитному северу, что дало возможность продолжать движение и в облачную погоду. Но как только были выяснены магнитные склонения во всех местах Земли, люди вновь перешли на обычные локсодромы. Даже в XX веке локсодромия использовалась при расчёте требуемого курса при прокладке маршрута самолётов и морских судов. Со временем, когда появились приборы с достаточной вычислительной мощностью для вычисления текущего требуемого путевого угла, начали активно применять ортодромию (кратчайший путь), особенно для дальних маршрутов самолётов.

Ортодромия — кратчайшая линия между двумя точками на поверхности вращения. В картографии и навигации — название геодезической линии кратчайшего расстояния между двумя точками на поверхности земного шара, наименьший из отрезков дуги большого круга, проходящей через эти точки. В отличие от локсодромии ортодромия пересекает меридианы под разными углами. В судо- и самолётовождении, где Земля принимается за шар, ортодромия представляет собой дугу большого круга.

Экватор и меридианы являются частными случаями ортодромии. Через две точки на земной поверхности, расположенные не на противоположных концах одного диаметра Земли, можно провести только одну ортодромию.

В большинстве картографических проекций ортодромии изображаются кривыми линиями (за исключением, быть может, меридианов и экватора). Это неудобно для прокладки кратчайших маршрутов. В гномонической проекции все ортодромии изображены прямыми линиями.

Параллели (за исключением экватора) не являются ортодромиями.

локсодромия,- линия на поверхности вращения, пересекающая все меридианы под 

постоянным углом а. Если а - острый или тупой угол, то Л. образует бесконечное число витков вокруг полюса, все приближаясь к нему. Для поверхности вращения, первая квадратичная форма к-рой записана в виде 

уравнение Л.:

Для сферы с первой квадратичной формой 

уравнение Л.:

18) ЭЛЕМЕНТАРНАЯ ТЕОРИЯ МЕРКАТОРСКОЙ ПРОЕКЦИИ. ПОНЯТИЕ О ПЛАНАХ Картографическая сетка меркаторской проекции строится следующим образом. Условный глобус заключается в цилиндр, касательный глобусу по экватору (рис. 2). Меридианы, нанесен­ные на глобус, распрямляются до тех пор, пока они не коснутся внутренней поверхности цилиндра. При этом меридианы образу­ют на поверхности цилиндра ряд прямых линий, параллельных между собой. Расстояние между этими .линиями равно расстоя­ниям между меридианами на экваторе глобуса. При распрямлении меридианов параллели растягиваются и становятся равными по длине экватору. На внутренней поверхности цилиндра они обра зуют ряд окружностей   Рис2 Рис 3 . Удлинение параллелей будет тем значи­тельнее, чем ближе они к полюсу. Найдем математическую закономерность, которая определяет характер растяжения каждой параллели. Обозначим (рис. 3) радиус параллели АВ, лежащей в широте φ, через г, а радиус Земли — через R. В прямоугольном треугольнике ВОС<СВО =  Умножив левую и правую части равенства на 2л, полу­чим в левой части длину экватора, а в правой — длину парал­лели, умноженную на секанс широты данной параллели,  (*) Из выражения (*) можно сделать заключение, что любая параллель, удлиняясь до окружности экватора, растягивается пропорционально секансу широты. Разрежем цилиндр по образующей и развернем его на плос­кость. Полученная картографическая сетка удовлетво­ряет первому требованию к морской карте: так как все меридиа­ны параллельны, то локсодромия изобразится на ней прямой линией. Однако проекция не является равноугольной, поскольку участки земной поверхности при проектировании будут вытяги­ваться на ней вдоль параллелей пропорционально секансу φ и, следовательно, не будет сохраняться подобие фигур на местности и на карте, Так, небольшой остров К имеющий круглую форму,изобразится в виде эллипса, вытянутого в широтном направле­нии (см. рис. 4, а). Чтобы сделать проекцию равноугольной, необходимо теперь меридианы в каждой точке растянуть так же, как в этой точке растянулась параллель, т. е. пропорционально секансу широты точки. После этого масштаб на каждом небольшом участке карты станет одинаковым как по параллели, так и по меридиану (рис. 4, б). Изображение круглого острова на картографической сетке сохранит свою круглую форму, т. е. проекция будет обладать свойством равноугольное™. Построенная таким методом картографическая проекция, удовлетворяющая обоим требованиям к морской карте, носит название меркаторской. Масштаб полученной проекции меняется при перемене широ­ты, оставаясь постоянным по направлению параллелей. Поэтому при составлении меркаторской карты главный масштаб указы­вается по одной из параллелей. За главную параллель может приниматься средняя параллель участка земной поверхности, охватываемого данной картой. Однако при построении карт срав­нительно мелкого масштаба за главную, как правило, принима­ется стандартная параллель данного моря или широтного пояса, даже если она не проходит через карту.

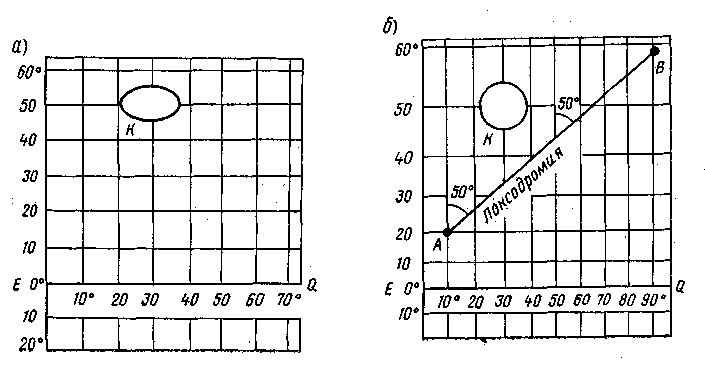
Рис. 4. Построение меркаторской проекции: с — сетка из меридианов и параллелей; б — меркаторска я проекция Чтобы было удобно измерять расстояния, а также разности широт, боковые рамки меркаторской карты разбивают на участ­ки в 1', т. е. на морские мили. Так как при построении карты меридианы вытягивались не равномерно, а пропорционально се­кансу широты в каждой точке, то морские мили будут изобра­жаться разными по длине участками, увеличивающимися по мере удаления от экватора.  Изображение 1 морской мили на меркаторской карте в дан­ной широте называется меркаторскрй милей. На экваторе, т. е. в широте 0°, меркаторская миля равна 1 экваториальной миле, в широте 60° — 2 экваториальным Милям (sec 60°.= 2), а в широте 80° — 5,8 экваториальным милям (sec 80° = 5,8). При изменении расстояния в какой-либо широте следует пользоваться меркаторскими милями, взятыми с боковой рамки карты в той же широте.