1. абсолютная погрешность и ее граница.

Абсолютная погрешность D -  это разность между измеренным X и истинным Xи значениями измеряемой величины. Абсолютная погрешность выражается в единицах измеряемой величины:    D = Х - Хи .         Поскольку истинное значение измеряемой величины определить невозможно, вместо него на практике используют действительное значение измеряемой величины Хд. Действительное значение находят экспериментально, путем применения достаточно точных методов и средств измерений. Оно мало отличается от истинного значения и для решения поставленной задачи может использоваться вместо него. При поверке за действительное значение обычно принимают показания образцовых средств измерений. Таким образом, на практике абсолютную погрешность находят по формуле      D » Х – Хд .  

2. Относительная погрешность.

Относительная погрешность измерения – это отношение абсолютной погрешности к действительному (истинному) значению измеряемой величины (часто выраженное в процентах):  = (/ х_и) 100%

3. Прямое интерполирование.

Интерполирование. в математике - один из важнейших способов приближенного вычисления. Задача И. заключается в том, чтобы по данным величинам некоторой функции для известных значений переменных независимых (аргументов) найти величину функции для произвольного (обыкновенно промежуточного) значения этих переменных независимых. Этой задачей занимались Валлис, Ньютон, Эйлер и другие математики. Найти формулу И. значит заменить искомую функцию более простой, обыкновенно многочленом, причем коэффициенты и степени этого многочлена подбираются так, чтобы значение его для данного значения переменных независимых совпадало с заданными значениями искомой функции. Формулы И. представляют выражения, в которых искомая функция представляется при помощи данных величин функции и их последовательных разностей. В нижеследующей таблице в первом столбце стоят последовательные аргументы (значения независимой переменной), во втором - соответствующие величины функции, а в следующих - последовательные разности, так что b' = а" - а, b" = а' - а"... с" = b" - b"...

5. Тригонометрические функции угла. Тригонометрические функции острого угла есть отношения различных пар сторон прямоугольного треугольника   ( рис.2 ):

6. 

1) Синус - отношение противолежащего катета к гипотенузе:  sin A = a / c .  

2) Косинус - отношение прилежащего катета к гипотенузе:  cos A = b / c .

3) Тангенс - отношение противолежащего катета к прилежащему:  tan A = a / b .

4) Котангенс - отношение прилежащего катета к противолежащему: cot A = b / a .

5) Секанс - отношение гипотенузы к прилежащему катету:  sec A = c / b .

6) Косеканс - отношение гипотенузы к противолежащему катету: cosec A = c / a .

6) Длина дуги окружности. Длина окружности

Длина окружности обозначается буквой C и вычисляется по формуле:

C = 2πR, где R — радиус окружности.

Вывод формулы, выражающей длину окружности

Путь C и C’ — длины окружностей радиусов R и R’. Впишем в каждую из них правильный n-угольник и обозначим через P_n и P'_n их периметры, а через a_n и a'_n их стороны. Используя формулу для вычисления стороны правильного n-угольника a_n = 2R sin (180°/n) получаем: P_n = n · a_n = n · 2R sin (180°/n), P'_n = n · a'_n = n · 2R' sin (180°/n). Следовательно, P_n / P'_n = 2R / 2R'. (1) Это равенство справедливо при любом значении n. Будем теперь неограниченно увеличивать число n. Так как P_n → C, P'_n → C', n → ∞, то предел отношения P_n / P'_n равен C / C'. С другой стороны, в силу равенства (1) этот предел равен 2R / 2R'. Таким образом, C / C' = 2R / 2R'. Из этого равенства следует, что C / 2R = C' / 2R', т. е. отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей. Это число принято обозначать греческой буквой π ("пи"). Из равенства C / 2R = π получаем формулу для вычисления длины окружности радиуса R: С = 2πR.

Длина дуги окружности

Так как длина всей окружности равна 2πR, то длина l дуги в 1° равна 2πR / 360 = πR / 180. Поэтому длина l дуги окружности с градусной мерой α выражается формулой

l = (πR / 180) · α.

5. Единицы измерения дуг и углов. Градус - единица измерения плоского угла, равная 1/90 части прямого угла, обозначается знаком °. 1° = 60' = 3600", где 1' — минута, 1" — секунда. Прямой угол составляет 90°, развёрнутый 180°. Г. употребляется также для измерения дуг окружности (полная окружность равна 360°).

5. Радиан как единица измерения угловых величин.

Радиа́н — основная единица измерения плоских углов в современной математике и физике. Радиан определяется как угловая величина дуги, длина которой равна её радиусу. Таким образом, величина полного угла равна 2π радиан.

Поскольку длина дуги окружности пропорциональна её угловой мере и радиусу, длина дуги окружности радиуса R и угловой величины α, измеренной в радианах, равна Rα.

Так как величина угла, выраженная в радианах, равна отношению длины дуги окружности к длине её радиуса, радиан — величина безразмерная. Поэтому обозначение радиана (рад) часто опускается.

9)Основные понятия сферической тригонометрии. Сферой. или сферической поверхностью называется геометрическое место точек в пространстве равноудаленных от некоторой точки называемой центром сферы. Радиусом сферы называется отрезок прямой соединяющий центр сферы с любой из ее точек. Всякое сечение сферы плоскостью является окружностью, которая в сферической тригонометрии часто называется кругом. Сечение проходящее через центр сферы больше всякого другого сечения. Оно называется большим кругом. Радиус большого круга равен радиусу сферы.Точки пересечения оси круга с поверхностью сферы в диаметрально противоположенных направлениях называются полюсами круга. Сферическим радиусом большого круга называется дуга другого большого круга заключенная между любой точкой данного большого круга и его полюсом. Дуга большого круга называемая в судовождении ортодромией является кратчайшем настоянием между двумя точками на сфере подобно тому, как прямая линия является кратчайшем расстоянием между двумя точками на плоскости. Сферическим треугольником называется фигура на сфере ограниченная тремя пересекающимися попарно ДБК которые не пересекаются в одной точке. В задачах решаются треугольники стороны которых не превосходят 180гр. Т.е. эти треугольники помещаются на одной половине сферы. Сумма сторон сферического треугольника находится в приделах 0<a+b+c<a+b+c По форме сферические треугольники разделяют на косоугольные прямоугольные и четвертные или прямостороннии. Два сферических треугольника, у которого вершины одного являются полюсами сторон другого называются взаимно полярными треугольниками.  Противолежащие стороны и углы двух взаимно полярных треугольников дополняют друг друга до 180.</a+b+c

Сферой называется геометрическое место точек пространства, расположенных на данном расстоянии от данной точки, называемой её центром. Отрезок, соединяющий центр сферы с какой-либо его точкой, называется радиусом сферы. Отрезок, соединяющий де точки сферы и проходящий, кроме того, через его центр, называется диаметром. Из определения следует, что все радиусы равны и что диаметр равен удвоенному радиусу. Плоскость, проходящая через центр сферы, называется диаметральной плоскостью. Пусть S-некоторая сфера с центром O радиуса R. Возьмём плоскость , удалённую от точки O на расстояние, меньшее R. Тогда пересечения плоскости  и сферы S есть окружность. Радиус r этой окружности является катетом прямоугольного треугольника (рис.1), гипотенуза которого – радиус R, а второй катет – перпендикуляр h, опущенный из центра сферы на плоскость. Поэтому в силу теоремы Пифагора r = 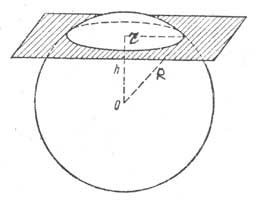Рис 1 Эта формула показывает, что величина r принимает максимальное значение r=R при h=0, то есть является диаметральной плоскостью. В этом случае окружность на сфере и называется большой окружностью. В геометрии на сфере большие окружности играют роль прямых на плоскости. При h>0 мы имеем rмалой окружностью. Так как через всякие три точки пространства, не лежащие на одной прямой, проходит единственная плоскость, то через всякие две точки сферы, не являющиеся диаметрально противоположными проходит единственная диаметральная плоскость. Поэтому через всякие две точки сферы, не являющиеся диаметрально противоположными, проходит единственная большая окружность (рис.2). Этот факт вполне аналогичен тому, что на плоскости через всякие две точки проходит единственная прямая. Через две диаметрально противоположные точки сферы, напротив, можно провести бесконечное множество больших окружностей (рис.3). Так как всякие две диаметральные плоскости сферы пересекаются по её диаметру, то всякие две большие окружности пересекаются в двух диаметрально противоположных точках сферы (рис.4). Здесь мы наблюдаем отличие сферической геометрии от плоской геометрии, в которой две прямые пересекаются не более чем в одной точке. 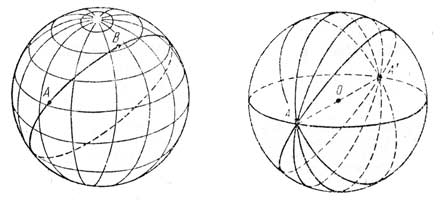Рис 2 Рис 3 Так как плоскость делит пространство на две области, то большая окружность делит сферу на две области (рис.2); эти области называются полусферами, а сама окружность – краем этих полусфер. Далее, так как две пересекающееся плоскости делят пространство на четыре области, то две большие окружности делят сферу на четыре области (рис.4). Наконец, так как три плоскости, пересекающиеся в одной точке, делят пространство на восемь областей, то три большие окружности, не пересекающиеся в одной точке, делят сферу на восемь областей (на рис.5) изображены восемь областей ABC, ABC, ABC, ABC, ABC, ABC, ABC, ABC, на которые делят сферу большие окружности AB, AC и BC, причём точки A,B,C диаметрально противоположны точкам A,B,C и, следовательно, области ABC и ABC, ABC и ABC, ABC и ABC, ABC и ABC попарно диаметрально противоположны). 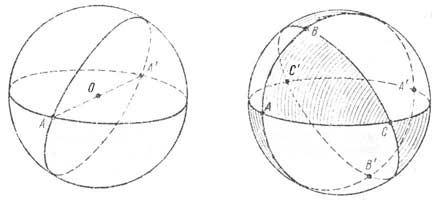Рис 4 Рис5 Если первые два из этих свойств аналогичны свойствам прямых на плоскости, которая делится на две области прямой и на четыре области двумя пересекающимися прямыми, то третье из указанных свойств не вполне аналогично соответствующему свойству прямых на плоскости, так как три попарно пересекающиеся прямые, не проходящие все три через одну точку, делят плоскость не на восемь, а на семь частей (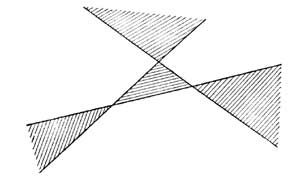рис.6). Рис 6.

10) решение сферических навигационных треугольников расчет расстояния между точками

Расстояние между двумя точками на земном шаре

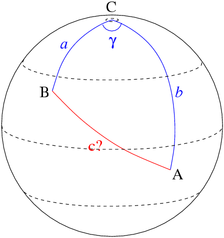
Надо вычислить расстояние между двумя точками на земном шаре:

Точка A: широта   долгота 

Точка B: широта   долгота 

Рассмотрим сферический треугольник  , где   — северный полюс. Для него известны следующие величины:

Это случай «две стороны и угол между ними». Из приведенных там формул получаем:

,

Здесь   — радиус земли

12)

Гео́ид (буквально — «нечто подобное Земле») — геометрическое тело, отражающее свойства потенциала силы тяжести на Земле (вблизи земной поверхности). Геоид определяется как эквипотенциальная поверхность земного поля тяжести (уровенная поверхность), приблизительно совпадающая со средним уровнем вод Мирового океана в невозмущённом состоянии и условно продолженная под материками. Отличие реального среднего уровня моря от геоида может достигать 1 м.

По определению эквипотенциальной поверхности, поверхность геоида везде перпендикулярна отвесной линии.

Земной сфероид - геометрическая фигура, близкая к шару, слабо сплюснутому в направлении полюсов, и наилучшим образом представляющая фигуру геоида, т. е. фигуру Земли в целом. В простейшем случае сфероид совпадает с эллипсоидом вращения и является фигурой равновесия однородной жидкой массы, все частицы которой взаимно притягиваются по закону всемирного тяготения и которая вращается с постоянной угловой скоростью около неизменной оси. Хотя Земля не является однородной жидкой массой, всё же З. с. мало отличается от соответствующего эллипсоида вращения. Отклонение поверхности З. с. от поверхности земного эллипсоида наибольшее под широтой 45° — около 3—4 м. Вследствие этого в геодезии фигуру геоида обычно заменяют эллипсоидом вращения с соответствующими размерами полуосей и определённым положением в теле Земли и все геодезические задачи решают на поверхности такого эллипсоида.

Референц-эллипсоид (от лат. referens – сообщающий, вспомогательный) – земной эллипсоид, с определёнными размерами и положением в теле Земли, служащий вспомогательной математической поверхностью, к которой приводят результаты всех геодезических измерений на земной поверхности и на которую тем самым проектируются пункты опорной геодезической сети.

Референц-эллипсоид наилучшим образом согласуюется с поверхностью геоида на ограниченной части его поверхности.

Требования к референц-эллипсоиду:

1)Ось вращения должна быть параллельна оси вращения Земли 2)Плоскость экватора должна быть параллельна плоскости Земного экватора

14) Масштабы.

Числовой масштаб — дробь, числитель которой — единица, а знаменатель — число, показывающее, скольким единицам длины на местности равна единица длины на карте. Например, дробь 1/200000 означает, что одной единице длины на карте соответствует 200 000 таких же единиц длины на местности (1 см на карте равен 200 000 см на местности и т. п.).  Линейный масштаб указывает, какое число более крупных единиц расстояния на местности содержится в одной более мелкой единице на карте (например, 5 миль в 1 см).  Для перехода от числового масштаба к линейному знаменатель числового масштаба делят на длину морской мили, выраженную в тех единицах, к которым приводится линейный масштаб. Например, числовой масштаб 1/200000, тогда линейный масштаб будет 200000/185200 = 1,03 мили в 1 см.  Для перехода от линейного масштаба к числовому линейную длину изображения одной мили на карте делят на длину морской мили в тех же единицах, в которых длина мили дана на карте. Например, линейный масштаб 5 миль в 1 см, тогда числовой масштаб 1/51852100 = 1/926000.

 Предельная точность масштаба различна у карт с различными масштабами. Так, например, если имеется карта с масштабом 1:200 000, т.е . 1 мм на карте соответствует. 200 м на местности, тогда предельная точность масштаба будет 0,2X200 — 40 м. Морские карты печатают на листах стандартных размеров, поэтому если необходимо изобразить на карте определенный район, то масштаб определяют в соответствии с предельными размерами листа меркаторской карты.