1 Формальная логика как наука. Предмет логики.

Логика (от греческого слова logos – мысль, слово, разум, закономерность)

– наука о формах, методах и законах правильного мышления.

– совокупность правил, которым подчинен процесс мышления,

– любые закономерности (логика событий, логика поступков и т.п.).

Предметом логики

является абстрактное или понятийное мышление, взятое в аспекте его формальной правильности и познавательной продуктивности.

2.Формы абстрактного мышления

Теоретическое познание – познание на основе абстрактно-понятийного отображения реальности в мыслительных формах.

Особенности теоретического познания обусловлены спецификой абстрактного мышления – опосредованный характер отражения мира, отображение предметов и явлений в обобщенной форме, активный характер отражения, взаимосвязанность с языком.

Формы теоретического познания (формы абстрактного мышления):

– понятие – это форма мышления, в которой отражаются существенные признаки отдельного предмета или группы сходных предметов; понятия – это слова или словосочетания, обозначающие какой-либо предмет или предметы, явления, состояния, процессы и т. п.;

– суждение – форма мышления, в которой что-либо утверждается или отрицается о существовании предметов, об их свойствах и об отношениях между предметами; суждения – это высказывания о предметах и явлениях;

– умозаключение – форма мышления, в которой из имеющегося исходного знания на основании определенных правил выводится новое знание; умозаключение – это рассуждение на основе имеющегося знания, результатом которого оказывается новая информация о предмете или явлении.

4.понятие логической формы.Формальная правильность и истинность мысли

Логической формой конкретной мысли называется способ связи ее составных частей, или ее структура.

Логическим законом называется необходимая, устойчивая и существенная связь между единицами мысли.

Формально-логические законы:

– закон тождества – всякая мысль должна быть тождественная самой себе;

– закон противоречия – нельзя одновременно что-либо утверждать и отри­цать об одном и том же предмете, взятом в одном и том же отношении;

– закон исключенного третьего – из двух противоречащих суждений одно истинно, а другое ложно и третьего не дано;

– закон достаточного основания – всякая истинная мысль должна быть обоснована.

Законы тождества, противоречия и исключенного третьего были сформулированы Аристотелем (384-347 гг. до н. э.), закон достаточного основания – Г. В. Лейбницем (1646-1716 гг.).

8.Логическая структура понятия.Закон обратного отношения между объемом и содержанием

В логическую структуру понятия входят объем и содержание.

Содержание понятия – совокупность признаков одноэлементного класса или класса однородных предметов, отраженных в этом понятии. В понятии должны быть отражены такие необходимые признаки, которые в совокупности позволяют отличить обозначаемый предмет от всех остальных предметов и объединить однородные предметы в класс.

Объем понятия – вся совокупность предметов, мыслимых в данном понятии или вся совокупность предметов, которые могут быть обозначены данным понятием.

Взаимосвязь содержания и объема понятия подчинена закону обратного отношения, согласно которому чем шире содержание понятия, тем уже его объем и наоборот.

7. Логические приемы формирования понятия:

– анализ – мысленное расчленение целого на части или выделение признаков;

– синтез – мысленное объединение частей в целое или присвоение признаков;

– сравнение – мысленное установление сходства или различия предметов по существенным или несущественным признакам;

– абстрагирование – мысленное выделение одних признаков и отвлечение от других (как правило, выделяются существенные признаки);

– идеализация – мысленное выделение некоторых признаков и последующая их абсолютизация, или приписывание предмету таких свойств (степеней свойств), которые невозможны в реальности;

– обобщение – мысленное объединение однородных предметов в некоторый класс.

6.Понятие как форма мышления .Языковые способы выражения понятий

Понятие – форма мышления, отображающая существенные признаки одноэлементного класса или класса однородных предметов. В языке понятия выражаются словами и словосочетаниями.

12.Определение понятия ,его логическая структура и виды.

Определение – логическая операция раскрытия содержания понятия. В логическую структуру определения входят определяемое – Dfd (от лат. definiendum) и определяющее – Dfn (от лат. definience).

Виды определений:

1. По форме определения делятся на явные и неявные:

– явные – определения, в которых даны определяемое и определяющее;

– неявные – определения, в которых дано только определяемое, а определяю­щее заменяется контекстом, набором аксиом и т. д.

2. По характеру определения делятся на реальные и номинальные:

– реальные – определения, в которых перечисляются признаки предмета;

– номинальные – в которых, посредством перечисления признаков, определяется значение термина, обозначающего понятие.

Самый распространенный вид реального определения – определение через ближайший род и видовое отличие – в этом определении сначала выделяется родовой признак, позволяющий отнести данный предмет к более широкому кругу предметов, затем выделяются видовые признаки, позволяющие отграничить данный предмет в рамках рода.

Разновидностью определения через ближайший род и видовое отличие является генетическое определение, в котором указывается способ возникновения или создания данного предмета.

13. Правила определения:

13.Правила и ошибки определения:

1)определение должно быть соразмерным – объемы определяемого и определяющего должны быть тождественны;

Логические ошибки в определении:

а) широкое определение(Лошадь — млекопитающее и позвоночное животное)

б) узкое определение(Совесть — это осознание человеком ответственности перед самим собой за свои действия и поступки)

в) определение в одном отношениии широкое, в другом — уз­кое. (Бочка — сосуд для хранения жидкостей)

2) определение не должно содержать круга – определяющее не должно содержать определяемого понятия и его содержание не должно раскрываться через определяемое;

Тавтологий(ошибка)-Круг возникает когда определяемое понятие харак­теризуется через него же, лишь выраженное иными словами, (или определяемое понятие включается в определяющее поня­тие в качестве его части).

3) определение должно быть четким и ясным – определяющее должно иметь четкий объем и ясное содержание;

Не являются правильными определениями следуют суждения: “Лень - мать всех пороков”; “Природа - это наука, способствующая пониманию вопросов, относящихся к духовной истине”

4)Определение не должно быть отрицательным.

20.Отношения между простыми суждениями по значениям истинности. «Логический квадрат»

Отношения между суждениями:

Суждения делятся на сравнимые (имеют общий S или P) и не сравнимые (не имеют общих S и P).

Сравнимые суждения делятся на совместимые и не совместимые.

Виды совместимости:

– эквиваленция – или тождество;

– субординация – или подчинение;

– субконтрарность – или частичное совпадение.

Виды несовместимости:

– контрарность – или противоположность;

– контрадикторность – или противоречие.

Логический квадрат – схематическое изображение отношений между простыми категорическими суждениями по значениям истинности.

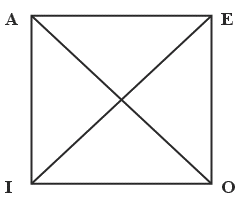
A – I и E – O – отношения подчинения – если общее суждение истинно, то частное тоже истинно, если общее суждение ложно, то частное суждение неопределённо; если частное суждение истинно, то общее неопределённо, если частное суждение ложно, то общее тоже ложно.

A – E – отношения контрарности – суждения могут быть одновременно ложными, если одно суждение истинно, то другое ложно, если одно суждение ложно, то другое неопределённо.

I – O – отношения субконтрарности – могут быть одновременно истинными – если одно суждение истинно, то другое неопределённо, если одно суждение ложно, то другое истинно.

A – O и E – I – отношения контрадикторности – если одно суждение истинно, то другое ложно и наоборот (закон исключённого третьего).

22. отрицание простых и сложных суждений .Законы де Моргана

Отрицание простых и сложных суждений – логическая операция перехода от данного суждения к противоположному суждению.

Отрицание простых суждений осуществляется либо посредством внешнего указания на ложность данного суждения («Неверно, что…»), либо посредством перехода к противоположному суждению (корректно в отношении общеутвердительных и общеотрицательных суждения).

Отрицание сложных суждений осуществляется по следующим формулам:

 (a  b)  a  b;

 (a  b)  a  b;

 (a  b)  a  b;

 (a  b)  a  b.

Формулы отрицания сложных конъюнктивных и дизъюнктивных суждений называются законами де Моргана.

21.Сложное суждения и его виды. Семантика логических союзов.

Сложными называются суждения, содержащие более одного S или более одного P.

Виды сложных суждений: в зависимости от основного логического союза (константы) сложные суждения могут быть конъюнктивными (), дизъюнктивными (), строго дизъюнктивными (), импликативными () и эквивалентными ().

Условиями истинности логических союзов называются значения истинности входящих в сложное суждение простых суждений, при которых данное сложное суждение является истинным.

Конъюнкция истинна только в том случае, если истинны оба члена сложного конъюнктивного суждения.

Дизъюнкция истинна в тех случаях, когда истинным является хотя бы один из членов сложного дизъюнктивного суждения.

Строгая дизъюнкция истинна в тех случаях, когда истинным является только один из членов сложного дизъюнктивного суждения.

Импликация истинна во всех случаях, кроме одного – когда истинна причина, но ложно следствие.

Эквиваленция истинна в тех случаях, когда совпадают значения истинности членов сложного эквивалентного суждения.

Сводная таблица истинности логических союзов:

a	b	a  b	a  b	a  b	a  b	a  b
и	и	и	и	л	и	и
и	л	л	и	и	л	л
л	и	л	и	и	и	л
л	л	л	л	л	и	и

Отрицание не является логическим союзом, это знак логической операции, заключающуюся в изменении исходных значений истинности переменной на противоположные (см. таблицу).

a	a
и	л
л	и