3. Критерий согласия Пирсона.

В математической статистике гипотезу о принадлежности закона распределения к нормальному называют основной (нулевой) гипотезой. Статистическую проверку этой гипотезы по выборке производят при помощи критериев согласия. Такие критерии позволяют определить вероятность того, что при выполнении предполагаемого закона распределения наблюдающиеся в выборке отклонения от этого закона являются случайными, а не свидетельствуют об ошибочности гипотезы. Если такая вероятность велика, то отклонения от предполагаемого закона признаются случайными, а нулевая гипотеза о законе распределения не опровергается.

В исследовательской практике применяются самые различные критерии согласия, которые оформлены в виде государственных стандартов (напр., ГОСТ 11.006-74 “Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим”).

Проверка основной гипотезы с применением критериев согласия необходима чаще всего для обоснования возможности принятия тех или иных статистических решений. Наибольшее применение получили критерии согласия Колмогорова, Пирсона, Смирнова и др. Среди них наиболее общим, применяющимся для проверки не только нормального закона, но и других, является критерий Пирсона или критерий ² (“хи - квадрат”).

В основе метода сравнения по критерию ² лежит сравнение фактически наблюдаемых частот с теоретическими, которые вычисляются в предположении нормального распределения. Как правило, эти частоты отличаются друг от друга.

Теоретические частоты вычисляются с применением функции Лапласа (интеграла вероятности) Ф₀(Z), где Z - нормированная переменная, определяемая по формуле:

Z_i = (X_i - M) /  .

В этой формуле М - математическое ожидание,  - стандартное отклонение. Наименьшее значение Z_i = Z₁ получают равным - , а наибольшее + . Тогда теоретические вероятности попадания в i-тый интервал (теоретические частости) вычисляются по следующей формуле:

. (5)

После того, как полученные значения теоретических вероятностей попадания умножим на объем выборки N, получим значения теоретических частот. Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты. При уровне значимости  требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально. Уровень значимости  - это вероятность ошибочно отвергнуть нулевую гипотезу, когда она верна.

В качестве критерия для сравнения теоретических и фактических частот (а тем самым - проверки основной гипотезы) используют случайную величину:

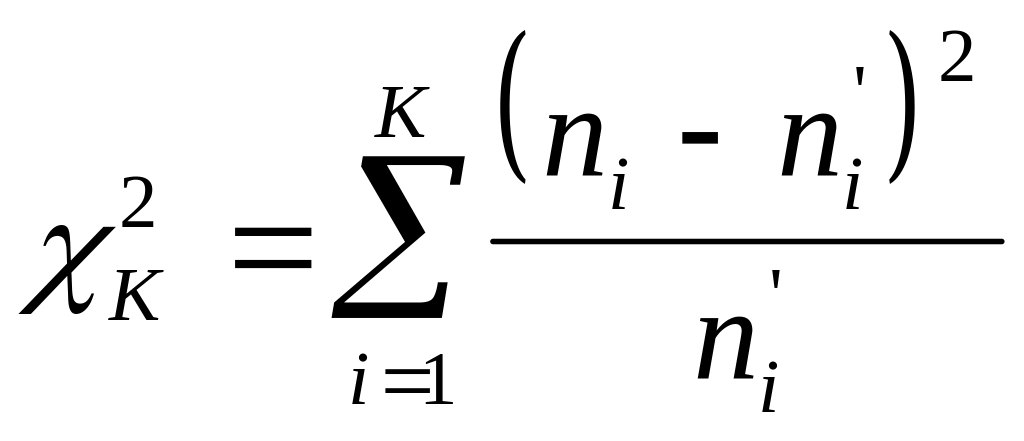, (6)

где через обозначены теоретические частоты попадания в интервал, а К - означает число интервалов. Случайной эта величина является вследствие случайности выборки и значений фактических частот . Чем ближе друг к другу фактические и теоретические частоты для каждого интервала, тем меньше величина , а это служит признаком близости фактического и предполагаемого законов распределения.

Правило проверки нулевой гипотезы следующее. Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу Н₀ , надо вычислить теоретические частоты, а затем наблюдаемое значение критерия , и по таблице критических точек распределения , (приложение 2) по заданному уровню значимости  и числу степеней свободы S найти критическую точку _КР² (;S). Если  _КР² (;S) - нет оснований отвергнуть нулевую гипотезу, если же  _КР² (;S) - нулевую гипотезу отвергают.

Уровень значимости чаще всего берут равным 0,05 (т.е. доверительная вероятность Р_ДОВ =1-  = 0,95). Число степеней свободы находят по равенству S = K - 1 - r, где К - число интервалов выборки, r - число параметров предполагаемого распределения, которые оценены по данным выборки.

В нашем случае, для предполагаемого нормального распределения мы оцениваем два параметра - математическое ожидание М и стандарт , поэтому r = 2 и число степеней свободы S = K - 3. При использовании критерия объем выборки должен быть достаточно велик, во всяком случае не менее 50. Каждый интервал частот должен содержать не менее 5 - 8 значений, малочисленные частоты объединяют, увеличивая для них интервал.

Поскольку возможны ошибки первого и второго рода, в особенности, если согласование теоретических и фактических частот “слишком хорошее”, следует проявлять осторожность. Например, можно увеличить число наблюдений, воспользоваться другими критериями, вычислить асимметрию и эксцесс и т. д.