
- •1.Основные разделы теории управления для решения производственных и социально-экономических задач.
- •2.Место теории менеджмента в теории управления.
- •3.Особенности применения теории управления для физических, производственных и социально-экономических объектов и процессов.
- •4. Понятие управления по отклонению и по возмущению для физических, производственных и социально-экономических объектов и процессов.
- •5. Разомкнутые и замкнутые системы управления для физических, производственных и социально-экономических объектов и процессов.
- •6. Обратная связь при управлении для физических, производственных и социально-экономических объектов и процессов.
- •7. Стратегия и тактика управления для физических, производственных и социально-экономических объектов и процессов.
- •8. Организационные структуры управления для физических, производственных и социально-экономических объектов и процессов.
- •9. Информационная составляющая процессов управления для физических, производственных и социально-экономических объектов и процессов.
- •10. Методы описания процессов управления для физических, производственных и социально-экономических объектов и процессов.
- •16.Принципы регулирования и стабилизации для физических, производственных и социально-экономических объектов и процессов.
- •Принципы инвариантности и автономности для физических, производственных и социально-экономических объектов и процессов.
- •26. Элементы теории игр в задачах управления для физических, производственных и социально-экономических объектов и процессов. Стратегия и тактика.
- •Методы планирования эксперимента для физических, производственных и социально-экономических объектов и процессов.
- •Фильтрация и прогнозирование. Построение линии тренда и интерполяция информации для физических, производственных и социально-экономических объектов и процессов.
- •Кибернетика как раздел теории управления
- •Технические средства управления, обработки и передачи информации для физических, производственных и социально-экономических объектов и процессов.
Нелинейное управление
Теория катастроф Одной из главных задач теории катастроф является получение так называемой нормальной формы исследуемого объекта (дифференциального уравнения или отображения) в окрестности «точки катастрофы» и построенная на этой основе классификация объектов.
Адаптивное управление Cовокупность методов теории управления, позволяющих синтезировать системы управления, которые имеют возможность изменять параметры регулятора или структуру регулятора в зависимости от изменения параметров объекта управления или внешних возмущений, действующих на объект управления. Применяется для управления нелинейной системой, и или системой с переменными параметрами. К примерам таких систем относят, например, асинхронные машины, транспортные средства на магнитной подушке, магнитные подшипники и т.п. Среди механических систем можно назвать инверсный маятник, подъемно транспортные машины, роботы, шагающие машины, подводные аппараты, самолеты, ракеты, многие виды управляемого высокоточного оружия и т.п.
Построение оптимальных робастных регуляторов Робастность означает малое изменение выхода замкнутой системы управления при малом изменении параметров объекта управления. Системы, обладающие свойством робастности, называются робастными (грубыми) системами. Обычно робастные контроллеры применяются для управления объектами с неизвестной или неполной математической моделью, и содержащими неопределённости. Главной задачей синтеза робастных систем управления является поиск закона управления, который сохранял бы выходные переменные системы и сигналы ошибки в заданных допустимых пределах несмотря на наличие неопределённостей в контуре управления.
Игровые методы в управлении Под деловыми играми следует понимать те виды игр, которые связаны с распределением ролей, игр, в ходе которых как бы проигрывается деловая ситуация.
Интеллектуальное управление Методы управления, которые используют различные подходы искусственного интеллекта, такие как искусственные нейронные сети, нечеткая логика, машинное обучение, эволюционные вычисления и генетические алгоритмы.
11. Основные свойства систем управления для физических, производственных и социально-экономических объектов и процессов. Управляемость и наблюдаемость.
Для многих систем, представленных в форме пространства состояний, эти понятия позволяют решать задачи о переводе объекта из одного состояния в другое, а также определение информации о его переменных состояний за конечное время. Управляемость Управляемость – это свойство объекта управления переходить из заданной начальной точки в заданную конечную точку за конечный интервал времени. Для линейных стационарных систем это свойство может быть определено следующим образом: Пусть линейная стационарная система задана уравнением вида:
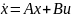 ,
где A
и
B
–
матрицы коэффициентов соответственно
при векторах состояния и управления,
причем
,
где A
и
B
–
матрицы коэффициентов соответственно
при векторах состояния и управления,
причем
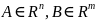 .
Тогда
система называется вполне управляемой,
если для любой точки
.
Тогда
система называется вполне управляемой,
если для любой точки
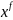 из
из
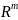 существует допустимое управление на
конечном интервале времени
существует допустимое управление на
конечном интервале времени
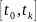 ,
переводящее систему из точки
,
переводящее систему из точки
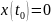 в точку
в точку
 ,
или если для любой точки
,
или если для любой точки
 существует допустимое управление на
конечном интервале времени
,
переводящее систему из состояния
существует допустимое управление на
конечном интервале времени
,
переводящее систему из состояния
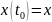 в состояние
в состояние
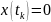 .
Критерий
управляемости.
Пусть
А
и
В
постоянны.
Рассмотрим матрицу управляемости:
.
Критерий
управляемости.
Пусть
А
и
В
постоянны.
Рассмотрим матрицу управляемости:
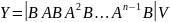 Она
состоит из столбцов матрицы В
и
произведений матриц
Она
состоит из столбцов матрицы В
и
произведений матриц
 и имеет размерность nxn,
тогда система вполне управляема тогда
и только тогда, когда ранг матрицы
управляемости равен
n.
Наблюдаемость.
Наблюдаемость
– свойство
системы, когда по выходу переменных
состояния можно полностью восстановить
информацию о состоянии системы.
Рассмотрим
линейную стационарную систему
и имеет размерность nxn,
тогда система вполне управляема тогда
и только тогда, когда ранг матрицы
управляемости равен
n.
Наблюдаемость.
Наблюдаемость
– свойство
системы, когда по выходу переменных
состояния можно полностью восстановить
информацию о состоянии системы.
Рассмотрим
линейную стационарную систему
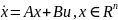
 Тогда
система вполне или полностью наблюдаема,
если существует такое
Тогда
система вполне или полностью наблюдаема,
если существует такое
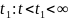 ,
что по данным измерения y(τ)
и
u(τ)
на интервале t<τ<
,
что по данным измерения y(τ)
и
u(τ)
на интервале t<τ<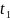 ,
можно определить состояние x(t).
Полная
наблюдаемость предлагает возможным
определить x(t)
по будущим значениям y(t)
Введем
матрицу наблюдаемости:
,
можно определить состояние x(t).
Полная
наблюдаемость предлагает возможным
определить x(t)
по будущим значениям y(t)
Введем
матрицу наблюдаемости:
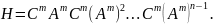 Эта
матрица состоит из транспонированной
матрицы
Эта
матрица состоит из транспонированной
матрицы
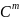 и ее произведений на матрицы
и ее произведений на матрицы
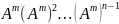 и имеет размерность (nxnp).
Тогда
критерием
полной наблюдаемости системы является
равенство ранга матрицы числу n.
и имеет размерность (nxnp).
Тогда
критерием
полной наблюдаемости системы является
равенство ранга матрицы числу n.12. Основные свойства систем управления для физических, производственных и социально-экономических объектов и процессов. Устойчивость и чувствительность.
Под устойчивостью понимается способность динамической системы возвращаться в равновесное состояние после окончания действия возмущения, нарушившего это равновесие. Неустойчивая система после воздействия возмущения удаляется от равновесного состояния или начинает совершать вокруг него колебания с нарастающей амплитудой. Устойчивость линейной системы определяется не характером возмущения, а структурой самой системы. Говорят, что система устойчива "в малом", если определен факт наличия устойчивости, но не определены ее границы. Система устойчива "в большом", когда определены границы устойчивости и то, что реальные отклонения не выходят за эти границы. Соответственно, и задача исследования систем на устойчивость может быть поставлена двояко: 1) устойчива ли система при заданном значении ее параметров; 2) в каких диапазонах можно изменять параметры системы, не нарушая ее устойчивости Если система описывается линейным дифференциальным уравнением, то ее устойчивость не зависит от величины возмущения. Линейная система, устойчивая при малых возмущениях, будет устойчива и при больших. Нелинейные системы могут быть устойчивы при малых возмущениях и неустойчивы при больших. Чувствительность – изменение статических и динамических характеристик под действием внешних условий, приводящих к изменению параметров звена или системы. Влияние среды на систему может привести к изменению операторов преобразования W(s), что приводит к возникновению систем с переменной структурой (нестационарные системы). Если изменение операторов преобразования во времени много медленнее собственных и вынужденных процессов, то говорят о квазистационарности (т.е. параметры системы изменяются очень медленно). Для систем управления важно, чтобы малые операторы вариации операторов не приводили к большим изменениям свойств системы в целом. Работоспособная система управления должна быть инвариантной к возмущениям и устойчивой. Количественно чувствительность применительно к динамическим процессам определяют функциями чувствительности, представляющие собой частные производные от координаты
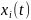 по исследованию параметру
по исследованию параметру
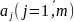 :
:
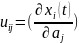
13. Оптимальное управление для физических, производственных и социально-экономических объектов и процессов. Критерии оптимизации.
Оптимальным называется управление, осуществляемое наилучшим по определенным показателям образом. Системы, реализующие оптимальное управление, называются оптимальными. Организация оптимального управления основана на выявлении и реализации предельных возможностей систем. При разработке систем оптимального управления одним из важнейших шагов является формулировка критерия оптимальности, под которым понимается основной показатель, определяющий задачу оптимизации. Именно по этому критерию оптимальная система должна функционировать наилучшим образом. В качестве критериев оптимальности выступают разнообразные технические и технико-экономические показатели, выражающие технико-экономическую выгоду или, наоборот, потери.- В первом случае оптимальное управление должно обеспечивать максимум критерия оптимальности, например производительности, коэффициента полезного действия, прибыли и т. д., при заданных реальных условиях работы и ограничениях. Во втором случае оптимальное управление должно обеспечивать минимум критерия оптимальности при заданных ограничениях, например расхода энергии, топлива, финансовых ресурсов и т. п. Критерий оптимальности обычно представляется в виде некоторого функционала. Функционал в таком случае можно определить как функцию, аргументы которой связаны с критериями оптимальности и сами являются функциями переменных. Обобщенный критерий качества работы динамической системы можно представить в виде функционала качества J = F(C,K,H,W,M,V), где С - стоимость разработки, создания и эксплуатации системы; К — качество функционирования; Н - надежность; W -потребляемая энергия; М - масса; V- объем. Критерии: 1) Критерий качества 2) Критерий минимального времени переходных процессов; 3) Критерий минимума отклонения переменных за время переходных процессов 4) Критерий минимума расхода 5) Критерий независимости выходных переменных от внешних возмущений или от других переменных 6) Критерий минимума отклонения показателя качества от его экстремального значения 7) Критерий минимума среднеквадратичной ошибки
14. Оптимальное управление для физических, производственных и социально-экономических объектов и процессов. Методы оптимизации.
Оптимальным называется управление, осуществляемое наилучшим по определенным показателям образом. Системы, реализующие оптимальное управление, называются оптимальными. Организация оптимального управления основана на выявлении и реализации предельных возможностей систем. Метод исследования функций классического анализа применяются в случае, когда аналитический вид критерия оптимальности известен, ограничения отсутствуют и возможно аналитическое или численное решение. Методы, основанные на использование неопределенных множителей Лагранжа, применяемые для решения задач оптимизации с ограничениями типа равенств. Методы вариационного исчисления используются для решения задач статической и динамической оптимизации, в которых критерий оптимальности представлен в виде функционала, а решение заключается в отыскании вида функций. Принцип максимума Потрягина применяется для решения задач оптимального управления объектами, описываемыми системами дифференциальных уравнений, причем на управление наложены ограничения, а решение отыскивается в виде разрывных функций. Метод динамического программирования является эффективным методом решения задач дискретных многостадийных процессов, для которых критерий оптимальности является аддитивной функцией критериев оптимальности отдельных стадий, ограничения на переменные учитываются при решении частных задач оптимизации на каждой стадии. Методы математического программирования включают в себя методы линейного и нелинейного программирования, причем методы линейного программирования используются для решения задач, в которых критерий оптимальности и ограничения сформулированы в виде линейных алгебраических уравнений.
15. Передаточная функция, типовые схемы и элементы систем управления для физических, производственных и социально-экономических объектов и процессов.
Преобразование дифференциальных уравнений по Лапласу дает возможность ввести удобное понятие передаточной функции, характеризующей динамические свойства системы. Передаточной функцией называется отношение изображения выходного воздействия Y(р) к изображению входного X(р) при нулевых начальных условиях:
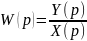 Передаточная
функция цепочки последовательно
соединенных звеньев.
В
этом случае имеем систему
уравнений:
Передаточная
функция цепочки последовательно
соединенных звеньев.
В
этом случае имеем систему
уравнений:
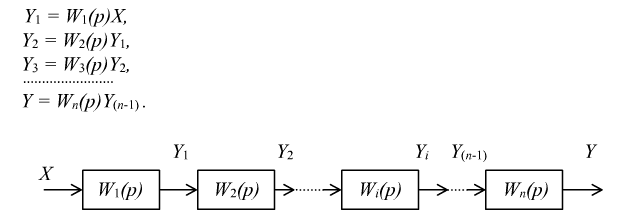 Исключив
отсюда промежуточные переменные,
получим:
Исключив
отсюда промежуточные переменные,
получим:
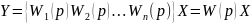
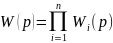 Параллельное
соединение звеньев направленного
действия.
При
параллельном соединении все звенья
имеют общий входной сигнал
Параллельное
соединение звеньев направленного
действия.
При
параллельном соединении все звенья
имеют общий входной сигнал 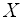 ,
а выходной сигнал
,
а выходной сигнал 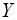 равен
сумме выходных сигналов отдельных
звеньев:
равен
сумме выходных сигналов отдельных
звеньев: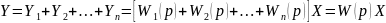 ,
где
,
где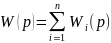
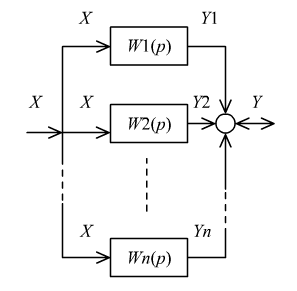
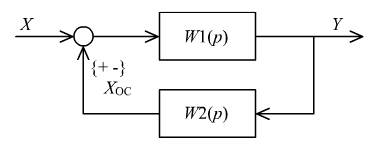
Звено, охваченное обратной связью. Обратная связь может быть положительной, если сигнал обратной связи
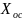 складывается с входным сигналом X,
или отрицательной, если вычитается
из X.
Охват
звеньев как положительной, так и
отрицательной обратными связями широко
применяется для коррекции статических
и динамических свойств замкнутых систем
автоматического управления с целью
придания заданных показателей качества
процесса управления.
Схема описывается
следующими уравнениями:
складывается с входным сигналом X,
или отрицательной, если вычитается
из X.
Охват
звеньев как положительной, так и
отрицательной обратными связями широко
применяется для коррекции статических
и динамических свойств замкнутых систем
автоматического управления с целью
придания заданных показателей качества
процесса управления.
Схема описывается
следующими уравнениями:
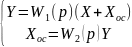 для положительной обратной связи
для положительной обратной связи
 для отрицательной обратной связи
для отрицательной обратной связи
16.Принципы регулирования и стабилизации для физических, производственных и социально-экономических объектов и процессов.
Различают следующие основные принципы управления:
Принцип разомкнутого управления – управляющее воздействие, вырабатывается только на основании задающего воздействия и априорной информации о возмущающих воздействиях, о значении управляемой величины, состоянии объекта управления, т.е. вектор управления, формируются только по вектору задания.
Достоинства: простота реализации.
Недостатки: возможность изменения У независимо от УЗ под воздействием возмущающих факторов или из-за изменения параметров системы.
Принцип применим при мало меняющихся внешних воздействиях, параметрах системы и не высоких требованиях к точности управления.
Управление по возмущению (принцип компенсации) – управляющее воздействие вырабатывается на основании информации о задающем и контролируемых возмущающих воздействиях, действующих на объект управления.
Достоинства: система инвариантна, т.е. независима по отношению к контролируемому (измеряемому) возмущающему воздействию. Система быстродействующая (принцип применим для управления инерционными объектами).
Недостатки: учитывается одно или ограниченное число возмущающих воздействий, на которые настроено компенсирующее устройство (регулятор по возмущению). Зависимость управляющего воздействия от возмущающего фактора может быть сложной и поэтому реализуется лишь приближенно.
Управление по отклонению (принцип обратной связи) – управляющее воздействие вырабатывается на основе информации об отклонении управляемой величины от заданной без учета причин вызвавших это отклонение.
Достоинства: система реагирует на сам факт, наличия отклонения ΔУ не зависимо от причин вызвавших это отклонение. Следствием этого достоинства является отсутствие жестких требований к стабильности характеристик элементов системы.
Недостатки: принцип не применим для инерционных объектов.
Часто управляющее воздействие вырабатывается не только в функции отклонения (ΔУ), но и в функции производных и интегралов этого отклонения.
Управление в функции отклонения называется регулированием, управляющее устройство (УУ) в этом случае называется регулятором, а вся система называется системой автоматического регулирования (САР).
Характерной особенностью данного принципа управления является наличие главной обратной связи необходимой для определения ΔУ.
Кроме главной обратной связи в системах могут быть местные обратные связи, которые служат для улучшения динамических характеристик систем.
17. ПИД-регулирование для физических, производственных и социально-экономических объектов и процессов.
Пропорционально-интегрально-дифференциальный (ПИД) (Эти три термина описывают простейшие элементы ПИД-контроллера. Каждый из этих элементов выполняет свою задачу и оказывает свое специфическое воздействие на функционирование системы.) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса.
ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи(сигнал рассогласования), второе — интеграл сигнала рассогласования, третье —производная сигнала рассогласования.
Пропорциональная составляющая
Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен заданному значению, то выходной равен нулю.
Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать.
Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления, при наличии задержек в системе, могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость.
Интегральная составляющая
Интегральная составляющая пропорциональна интегралу от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку.
Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечивать интегральная составляющая. Тем не менее, интегральная составляющая также может приводить к автоколебаниям.
Дифференциальная составляющая
Дифференциальная составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему.
