1.4 Енергія дислокацій
З модулем вектора Бюргерса безпосередньо пов'язана величина енергії дислокації Е. Оскільки вектором Бюргерса характеризується величина пружного перекручування (пружної деформації) кристалічної структури внаслідок утворення дислокації (деформована кристалічна структура працює як стисла або розтягнута пружина), то енергію дислокації можна оцінити як величину, що пропорційна квадрату деформації, тобто квадрату модуля вектора Бюргерса:
E~ ׀ b ׀ 2.
З модулем вектора Бюргерса також безпосередньо пов'язана величина мінімального зусилля, необхідного для переміщення дислокації в сусіднє положення й діючого на одиницю довжини дислокації:
FП = [ 2b/(1−μ)] {exp [−2π/(1−μ) (d/b)]},
де FП - сила Пайерлса; G - модуль пружності при зрушенні; μ - коефіцієнт Пуассона; d - відстань між сусідніми атомними площинами, у яких відбувається ковзання.
З формули Пайєрлса треба зробити важливий висновок про те, що найбільш легке ковзання здійснюється по площинах щільним упакування, тому що щільно упакованим атомним площинам відповідають максимальні міжплощинні відстані d.
Визначимо взаємне просторове розташування векторів dl і b. Вектор дислокації dl відповідно до рис. 1.5 розміщується перпендикулярно до площини риунка в напрямку [001]. Випливає, що цей вектор утворить із вектором Бюргерса b = a[010] прямий кут dl ┴ b, що служить характерною ознакою крайової дислокації.
Дислокацію оточують поля внутрішніх напружень: у верхній частині рис. 1.5 вище площини ковзання наявність екстраплощини свідчить про наявність напруг стиску, а нижче площини ковзання наявні напруги розтягання.
Із наявністю внутрішніх напружень навколо дислокації пов'язаний один із експериментальних методів виявлення дислокацій у кристалі. Для цього контрольовану поверхню кристала піддають хімічному травленню, у результаті якого розчиняється тонкий поверхневий шар кристала. Після травлення на поверхні кристала на місцях виходу дислокацій залишаються ямки травлення з гострою ямкою. В області дислокації кристал розчиняється інтенсивніше внаслідок наявності внутрішніх напружень (рис. 5.6). За кількістю таких ямок травлення, що припадають на одиницю площі поверхні кристала, визначають щільність дислокацій у кристалі, що служить одним із найважливіших контрольованих показників якості кристала.
Рисунок 5.6 - Схема виявлення дислокацій методом
травлення
Іншим методом контролю щільності дислокацій у кристалі служить пряме спостереження дислокаційних ліній у кристалі за допомогою інфрачервоного мікроскопа. Деякі кристали (наприклад, кристали напівпровідникових речовин) виявляються прозорими для інфрачервоних променів, які невидимі для неозброєного ока. Тому до звичайного металографічного мікроскопа додають спеціальною приставкою з електронно-оптичним перетворювачем і проводять безпосередній підрахунок ліній дислокацій, що потрапили в поле зору. Для об'єктивної оцінки щільності дислокацій у кристалі роблять усереднення показників (так само, як і для методу травлення) густини за декількома десятками полів зору.
Крім розглянутих крайових дислокацій, реальний кристал може також містити лінійні дефекти інших типів: гвинтові дислокації й дислокації змішаного типу. На рис. 5.7 наведені для порівняння схеми утворення крайо-вих (рис. 5.7 а, б) і гвинтових дислокацій (рис. 5.7 в). Якщо у випадку крайової дислокації її лінія дислокації (вектор dl) і вектор Бюргерса b були взаємно перпендикулярні, то у випадку гвинтової дислокації вектор дислокації dl і вектор Бюргерса b паралельні один одному: dl ׀׀ b. На рис. 5.7 в і вектор дислокації dl, і вектор Бюргерса b розміщуються паралельно напрямку [100]. Якщо крайова дислокація має характерну для неї площину ковзання, то гвинтова дислокація цього позбавлена.
У загальному випадку дислокації в кристалі можуть містити і крайову, і гвинтову компоненти й будуть тоді називатися дислокаціями змішаного типу. На рис. 1.8 показана замкнута петля лінії дислокації (як її видно в інфрачервоний мікроскоп типу МИК–1) з незмінним вектором Бюргерса b (нагадаємо, що вектор Бюгерса інваріантний, тобто зберігає ту саму величину й постійний напрямок уздовж всієї лінії дислокації).
На відміну від вектора Бюргерса b, вектор дислокації dl міняє свій напрямок від точки до точки при переміщенні уздовж лінії дислокації l. Крім чотирьох особливих точок дислокаційної петлі (а, b, с і d) дислокація на рис. 5.8 має обидві компоненти (і крайову, і гвинтову) і є дислокацією змішаного типу. Тільки в зазначених чотирьох точках дислокація має по одній компоненті: у точках а й з вектори
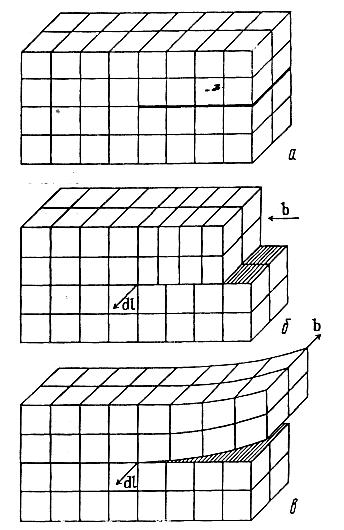
Рисунок 5.7 - Схеми виникнення дислокацій у кристалічній структурі: а - вихідна структура; б - крайова дислокація; в - гвинтова дислокація
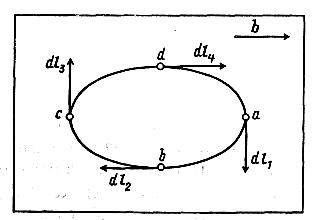
Рисунок 5.8 - До визначення дислокацій: крайового,