1.4 Координаційні числа й координаційні

багатогранники

Число атомів (іонів протилежного знака), складове найближче оточення даного атома (іона), називається його координаційним числом, а геометрична фігура, що виходить при сполученні центрів цих атомів (іонів) прямими лініями, - його координаційним «багато-гранником».

У структурі міді Сu (рисунок 1.10) кожний атом міді оточений дванадцятьма найближчими до нього такими ж атомами, розміщеними по вершинах кубооктаедра. Наприклад, до координаційного багато-гранника атома 1 належать атоми 2, 2, 2 і інші, не зображені на рисунку атоми, що віддалені від нього на відстані, що дорівнює половині гранної діагоналі осередку . Таким чином, координаційне число атома міді в її структурі дорівнює 12, координаційний багатогранник - кубооктаедр.

У структурі повареної солі NaCl (рисунок 1.10.) навколо кожного іона натрію розміщуються по октаедру шість найближчих іонів хлору, і навпаки, навколо кожного іона хлору розміщуються по октаедру шість найближчих іонів натрію. Отже, координаційне число натрію в структурі NaCl дорівнює 6, координаційний багатогранник - октаедр; координаційне число хлору в тій самій структурі дорівнює 6, координаційний багатогранник - октаедр.

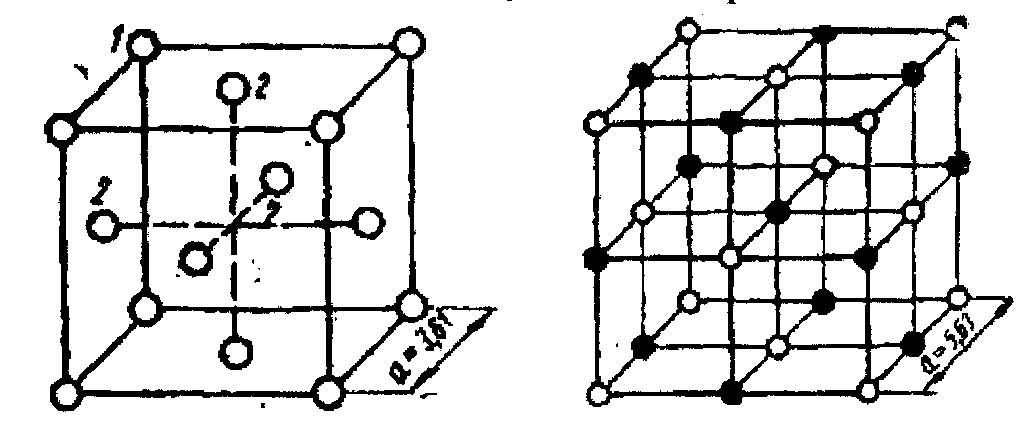
Рисунок 1.10 - Схеми структур міді(а) та повареної солі (б) для визначення координаційного числа (КЧ) та координаційного багатогранника

У випадку іонних решіток у структурі поєднуються іони різних радіусів, тому координаційне число (тобто число атомів, що групуються навколо кожного катіона або число катіонів, що оточують аніон) буде залежати від відношення радіуса катіона R_к до радіуса аніона R_a, тобто від величини R_к : R_а.

Координаційні числа зумовлюють різне розміщення аніонів і катіонів і, отже, дозволяють визначити характерні особливості структур тієї або іншої хімічної сполуки.

Якщо координаційне число дорівнює 2, що може бути при відношенні

R_к : R_a ≤ 0.15 ≤ 0.22, то два аніони будуть перебувати на рівній відстані від катіона й утворювати фігуру у вигляді гантелі.

Аналогічно для інших (див. таблицю 1.2).

Таблиця 1.2-Відношення радіусів залежно від КЧ

Координаційне число	Форма координаційного поліедра	Відношення радіусів
2 3 4 6 8 12	Гантель Трикутник Тетраедр Октаедр Куб Кубооктаедр	від 0 до 0.15 від 0.15 до 0.22 від 0.22 до 0.41 від 0.41 до 0.73 від 0.73 до 1.37 1

1.5 Визначення стехіометричної формули речовини

У кристалічній структурі положення частинок речовини збігається з вузлами решітки або частинки розміщуються навколо вузлів симетричними групами. Визначення хімічної (стехіометричної) формули речовини грунтується на підрахунку числа атомів кожного сорту, що припадають на один елементарний осередок.

Число структурних одиниць показує, скільки треба взяти атомів (молекул) даної хімічної сполуки, щоб побудувати один елементарний осередок. Так, для кристала типу АВ, наприклад NaCl (див. рисунок 1.11 а), на один осередок припадає по чотири атоми А і В. Отже, число структурних одиниць Z=4.

Число Z завжди більше одиниці й набуває лише цілих чисельних значень.

Приклади визначення стехіометричної формули речовини:

У структурі CsCl (рисунок 1.11 б) один атом Сl перебуває в центрі осередку, атоми Cs займають 8 вершин, тобто на 1 осередок припадає 8x1/8=1 атом Cs, отже, А : В= 1:1, стехіометрична формула АВ (CsCl), Z=2.

Рисунок 1.11 - Схеми структур CsCl(a) та Ca₂F для визначення стехіометричних формул

У структурі флюориту Ca₂F (рисунок 1.11) атоми Са займають вузли гранецентрованого осередку, число структурних одиниць типу А (Са) дорівнює 4. У найпростіших структурах для підтвердження хімічної формули сполуки можна використовувати координаційні числа. Так, у структурі хлористого натрію (КЧ Na_Cl=6) відношення координаційних чисел 6:6=1:1, що приводить до стехіометричної формули АВ (NaCl).

У структурі флюориту КЧ Са=8, КЧ F_Ca=4, відношення координаційних чисел дорівнює 8:4= =2:1, стехіометрична формула АВ₂ (Ca₂F).

За КЧ зручно класифікувати структури бінарних сполук (АВ, АВ₂ і т.д.).