4.11 Антисиметрія

Перетворення антисиметрії вводяться для об'єктів, що мають властивість змінювати знак. Прикладом може бути позитивний або негативний електричний заряд.

Операції антисиметрії перетворять об'єкт у симетрично еквівалентне положення та одночасно змінять його знак.

Як зазначив Шубніков, такі фізично реальні об'єкти, як електрон і позитрон, провідник у діелектрику й діелектрик у провіднику, крапелька води в повітрі й пухирець повітря у воді, фотографічні негатив і позитив, форми росту й форми розчинення кристалів, вимагають введення в навчання про симетрії поняття протилежно рівних або антирівних фігур. Антирівними вважаються фігури геометрично рівні, але які мають різний знак.

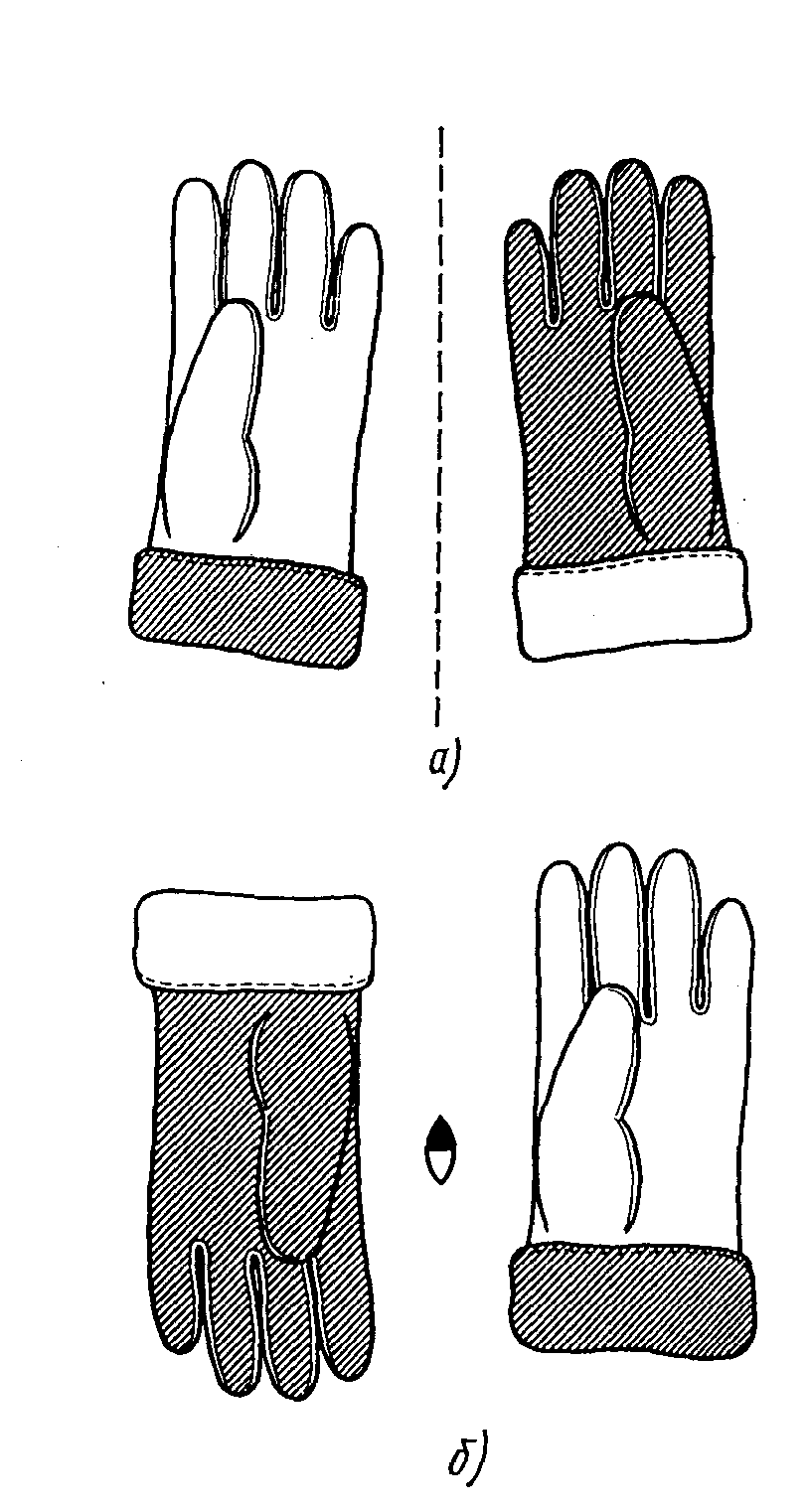
Щоб скласти зрозуміле уявлення про антирівність фігур, наведемо приклад А. В. Шубнікова: візьмемо рукавички, виготовлені зі шкіри, пофарбованої з лицьової сторони в чорний, а з виворотного боку в білий колір (рисунок 4.16).

Рисунок 4.16 - Антирівні фігури за Шубніковим

Рукавичка може бути: 1) правою білою із чорним одворотом, 2) лівою білою із чорним одворотом, 3) правою чорною з білим одворотом, 4) лівою чорною з білим одворотом.

Праву рукавичку при бажанні можна вивернути на виворіт і надягти на ліву руку. У цьому розумінні кожна рукавичка є чорною й білою, правою й лівою. При цьому:

дві праві білі рукавички рівні;

права біла й права чорна антирівні;

права й ліва білі енантіоморфні;

права біла й ліва чорна антиенантіоморфні.

Нагадаємо, що перетворення у звичайній площині симетрії зв'язують між собою дзеркально рівні фігури, не повертаючи їх «з особи навиворіт». Перетворення ж у площині антисиметрії не тільки переводить білу рукавичку в дзеркально рівне положення, але й робить її чорною (рисунок 4.17 а).

Рисунок 4.17 – Перетворення площиною антисиметрії (а) і віссю антисиметрії другого порядку (б)

На рисунку 4.17 б показано перетворення анти-симетричною віссю («антивіссю») другого порядку, перпендикулярною до площини креслення: чорна рукавичка повертається на 180° у площині креслення й одночасно перетвориться в білу.

Чорний і білий кольори тут символізують зміну знаку властивості, наприклад знаку електричного заряду, знаку спіна електрона.

Сполучаючи праву білу рукавичку із правою чорною, одержимо праву рукавичку, що не має кольору, тобто «сіру». Класичне навчання про симетрію мало справу саме з «сірими» фігурами. На рисунку 4.18 порівняні деякі перетворення симетрії й антисиметрії.

Рисунок 4.18 - Симетричні (а) і антисиметричні

(б) перетворення

Групи симетрії, у які входять операції антисиметрії,називають «чорно-білими» групами. Для кінцевих кристалографічних фігур існує 58 точкових чорно-білих груп. Введення антисиметричної трансляції збільшує число осередків Браве на площині від п'яти до десяти, а в просторі замість 14 «сірих» осередків Браве виходить 36 тривимірних «чорно-білих» осередків Браве.

Нескінченні перетворення описуються чорно-білими, або так званими шубніковськими групами, їх є 1651. В їх число входять й 230 відомих нам просторових груп.

Поняття антисиметрії відіграє істотну роль при визначенні структури кристалів і симетрії елементарних частинок.