4.10 Зворотні гратки

У рентгеноструктурному аналізі кристалів і фізиці твердого тіла зручно мати справу з так званими зворотними ґратками, що будуються в такий спосіб:

1) якщо звичайні прямі ґратки побудовані на векторах трансляцій а, b , с, то осі зворотної до неї ґратки а*, b *,с* визначаються як векторні добутки

а*=[b×c], b*=[c×a], c*=[a×b]; (1)

2 ) осьові параметри зворотних ґраток а*, b *, с* дорівнюють зворотним величинам міжплощинних відстаней плоских сіток прямих ґраток, перпендикулярних до цієї осі. Кожній площині (hkl) прямої решітки відпо-відає у зворотних ґратках вузол [[hkl]]*. Нескінчен-ній родині паралельних площин {hkl} у просторі прямих ґраток відповідає у просторі зворотних ґраток нескінченна родина точок [[hkl]]* уздовж напрямку, нормального до цих пло-щин. Відстані цих точок від точки, взятої за початок координат у зворотному просторі, дорівнюють 1/d, 2/d, 3/d,…, де d=d_hkl— відстань між площинами {hkl} у прямій ґратці (рисунок 4.12).

Рисунок 4.12 - Пряма (а) і

зворотна (б) ґратки

Зоні площин прямих ґраток відповідає сітка із точок (вузлів) зворотних ґраток, причому вісь зони прямих ґраток нормальна до площини сітки зворотних ґраток. Нарешті, прямим просторовим ґраткам із площин {hkl} відповідають зворотні тривимірні ґратки із точок [[hkl]]*.

Основні вектори а*, b *, с * зворотних ґраток визначаються векторними добутками (1) або скалярними добутками:

(a*·a)=(b*·b)=(c*·c)=1, (2)

(a*·b)=(a*·c)=(b*·c)=(b*·a)=(c*·b)=(c*·a)=0.

З рівності (1) видно, що вектор а* нормальний до площини векторів b і с і т. п. Трійка векторів а*, b *, с* вибирається так, щоб вони, як і вектори а, b, с, становили праву трійку.

Вектори а*, b*, с* являють собою площинки елементарних паралелограмів у координатних площинах прямих ґраток, а за абсолютною величиною вони обернено пропорційні міжплощинним відстаням прямих ґраток:

|а*|= , ,

(у знаменнику - мішаний добуток векторів).

Прямі й зворотні ґратки сполучені взаємно, тобто ґратки, побудовані на осях а, b, с, є зворотними стосовно ґраток а*, b *, с*, а ґратки, побудовані на векторах а*, b*, с*,-зворотними стосовно ґраток а, b, с.

Наведемо основні властивості зворотних ґраток.

1 Вектор

(3)

зворотних ґраток перпендикулярний до площини (hkl) прямої ґратки, а довжина цього вектора дорівнює зворотній величині відстані d між площинами {hkl} прямої ґратки, тобто

, (4) 2 Об’єм V* елементарного осередку зворотних ґраток дорівнює зворотній величині об’єму V елементарного осередку прямих ґраток (і навпаки):

V* = (а* [b* ×с*])=1/V, (5)

V=(a·[b×c])=1/V*.

Для доведення першої властивості помітимо, що площина АВС із індексами (hkl) за визначенням, відтинає на координатних осях прямих ґраток відрізки а/h,b/k,c/l (рисунок 4.13).

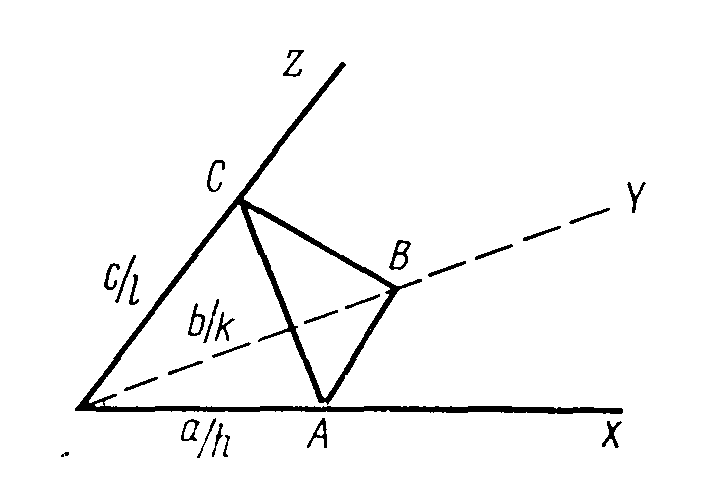
Рисунок 4.13- До пояснення властивостей зворотних ґраток

Отже, вектор ( ), тобто відрізок АB на рисунку 4.13 лежить у площині (hkl). Цей вектор перпендикулярний до того, що їхній скалярний добуток дорівнює нулю:

. (6а)

Точно так само вектор H^*_hkl перпендикулярний до вектора ( ), тобто до відрізка СА на рисунку 4.13

. (6б)

Якщо вектор H^*_hkl зворотних ґраток нормальний до двох непаралельних напрямків у площині (hkl), то він нормальний до самої площини (hkl). Якщо n— одиничний вектор нормалі до площини (hkl), то (а·n/h)— міжплощинна відстань для родини паралельних площин {hkl}.Оскільки n = Н*/|H*|, а також враховуючи рівність (2), отримаємо :

(7)

Перша властивість доведена.

Друга властивість безпосередньо складається із визначень і формул (1) і (3). Таким чином,

(8)

Кожній площині (hkl) прямої решітки відповідає вузол [[hkl]]* зворотних ґраток. Оскільки прямі й зворотні ґратки сполучені взаємно, така ж відповідність є між вузлами прямих ґраток і площинами зворотних ґраток.

Покажемо, наприклад, що оберненою до гранецентрованої ґратки буде об’ємно - центрована ґратка. Справді, у гранецентрованих кубічних ґратках відстані між площинами {100}, {010}або {001} дорівнюють а/2. Отже, у зворотних ґратках уздовж осей Х, В, Z є точки, розміщені на відстанях = . Їхні символи [[ 00]]; [[0 0]]; [[00 ]]. Відстані між площинами {111} у прямих ґратках дорівнюють , отже, у зворотних ґратках цим площинам відповідає точка на прямій <111>^* на відстані від початку координат; якщо початок координат збігається з вершиною куба, то точка [[ ]] знаходиться в центрі куба. Ті самі співвідношення для ромбічних осередків показані на рисунку 4.14

Рисунок 4.14 - Пряма гранецентрована (а) і зворотна до неї об’ємно - центрована (б) ґратки

Аналогічно можна показати, що кубічній об’ємно - центрованій ґратці відповідає обернена гранецентрована.

Міллерівські індекси системи паралельних площин прямих ґраток є координатами ряду зворотних ґраток.

З формул (1), (2), (3) неважко вивести співвідношення між параметрами прямого осередку а, b, с, α, β, γ, і зворотного осередку а*, b* ,с* , α*, β *, γ *:

(9)

звідки

(9а)

і

(10)

Поняття про зворотні ґратки вводиться в основному для опису періодичного розподілу відбиваючої здатності кристала стосовно рентгенівських променів. Відбиття рентгенівських променів від площин структури кристала описується формулою Вульфа — Брегга.

,

де λ - довжина хвилі рентгенівського випромінювання;

d - міжплощинна відстань для родини паралельних відбиваючих площин; n - ціле число, що характеризує порядок дифракційного спектра.

З умови Вульфа - Брегга видно, що при постійній λ великому d відповідає малий кут θ, тобто чим більше міжплощинна відстань, тим ближче напрямок відбитих променів до напрямку падаючого пучка. Відбиття рентгенівських променів від нескінченно протяжних ідеальних кристалів повинні бути точковими.

Кожен вузол зворотних ґраток відповідає можливому відбиттю від площин прямих ґраток кристала. Напрямок вектора зворотних ґраток H^*_hkl збігається з напрямком відбиття від площин {h k l}, а n-й вузол зворотних ґраток у цьому ряді відповідає відбиттю n-го порядку від цих площин.