4.5 Інверсійні осі симетрії (Li)

Інверсійною віссю симетрії називається пряма, при повороті навколо якої на 360° з відповідним перенесенням - відбиттям (інверсією) через центр кристала аналогічні частини сполучаються самі із собою ”n” ціле число раз. У кристалах можуть бути наявними інверсійні осі четвертого L_i4 і шостого L_i6 порядків, інші осі відповідають раніше розглянутим елементам симетрії: L_i1=С; L_i2=Р; L_i3 - відповідає осі симетрії третього порядку (L₃) за наявності центра інверсії.

Для визначення інверсійних осей симетрії кристал рекомендується орієнтувати так, щоб L_i4 або L_i6 розміщалася вертикально. У подальшому при такій орієнтації кристал повертається на 60° або на 90°, а елементи кристала (вершини, ребра, грані) переносяться через його центр на протилежні сторони. Якщо після повороту навколо заданої осі зазначені елементи огранювання (вершина, ребро, грань) верхньої частини кристала будуть являти собою відбиття-інверсію через центр нижньої частини, то дана вісь дійсно є віссю інверсії певного порядку (L_i4 або L_i6), якщо ж немає - інверсійна вісь відсутня. Порядок осі визначається сумою частин кристала, які повторюються при його повороті на 360°.

Р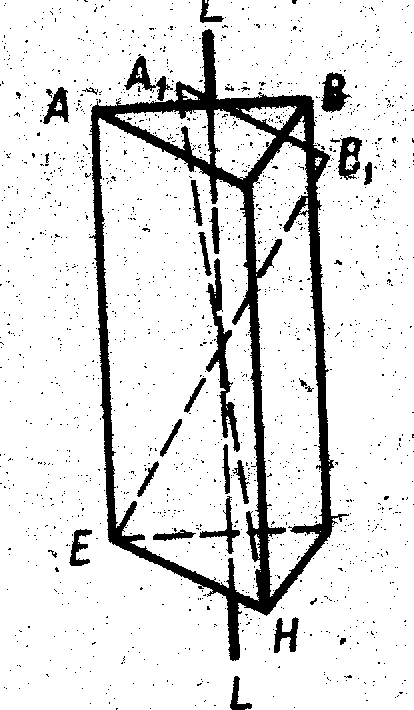 озглянемо інверсійну вісь у багатограннику, зображеному на рисунку 4.6. Він має вісь третього порядку L₃ (пряма LL), що одночасно є інверсійною віссю симетрії шостого порядку (L_i6). При повороті всіх частин багатогранника навколо осі LL на 60° і подальшому відбитті їх у центральній точці фігура сполучиться сама із собою. Так, після повороту ребра АВ навколо LL на 60° воно займе положення А₁В₁, що

Рисунок 4.7 - Приклад багатогранника

з інверсійною віссю третього порядку

шляхом відбиття через центр сполучить А₁В₁ з ребром НЕ.

При повному повороті на 360° таких сполучень буде шість. Отже, вісь LL є інверсійною віссю шостого порядку. Д

Рисунок 5.6.

ля прикладу визначимо елементи симетрії куба (рисунок 4.7). У кубі можна встановити центр інверсії С, 3 осі четвертого порядку – 3L₄, що проходять через середини граней; 4 осі третього порядку 4L₃, що проходять через вершини куба; 6 осей другого порядку - 6L₂, що проходять через середини ребер і 9 площин симетрії. Всі вони можуть бути виражені формулою 3L₄4L₃6L₂9РС.

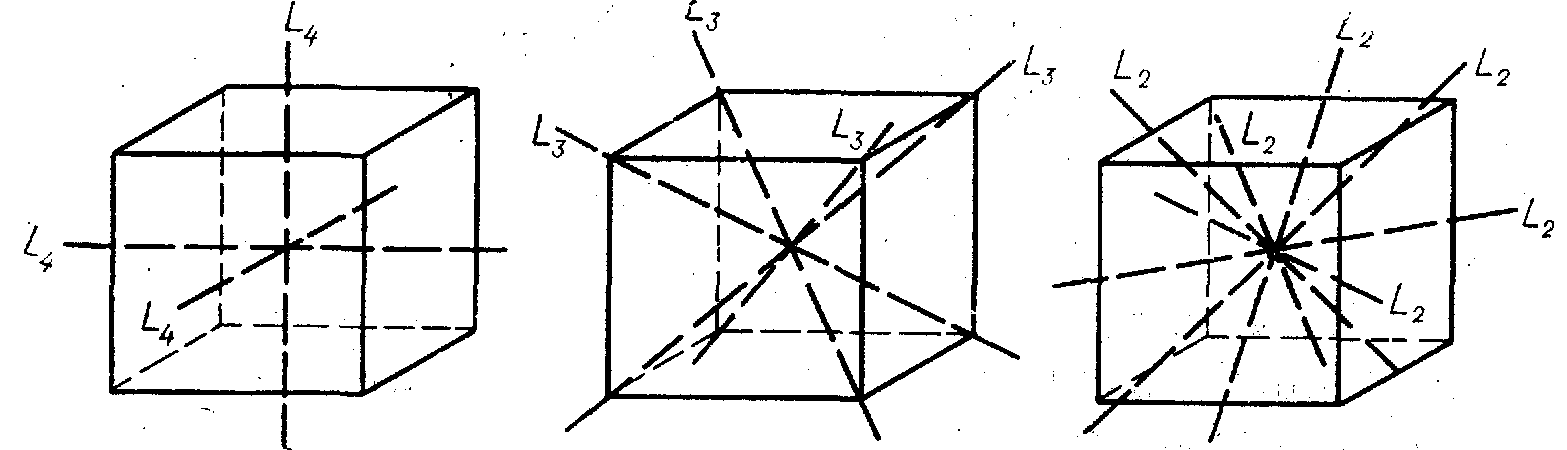
Рисунок 4.7 - Можливі елементи симетрії куба

4.6 Принцип Кюрі

На рисунку 4.8 показані плоскі сітки паркету або мозаїки, складені з однакових багатокутників. Видно, що осередки з осями симетрії 2, 8, 4, 6 заповнює площина симетрично й безупинно. Але безупинно заповнити площину п'яти- або семикутниками не вдається - залишаються дірки.

На візерунку паркету такі дірки заповнюються іншими фігурками, що порушують симетрію, але в системі матеріальних частинок наявність таких «дірок» створювала б можливість переміщення частинок, тобто нестійкість структури.

Може здатися, що восьмикутники все-таки заповнюють площину, тобто що вісь 8 (L₈) у безперервному візерунку можлива. Насправді дірки між восьмикутниками (рисунок 4.8) довелося заповнити квадратиками, а в результаті змінилася симетрія: як не дивно, але в цьому візерунку симетричного осі 8 восьмикутника немає; є тільки вісь 4, тому що восьмикутник симетрично оточено лише чотирма квадратиками. Розглядаючи симетрію фігури, потрібно чітко розрізняти, чи говоримо ми про симетрію тільки самої фігури або ж про симетрію фігури і її оточення. В окремо взятого восьмикутника, звичайно, є симетрії 8 (L₈), але в оточенні інших восьмикутників його симетрія понизилася до осі 4 (L₄), що видно з чотирьох квадратиків.

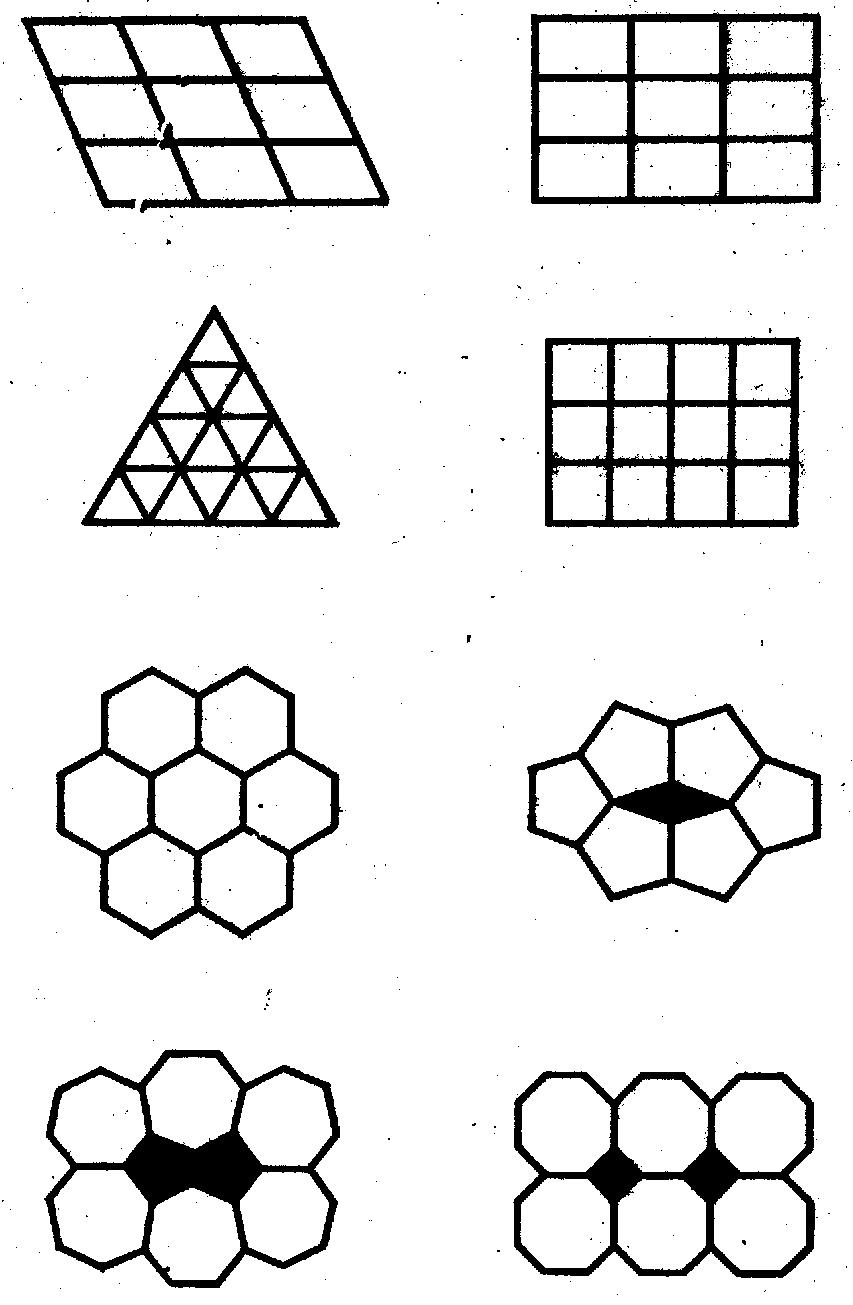
Рисунок 4.8 - Плоскі сітки складені з багатогранників з осями симетрії 8-го порядку

Раніше говорилося, що в куба є три осі 4 (3L₄), чотири осі 3 (4L₃), шість осей 2 (6L₂). Вісь 4 виходить у центрі грані куба, там само перетинаються чотири площини симетрії 4m(L₄4Р).

Нарисуємо на такій грані рівносторонній трикутник.

У

Рисунок 4.10 - До ілюстрації

принципу Кюрі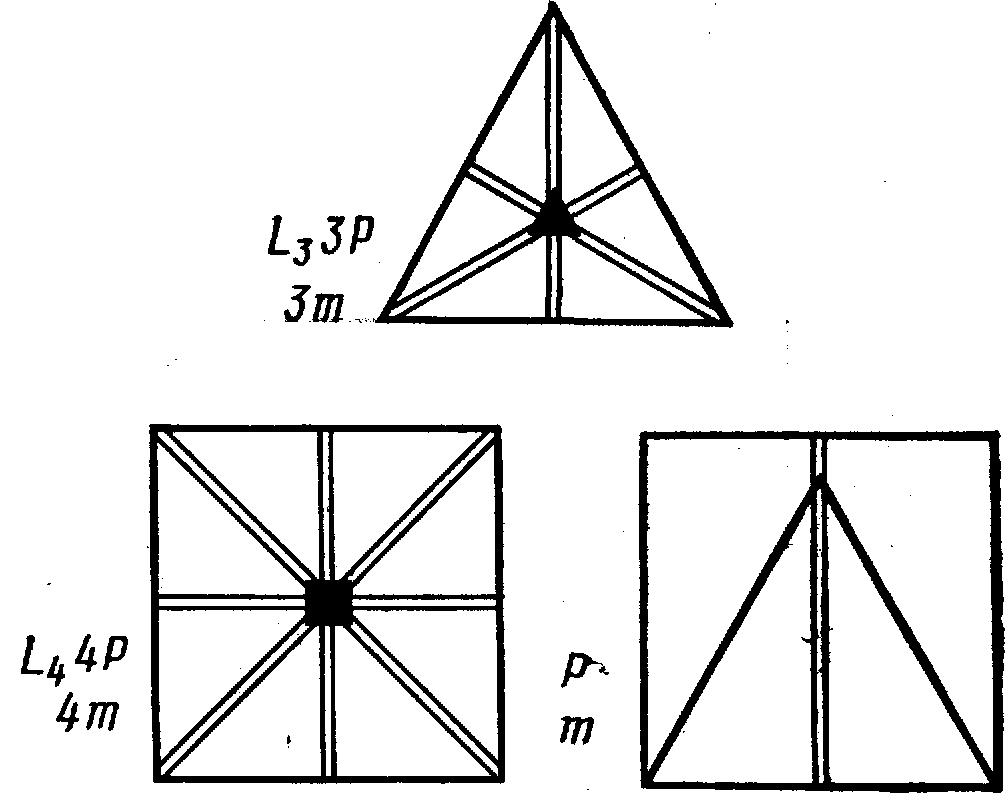

самого багатокут-ника є вісь 3 (L₃) і вздовж її три площини симетрії 3m(L₃3Р₁). Але якщо трикутник перебуває на грані куба, то квадрат і трикутник «втрачають» осі симетрії й частину площин, а «виживає» тільки одна загальна площина симетрії (рисунок 4.9).

Це окремі випадки принципу Кюрі: якщо накладаються одне на одне два явища або явище й навколишнє його середовище, то зберігається лише та симетрія, що є загальною для обох.