3.5 Сітка Вульфа

Для вирішення кількісних завдань за допомогою стереографічної і гномостереографічної проекцій користуються звичайно градусними сітками.

Найбільш часто застосовувана сітка Вульфа.

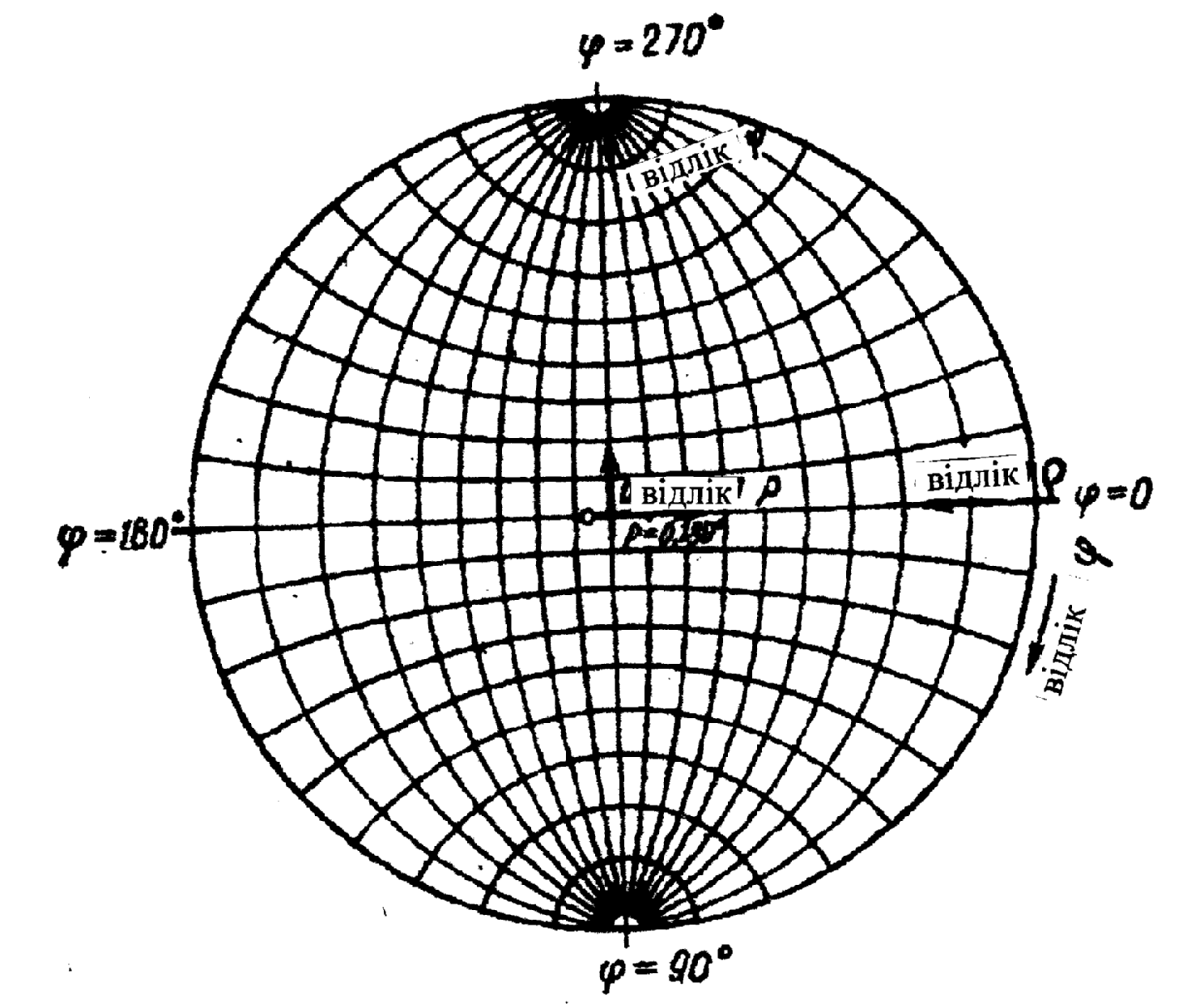
Рисунок 3.10 - Схема сітки Вульфа та відліку кутів за нею

Сітка Вульфа (рисунок 3.10) - це стереографічна проекція всієї системи меридіан і паралелей, нанесених на поверхню сфери. Площиною проекцій є площина одного з меридіанів. Положення будь-якої точки на сітці Вульфа визначається її сферичними координатами φ і ρ.

Сітка Вульфа стандартно креслиться на колі діаметром 20 см, лінії паралелей і меридіанів проводять через 2°. Відстані між ними можна розділити на око ще на 4 частини, тобто працювати з точністю до 0.5°.

Розділ 4 Симетрія кристалів

4.1 Загальні поняття про симетрію кристалів

Симетрією називається властивість геометричних фігур повторювати свої аналогічні частини деяке ціле число разів.

Симетрія геометричних тіл має два поняття: геометричне й фізичне. Якщо з геометричної точки зору до симетричних тіл відносять тіла, які складаються з однакових за зовнішньою формою й розміром частин, то фізична симетрія передбачає не тільки геометричну рівнозначність, але й фізичну - колір, твердість та ін.

Елементами симетрії називають допоміжні геометричні образи (точки, прямі, площини), за допомогою яких виявляється симетрія фігури або багатогранника.

Елементи симетрії кристалів

- центр інверсії C;

- поворотні осі симетрії L;

- інверсійні осі симетрії L_i;

- площини симетрії P;

- одиничні напрямки OH.

4.2 Центр інверсії (c)

Центром інверсії називається така точка всередині фігури, через яку, якщо провести пряму, то з обох сторін від неї на однакових відстанях перебувають аналогічні частини фігури. Як видно з рисунка 4.1, проведені прямі АА₁, ВВ₁ і ДД₁ на однакових відстанях від точки С з обох сторін мають аналогічні частини трикутників АВС і А₁В₁С₁. При цьому верхній трикутник АВС повернутий відносно нижнього трикутника А₁В₁С₁ на 180°. Це явище й одержало назву інверсії, а сама точка С, через яку проходить відбиття трикутника АВС у трикутник А₁В₁С₁,- центра інверсії. На рисунку 4.1 б зображені два паралелограми, грані яких також пов'язані між собою центром і нверсії.

Н

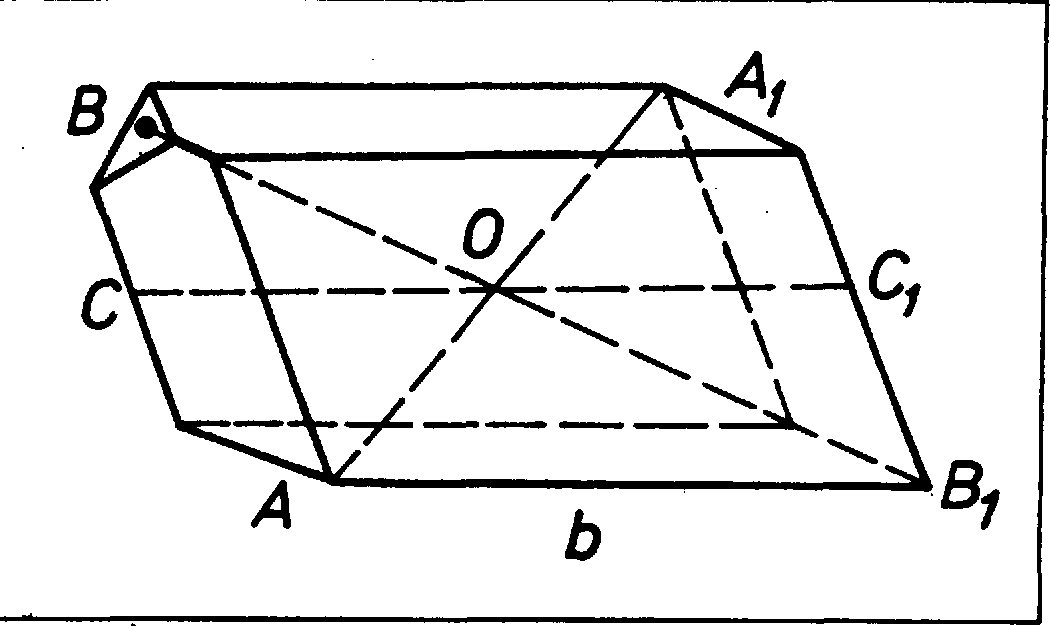
Рисунок 1.

Рисунок 4.1 - Два трикутники (а) та два паралелограми (б) пов’язані між собою центром інверсії

аявність центра інверсії в об'ємній моделі зображена на рисунку 4.1. Як видно, будь-яка пряма, проведена через центр цього багатогранника з обох сторін від точки С на однакових відстанях, перетинає аналогічні частини фігури, тобто якщо з однієї сторони точки С розміщена вершина А, відповідно із другої сторони на тій самій відстані розмішена аналогічна вершина А₁. Це стосується будь-яких точок, які можна розмістити як на ребрах, так і на гранях кристала.

Н

Рисунок 3.

а відміну від рисунка 4.1 а, у якому центр інверсії наявний, у багатограннику, зображеному на рисунку 4.1 б, центр інверсії відсутній. Це пов'язане з тим, що хоч прямі АА₁ і СС₁ з обох сторін від точки О мають однакові частини фігури (вершина - вершина, ребро - ребро), пряма ВВ₁ з обох сторін від точки О перетинає різні частини фігури: ОВ – грань, ОВ₁ – вершину. Таким чином, необхідною умовою наявності центра інверсії в кристалах є наявність попарно-паралельних граней. Якщо в кристалі наявна хоча б одна грань, що не має собі паралельної, то центр інверсії відсутній.

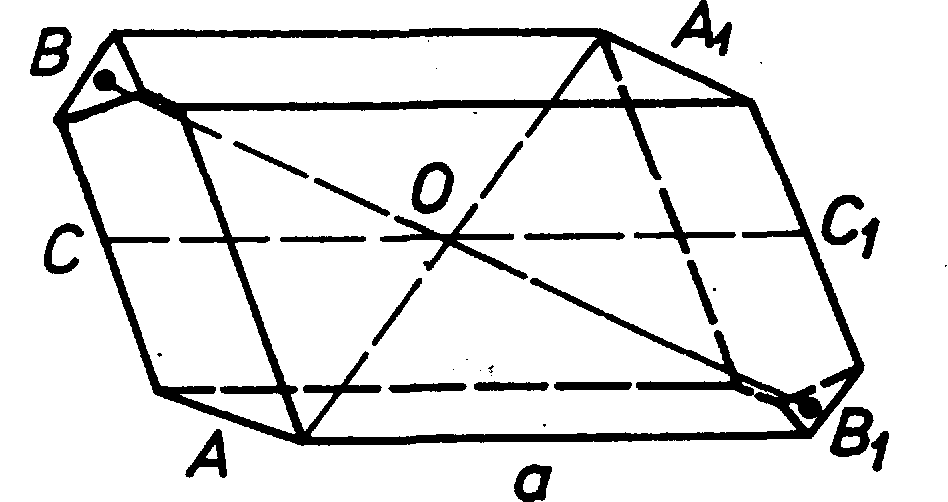
Н а моделях кристалів центр інверсії можна визначити в такий спосіб. Покладемо модель будь-якою гранню на стіл. Якщо у всіх випадках угорі виявляється грань, паралельна і рівна першій, то центр інверсії є, якщо ж вгорі виявиться ребро або вершина, або грань, паралельна, але не рівна першій, то центра інверсії в кристалі не існує (рисунок 4.2).

Рисунок 4.2 - Ілюстрація до пояснення наявності (а) і відсутності (б) центра інверсії в об'ємних моделях кристалів