Розділ 3 Кристалографічні проекції

3.1 Сферична проекція

В

Рисунок 3.1 - Нормалі кристалографічного багатогранника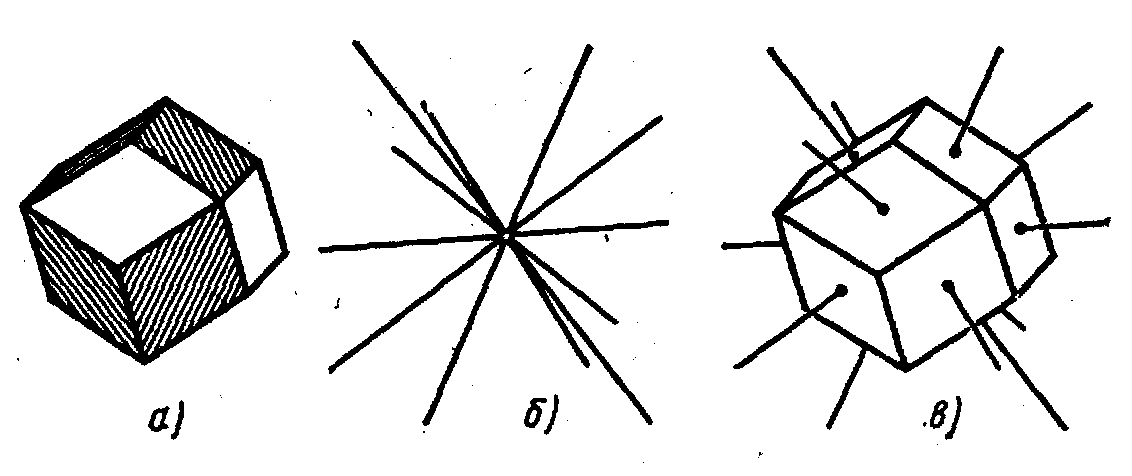

ізьмемо кристал. Прове-демо прямі перпендикулярно до граней кристала (рисунок 3.1). Із точки перетину прямих опише-мо сферу (рисунок 3.2 а). Перетин нормалей граней кристала з поверхнею сфери являє собою сферичну проекцію цих нормалей (рисунок 3.2 б). Кожна нормаль (як і будь-який інший напрямок) проектується на поверхню сфери проекцій у вигляді точки. На рисунку 3.2 подана окремо повна сферична проекція кристала, кожній із точок проекції відповідає одна із граней кристала.

Сферичну проекцію можна будувати без заміни граней кристала їхніми нормалями. У цьому випадку всі грані кристала шляхом паралельного перенесення переміщають у центр сфери проекцій (одержують так званий кристалічний комплекс) і будують відбитки перетину цих граней зі сферою проекцій.

Положення будь-якої точки на поверхні сфери проекцій можна охарактеризувати двома сферичними координатами:  - полярна відстань, відлічувана за будь-яким напрямком від нуля (північний полюс) до 180° (південний полюс);  - довгота, відлічувана по екватору від меридіана, взятого за нульовий меридіан (рис. 3.3).

С ферична проекція кристала наочна, але для практичного засто-сування її треба спро-

ктувати на площину й користуватися стерео-графічними, гномо-стереографічним й гно-монічними проекція-ми.

Рисунок 3.2 - Побудова сфери проекції(а) та сферичної проекції (б);сферична проекція додекаедра(в)

Рисунок 3.3 - Сферичні координати на поверхні сфери проекцій

3.2 Стереографічна проекція

За площину стереографічної проекції Q вибирається екваторіальна площина, на яку сфера проектується у вигляді кола проекцій (рисунок 3.4). В одному з полюсів цієї сфери міститься точка зору («очна точка») S.

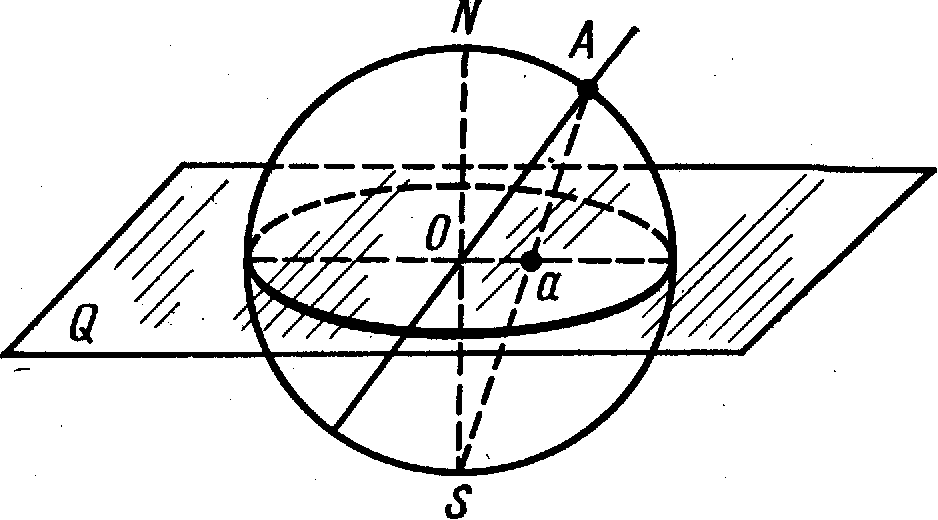
Рисунок 3.4 - Принцип побудови стереографічної проекції

Щоб спроектувати пряму, наприклад ОA, проводимо лінію AS від полюсної точки А на сфері проекцій до точки зору S. Точка а є перетином лінії AS із стереографічною проекцією напрямку ОА.

Стереографічні проекції напрямків зображуються точками всередині кола проекцій (рисунок 3.5).

Рисунок 3.5 - Стереографічні проекції площин розміщених відносно площини проекції : a - перпендикулярно; б - у самій площині; в - під косим кутом до неї

Очевидно, вертикальний напрямок проектується як точка в центрі кола проекцій, горизонтальний - як дві точки на екваторі. Площина, що проходить через точку O і перетинає сферу, проектується на стереографічну проекцію у вигляді відповідної дуги великого кола.

Щоб не завантажувати креслення, проектують тільки перетин площини з верхньою півсферою, а нижню частину площини звичайно не проектують.

Рисунок 3.6 - Стереографічні проекції напрямків, розміщених відносно площини проекцій: а- перпендикулярно; б- у самій площині; в- під косим кутом до неї

Стереографічні проекції горизонтальних площин (рисунок 3.6) являють собою коло, що збігається із границями кола проекцій; проекції вертикальних площин збігаються з діаметрами кола проекцій, а проекції похилих площин зображуються дугами, що опираються на кінці діаметра кола проекцій.

Для побудови стереографічної проекції особливо важливі дві її властивості:

1) будь-яке коло, проведене на сфері, зображується на стереографічній проекції також колом (в окремому випадку прямою лінією);

2) на цій проекції не спотворюються кутові співвідношення: кут між полюсами граней на сфері, вимірюваний по дугах більших кутів, дорівнює куту між стереографічними проекціями тих самих дуг.

Стереографічні проекції використовуються головним чином для відображення симетрії кристала.