
- •1.Единственность решения задачи Коши Теорема:
- •2.Непрерывная зависимость решения
- •3.Существование производной по параметру для решения з. Коши
- •4.∃ И ед. Решения з. Коши n-го п-ка на отр.
- •6. Ед. Решения з. Коши норм. Системы
- •7.Устойчивость по первому приближению
- •8. Определение непр. Зависимости решения з.Коши от начального усл.
- •29. Сформулировать и доказать теорему о существовании общего интеграла у дифференциального уравнения в полных дифференциалах.
- •32.Опишите процедуру исследования решения системы обыкновенных дифференциальных уравнений на устойчивость по первому приближению.
- •43.Дать определение асимптотической устойчивости решения нормальной системы дифференциальных уравнений.
- •47.Дать определение устойчивости по Ляпунову для нулевого решения нормальной системы дифференциальных уравнений.
- •49.Дать определение общего интеграла и общего решения обыкновенного дифференциального уравнения 1-го порядка.
- •51.Сформулировать и доказать теорему об устойчивости по Ляпунову для линейной системы дифференциальных уравнений с постоянными коэффициентами.
- •58.Какие условия должны быть выполнены, чтобы задача Коши была корректной по Адамару?
4.∃ И ед. Решения з. Коши n-го п-ка на отр.
Теорема
Задача Коши
 ⦁
⦁
для
уравнения n-го п-ка,
разрешённого отн. старшей пр., правая
часть которого
 удовл. условиям:
удовл. условиям:
1) непр по всем аргументам
2)усл. Липшица по аргументам (y,y’,…,y(n-1)),
имеет решение, и при том единственное
Д-во
Сведём ⦁ к задаче Коши для нормальной системы. Пусть
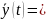 {y1=y(t),y2=y’(t),..,yn=y(n-1)(t)}
{y1=y(t),y2=y’(t),..,yn=y(n-1)(t)}
 o={yo,yo’,…,yo(n-1)}
o={yo,yo’,…,yo(n-1)}
 {y2,y3,…,yn,f(y,y1,y2,…,yn)}
{y2,y3,…,yn,f(y,y1,y2,…,yn)}
Тогда имеем нормальную систему

т.к.
 удовл. усл. т. решения задачи Коши для
норм. систем оду, а) непр. по всем арг. в
области D: (|t-t0|≤T,
|ym-ym0|≤b),
где b-одно
и то же для m∊[1,n];
б)усл. Липшица по
:
удовл. усл. т. решения задачи Коши для
норм. систем оду, а) непр. по всем арг. в
области D: (|t-t0|≤T,
|ym-ym0|≤b),
где b-одно
и то же для m∊[1,n];
б)усл. Липшица по
:
|fm(t, ’)-fm(t, ”)|≤k {|y1’-y1”|+…+|ym’-
-ym”|} для всех m∊[1,n]
следовательно, теорема доказана ∎
6. Ед. Решения з. Коши норм. Системы
Теорема
Если
 ={fm(t,y1,…yn)}
для всех m∊[1,n]
удовл. усл:
={fm(t,y1,…yn)}
для всех m∊[1,n]
удовл. усл:
1)непр по всем арг. в области D: (|t-t0|≤T, |ym-ym0|≤b), где b-одно и то же для m∊[1,n];
2)усл. Липшица по , т.е.:
|fm(t, ’)-fm(t, ”)|≤k{|y1’-y1”|+…+|yn’-yn”|}
для
всех m∊[1,n],
то решение задачи Коши
(t)
для нормальной системы ДУ единственно
на отр. |t-to|<n,
где n=min(T, ),
|fm|<M
для ∀m
),
|fm|<M
для ∀m
Д-во
Необх. д-ть, ед. решения норм. системы ДУ

которой соотв. эквив. система инт. ур.
ym(t)=ymo+ fm(r,y1(r),…,yn(r))dr m∊[1,n] ⦁
Пусть есть 2 решения: (1)={y1(1),…,yn(1)},
(2)={y1(2),…,yn(2)}, у которых не все
ym1
равны ym2.
Тогда не равна нулю ф-ия отклонения
решений Ф(t)=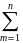 |ym(1)-ym(2)|
|ym(1)-ym(2)|
из ⦁ ⇒ ym(1)-ym(2)= (fm(r, (1))-fm(r, (2)))dr
Используя усл. Липшица для fm(t,y), получим
|fm(r, (1))-fm(r, (2))|≤kФ(r)
Следовательно, |ym(1)-ym(2)|≤k Ф(r)dr
Из полученного н-ва, согласно оценке
0≤Z(t)≤ ,k=const,
получаем Z(t)=0,
имеем Ф(t)=0,
что означает, что
1=
2
∎
,k=const,
получаем Z(t)=0,
имеем Ф(t)=0,
что означает, что
1=
2
∎
7.Устойчивость по первому приближению
Теорема
 Пусть
в некоторой окрестности точки покоя
Пусть
в некоторой окрестности точки покоя
 =0
правая часть автономной системы
=0
правая часть автономной системы
 непр. вместе с производными до второго
порядка включительно. Тогда, если все
λk характ. числа
матрицы Â={aij=
непр. вместе с производными до второго
порядка включительно. Тогда, если все
λk характ. числа
матрицы Â={aij= =0
}
=0
}
удовлетворяют
усл. Reλk<0,
то тривиальное решение системы

Асимптотически устойчиво. Если хотя бы 1 λk имеет Reλk>0, то решение неустойчиво
8. Определение непр. Зависимости решения з.Коши от начального усл.
Пусть
дана задача Коши
 ⦁
⦁
Пусть ф-ия f(t,y) опр. и непр. в прям. Q={(t,y): |t=to|≤T, A≤y≤B}. Непр. зависимость решения задачи Коши от начального условия – это когда решением задачи Коши на отр. [to-T,to+T] явл. ф-ия y(t) такая, что y(t), непр. диф. на [to-T,to+T], A≤y(t)≤B для t∊[to-T,to+T] y(t) удовл. ⦁
Решение задачи Коши ⦁ зависит от ф-ии f(t,y) и начального состояния yo
Теорема
Пусть ф-ии f1(t,y) И f2(t,y) непр. в прям. Q и f1(t,y) удовл. в Q условию Липшица по y, то есть ∃L>0, такая что:
|f1(t,y)-f1(t, )|≤L|y-
|,
∀(t,y),(t,
)∊Q
)|≤L|y-
|,
∀(t,y),(t,
)∊Q
Тогда если ф-ии y1(t) и y2(t) на отр. [to-T,to+T] явл. решениями задачи Коши ⦁, то имеет место н-во
t∊ |y1(t)-y2(t)|≤(|y01-
|y1(t)-y2(t)|≤(|y01-
-y02|+T |f1(t,y)-f2(t,y)|exp{LT}
|f1(t,y)-f2(t,y)|exp{LT}
9. Сингулярное возмущение з. Коши
Сингулярным возмущением задачи Коши
 называется
случай, когда f(y,x,μ)
при μ->0 имеет нерегулярность, т.е. ведёт
себя особым (сингулярным) образом, что
приводит к нарушению условий теоремы
существования и единственности решения.
называется
случай, когда f(y,x,μ)
при μ->0 имеет нерегулярность, т.е. ведёт
себя особым (сингулярным) образом, что
приводит к нарушению условий теоремы
существования и единственности решения.
10. Решение з. Коши импульсной функцией
Пусть o (t) – решение неоднородной системы с нулевыми начальными данными

Тогда
мы можем выразить
 через импульсную ф-ию
через импульсную ф-ию
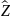 (t,to)=
(t,to)= (t)
-1(to):
(t)
-1(to):
= (t)- (t,to)* o, где
(t) – решение задачи Коши для неодн. системы ДУ
а
o
находится из одн. системы с заданными
начальными данными
где
 (t)
– решение этой системы
(t)
– решение этой системы
11. Условия на f(t,y) для сущ. непр. решения
Если в задаче Коши

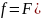

f(t,y,μ) непр. по всем арг. в области D:{0≤t≤T, |y|≤a, |μ-μo|≤b} и удовл. по переменной y усл. Липшица
|f(t,y1,μ)-f(t,y2,μ)|≤k|y1-y2|
всюду в D, причём k не зависит от t и μ, то решение задачи y=y(t,μ) определено в D и непрерывно по t и μ.
13. Что следует,
согласно лемме Гронуолла-Беллмана, из
оценки
, где
 – непрерывная функция?
– непрерывная функция?
Согласно Лемме Г-Б из этого следует оценка Z(t)=0, где Z(t) – непр.
14. Дать определение фундаментальной системы решений для линейной однородной системы дифференциальных уравнений.
Фундаментальной системой решений однородной системы уравнений называется n линейно независимых решений {(k) } , k∊[1,n] этой системы.
15.Дать определение фундаментальной системы решений и фундаментальной матрицы для линейной однородной системы обыкновенных дифференциальных уравнений.
Фундаментальной системой решений однородной системы уравнений называется n линейно независимых решений {(k) } , k∊[1,n] этой системы, а соответственно матрица этих решений ={(1) ,…,(n) } называется фундаментальной матрицей системы
16.Является ли единственной фундаментальная матрица для линейной системы дифференциальных уравнений? Ответ обосновать.
Фундаментальная матрица для лин. системы не явл. единственной. Существует бесконечно много фунд. матриц, т.к. в задаче Коши
достаточно взять
 ,
где Det
,
где Det
 ≠ 0, и получится другая фунд. матрица
≠ 0, и получится другая фунд. матрица
23.Выписать импульсную функцию через фундаментальную матрицу линейной системы.
Импульсная ф-ия (t,to) выражается через фунд. м-цу линейной системы в виде
(t,t0)=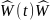 -1(t0)
-1(t0)
24.Запишите общее решение однородной линейной системы дифференциальных уравнений с произвольными начальными данными с помощью фундаментальной матрицы.
Если
(t)
– фунд. матрица, а (0)y(t)
– частное решение y’= y+b,
то общее решение неодн. ур. представимо
в виде: y(t)=
(t)C+(0)y(t)
y+b,
то общее решение неодн. ур. представимо
в виде: y(t)=
(t)C+(0)y(t)
25.Что называется принципом суперпозиции для линейного дифференциального уравнения n-го порядка?
Для линейного ДУ n-го п-ка выполняется принцип суперпозиции, который определяется равенством:

26.Сформулировать теорему об альтернативе для определителя Вронского для решений линейной однородной системы обыкновенных дифференциальных уравнений.
Теорема
Определитель Вронского Δ(t) для решений {(k) }, k∊[1,n] однородной системы ДУ или Δt=0 для ∀t∊r, что означает ЛЗ {(k) }, или Δ(t)≠0 для ∀t∊r, что означает ЛНЗ {(k) }.
27.Дать определение особого решения для обыкновенного дифференциального уравнения 1-го порядка, не разрешенного относительно производной.
Особым решением называется такое решение уравнения, во всех точках которого нарушается единственность решения задачи Коши
28.Дать определение характеристического многочлена для линейного однородного обыкновенного дифференциального уравнения n-го порядка с постоянными коэффициентами.
Рассмотрим линейное однородное уравнение n-го порядка с вещ. постоянными коэф. aj∊R, j=0,…,n, ao≠0:
aoy(n)(t)+a1y(n-1)(t)+…+an-1y’(t)+any(t)=0
 Это
уравнение можно записать в операторном
виде Ly=0,
где дифференциальный оператор L
с постоянными коэф. (!!!L –
прописная !!!!!)
Это
уравнение можно записать в операторном
виде Ly=0,
где дифференциальный оператор L
с постоянными коэф. (!!!L –
прописная !!!!!)
Ly=aoy(n)(t)+a1y(n-1)(t)+…+an-1y’(t)+any(t)
Сопоставим диф. оператору L многочлен
μ(λ)=aoλn+a1λn-1+…+an-1λ+an
многочлен μ(λ) называется характеристическим многочленом
