2.5.2. Расчеты по сечениям наклонным к продольной оси.

Рис 2.10 Схема для расчета по сечениям, наклонным к продольной оси

Расчет ведем для Q=Q_max = 83,15 кН.

Q  Q_{b min} = 0,5R_btbh₀

Где Q_{b min} – наименьшая поперечная сила, воспринимаемая бетоном, кН

Q_{b min} = 0,510³0,6750,390,365 =48,04 кН

Для участка II выбираем конструктивное армирование. Арматура В-500

1) Задаемся: d_sw >= d/4 = 16/4 =4 мм принимаем d_sw = 4 мм.

2) Принимаем шаг 250мм

S=3h₀/4=3*365/4=273 мм.

Для участков I и III (83,15 кН > Q_{b min} = 48,04)  армирование выбираем расчетом.

1) Задаемся: d_sw >= d/4 = 16/4 =4 мм принимаем d_sw = 5 мм.

2) Принимаем шаг 150мм

S=h₀/2=365/2=182,5 мм.

3) Определяем интенсивность хомутов:

q_sw=(R_sw*A_sw1*n)/S≥0,25 R_btb

где A_sw1=0,196 см² – площадь одного стержня;

n=5 – число каркасов.

q_sw = (300*10³*0,126*10^-4*5)/0,15 =126 кН/м ≥ 0,25*0,675*10^3*0,39=65,81 кН/м

4) Определяем длину проекции опасной наклонной трещины на продольную ось:

с_о = (1,5R_btbh₀² / 0,75q_sw)^1/2

с_о = (1,50,67510³0,380,365² / 0,75126) ^1/2 =0,72 м.

h_о=0,365 м < с_о =0,72 м < 2* h_о=0,73 м.

5) Определяем поперечную силу, воспринимаемую бетоном:

Q_в = 1,5R_btbh₀² / с_о =1,50,67510³0,390,365² /0,72 =73,07 кН.

6) Определяем поперечную силу, воспринимаемую хомутами:

Q_sw = 0,75* q_sw * с_о =0,75*126 *0,72 =68,04 кН.

7) Проверяем условие:

Q ≤ Q_в +Q_sw =68,04 +73,07 =141,11 кН.

Q = 83,15 кН <141,11 кН. условие выполнено.

9) Проверяем условие:

Q= 83,15 кН 1,5R_btbh₀² /S=1,50,67510³0,390,365² /0,15=350,71кН условие выполнено.

2.5.3 Расчеты на местное действие нагрузок

Для плит с круглыми пустотами прочность полки всегда обеспечена и армируется она конструктивно.

Принимаем сетку С-1 .

2.6. Расчеты панели по II группе предельных состояний.

2.6.1. Геометрические характеристики приведенного сечения.

При расчете панели по предельным состояниям II группы расчетное сечение панели приводится к эквивалентному двутавровому. Действительные пустоты заменяются прямоугольными с теми же моментами инерции и площадями. Центры тяжести исходных пустот и прямоугольников должны совпадать.

Разбиваем приведенное сечение на правильные прямоугольники.

Рис. 2.11 Приведенное двутавровое сечение.

y₁=367,5 мм; y₂=200 мм, y₂=32,5

1) Определяем площадь приведенного сечения.

где A_sb – эквивалентная площадь арматуры, см²;

A_s – площадь арматуры, см²;

 - коэффициент приведения;

E – модуль упругости;

A_red – приведенная площадь сечения панели, см²;

A_b – площадь бетона, см².

_Ab=7,1*143,6*2+8,2*25,8*3+7,9*26*2=3084,6 см²

2) Определяем статический момент приведенного сечения.

где S_red – статический момент приведенного сечения панели, см³;

y_i – расстояние от центра тяжести приведенного сечения до нижней грани элемента, см.

3) Определяем положение центра тяжести приведенного сечения.

где y₀ – положение центра тяжести всего приведенного сечения, см.

4) Определяем момент инерции приведенного сечения.

где I_red – момент инерции приведенного сечения, см⁴.

5) Определяем момент сопротивления приведенного сечения.

где – момент сопротивления приведенного сечения, см³.

2.6.1 Расчеты трещиностойкости сечений нормальных к продольной оси

Трещины не образуются, если выполняется условие:

где - момент от нормативной полной нагрузки;

- изгибающий момент, при котором образуются трещины:

где - сопротивление бетона растяжению для второй группы предельных состояний.

Пластический момент сопротивления:

где

- коэффициент который учитывает влияние неупругих деформаций бетона растянутой зоны в зависимости от формы сечения. Для симметричного двутаврового сечения при 2 < b_f/b=1436/390=3,68  6

Условие не выполняется, следовательно, необходимо произвести расчет на раскрытие трещин.

Условие по раскрытию трещин:

где - ширина раскрытия трещин;

- предельно-допустимая ширина раскрытия трещин.

Нормами ограничивается раскрытие трещин:

- для продолжительного раскрытия: ;

- для непродолжительного раскрытия:

Определяем величину продолжительного раскрытия трещин:

где - ширина раскрытия трещин от продолжительного действия постоянных и временных длительных нагрузок.

где - коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами. Допускается принимать ;

- коэффициент, учитывающий продолжительность действия нагрузки. Для продолжительного действия нагрузки ;

- коэффициент, учитывающий профиль продольной арматуры. Для арматуры периодического профиля ;

- коэффициент, учитывающий характер нагружения. Для изгибаемого элемента ;

- модуль упругости стали, ;

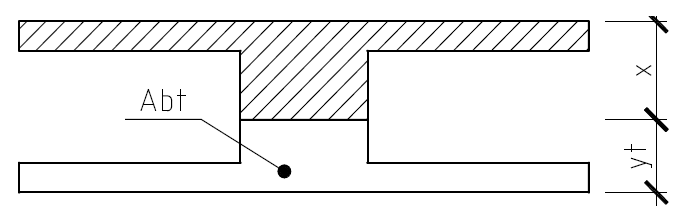
Рисунок 2.12 – Растянутая и сжатая зоны приведенного сечения

где - площадь сечения растянутого бетона. Для двутавровых сечений:

где - расстояние до центра тяжести приведенного сечения:

Определяем высоту растянутой зоны бетона (рисунок 2.12):

где k – поправочный коэффициент, для двутавровых сечений k=0,95.

,

- площадь продольной арматуры, ;

– диаметр продольной арматуры, .

,

Необходимо выполнение условий:

:

:

Условия не выполняются, берем граничное значение .

– напряжение в растянутой арматуре:

где - момент от действия длительных нагрузок, ;

- расстояние от центра тяжести растянутой арматуры до равнодействующей усилий в сжатой зоне:

Ширина раскрытия трещин превышает допустимые 0,3 мм. Увеличиваем диаметр продольной арматуры.

Принимаем пять стержней диаметром 22 мм, .

Тогда:

,

Условия не выполняются, берем граничное значение .

Условие выполняется.

Определяем величину непродолжительного раскрытия трещин:

где - ширина раскрытия трещин от непродолжительного действия постоянных и полных временных нагрузок.

где ; для непродолжительного действия нагрузки ; для арматуры периодического профиля ; для изгибаемого элемента ;

,

Необходимо выполнение условий:

:

:

Условия не выполняются, берем граничное значение .

апряжение в растянутой арматуре:

где - момент от действия полных нагрузок, ;

- ширина раскрытия трещин от непродолжительного действия постоянных и временных длительных нагрузок.

; для непродолжительного действия нагрузки ; для арматуры периодического профиля ; ля изгибаемого элемента ;

апряжение в растянутой арматуре:

где - момент от действия длительных нагрузок, ;

Определяем величину непродолжительного раскрытия трещин:

Условие выполняется.

2.6.4. Расчеты прогибов

Расчет железобетонных элементов по прогибам производят из условия:

где fu - предельно допустимый прогиб, определяемый по таблице 19 СНиП 2.01.07-86* «Нагрузки и воздействия».

Различают 2 вида прогибов:

- длительный прогиб. Возникает от длительного воздействия нагрузок, предельное значение [f]lрегламентируется СНиП 2.01.07-86* «Нагрузки и воздействия» и зависит от вида конструкции: для покрытий и перекрытий при наличии на них элементов. Подверженных растрескиванию (стяжек, полов, перегородок) [f]l= l/150=6760/150=45 мм.

- полный прогиб. Возникает от действия всей нагрузки, предельное значение

[f]= l/200=6760/200=33,8 мм

где l – пролет конструкции.

Определение прогибов выполняют в зависимости от наличия или отсутствия трещин. По упрощенной форме прогиб можно найти следующим образом:

,

где – соответствующая кривизна, при которой определяется прогиб;

_S– коэффициент, учитывающий характер нагрузки, для равномерно распределенной нагрузки _S= ;

l₀ – расчетный пролет, в нашем случае - расстояние между серединами площадок опирания плиты.

Полная кривизна для участков с трещинами в растянутой зоне определяется:

где - кривизна от непродолжительного действия полных нагрузок;

- кривизна от непродолжительного действия постоянных и временных длительных нагрузок;

- кривизна от продолжительного действия постоянных и временных длительных нагрузок.

Значение полного прогиба определяем от полной кривизны, значение длительного прогиба – только от , то есть кривизны от продолжительного действия постоянных и временных длительных нагрузок:

Кривизну железобетонного элемента на участках с трещинами определяем по формуле:

гдеM_i - момент, от действия которого определяется кривизна;

- приведенный модуль деформации сжатого бетона при заданном действии нагрузки (продолжительном/непродолжительном)

- момент инерции приведенного сечения относительно его центра тяжести.

где - относительная деформация бетона при заданном действии нагрузки.

где I_bиI_s – момент инерции площадей сечения соответственно сжатой зоны бетона и растянутой арматуры относительно центра тяжести приведенного без учета бетона растянутой зоны поперечного сечения;

- коэффициент приведения растянутой арматуры к бетону.

где х – высота сжатой зоны бетона;

А’_f – площадь сечения свесов сжатой полки,

Высота сжатой зоны (Рисунок 2.13) тавровых сечений может быть определена по формуле:

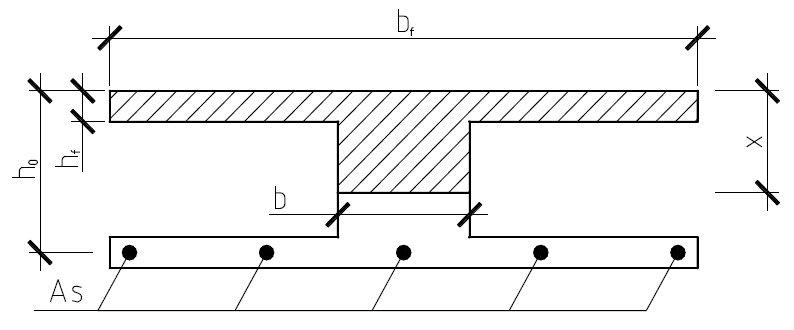
Рисунок 2.13 – К расчету момента инерции приведенного сечения

Определяем кривизну от непродолжительного действия полных нагрузок

Определяем кривизну от непродолжительного действия постоянных и временных длительных нагрузок

Определяем кривизну от продолжительного действия постоянных и временных длительных нагрузок

 = ₁ – ₂ + ₃=3,26-4,7+6,2=4,76 мм < 33,8 мм

Условие выполняется.

2.7. Проверка панели на нагрузки при транспортировке и монтаже.

Для монтажа и транспортировки панели в ней предусматривают четыре монтажные петли из арматуры класса АI. Закладываются петли на расстоянии 0,7 м от концов панели.

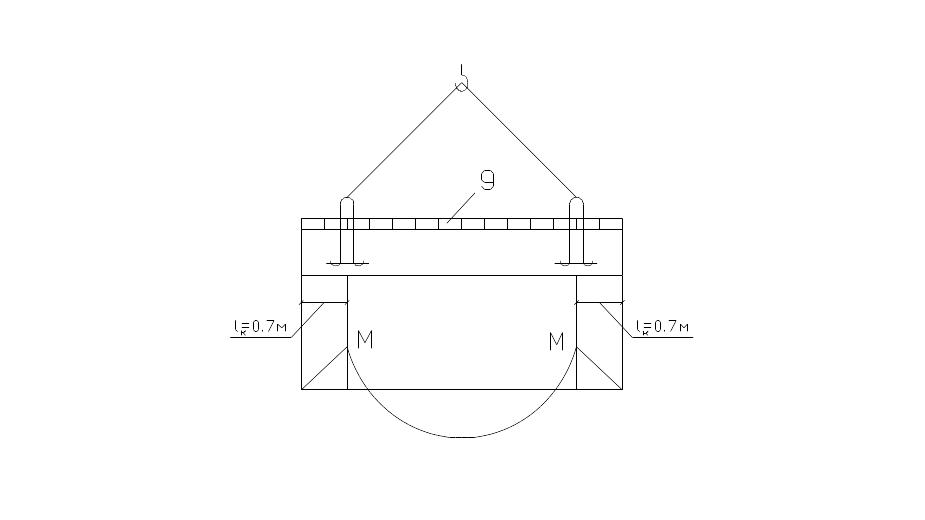
Рис 2.13 Транспортировка панели

Под монтажными петлями в плите расположены горизонтальные стержни.

где q – нагрузка от собственного веса плиты на 1 м²;

k_d – коэффициент динамичности.

где h₀ = h – a= 0,4 – 0,035 = 0,365 м

h = 0,9

R_s=215 МПа – класс арматуры монтажной А240.

По A_s принимаем два горизонтальных стержня d = 6 мм и A_{s ф} = 57 мм²

2.8. Расчет монтажных петель.

Рассчитаем диаметр петель.

При подъёме вся нагрузка передаётся на 2-е петли:

Усилие на одну петлю: ;

Принимаем 1 петлю AI диаметром 18 мм, с A_ф=254,5 мм².

2.9 Конструирование плиты перекрытия

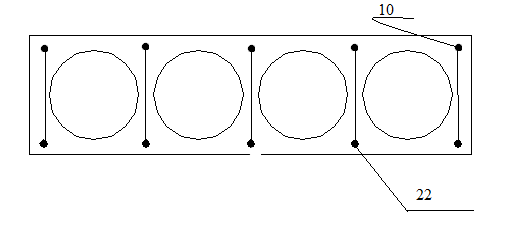
Рисунок 2.14 – Поперечный разрез плиты

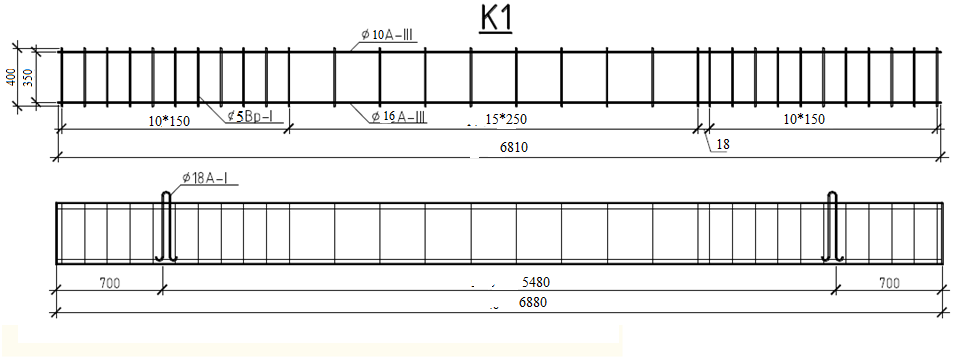
Рисунок 2.15 – Продольный разрез плиты