Графічне зображення розподілу ілюструє

Рис. Зони автокореляційного зв’язку за критерієм Дарбіна - Уотсона

16. Тестуваннагетероскедастичності залишків

Ще один тест для перевірки гетероскедастичності запропонував Глейсер: розглядати регресію абсолютних значень залишків , які відповідають регресії найменших квадратів як деяку функцію від , де є тією незалежною змінною, яка відповідає зміні дисперсії . Для цього використовуються такі види функцій:

1) ;

2) ;

3) і т.п.

Рішення про відсутність гетероскедастичності залишків приймається на основі статистичної значущості коефіцієнтів й . Переваги цього тесту визначаються можливістю розрізняти випадок чистої і змішаної гетероскедастичності. Чистій гетероскедастичності відповідають значення параметрів , ; а змішаній — , . Залежно від цього треба користуватись різними матрицями . Нагадаємо, що:

.

Якщо при економетричному моделюванні для певних вихідних даних буде виявлено явище гетероскедастичності, то оцінку параметрів моделі треба виконувати на основі узагальненого методу найменших квадратів. Оператор оцінювання цим методом запишеться:

,

де

.

В даній матриці залежно від висунутої гіпотези:

або ;

або ;

або .

Прогноз на основі економетричної моделі, в якій оцінка параметрів виконана узагальненим методом найменших квадратів, можна отримати на основі такого співвідношення:Ω^-1

,

де u — вектор залишків, який відповідає оцінці параметрів моделі на основі 1МНК;

— транспонований вектор коваріацій поточних і прогнозних значень залишків;

, а .

17. Узагальнений метод найменших квадратів (метод Ейткена)

Оператор оцінювання УМНК можна записати так:

де Ω^-1-матриця, обернена до дисперсійно-коваріаційної матриці залишків Ω.

На практиці для розрахунку ρ використовується співвідношення

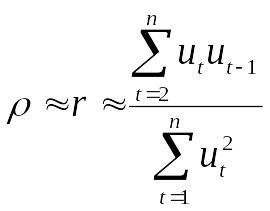або

Економетрична модель, якійпритаманнагетероскедастичність, є узагальненоюмоделлю, і для оцінюванняїїпараметрівслідскористатисяузагальненим методом найменшихквадратів. Розглянемоцей метод.

Нехай задано економетричну модель

(7.1)

коли .

Задача полягає в знаходженніоцінокелементів вектора А в моделі. Для цьоговикористовуєтьсяматрицяS, за допомогоюякоїкоригуєтьсявихіднаінформація. Цяідеябулапокладена в основу методу Ейткена.

Базуючись на особливостяхматрицьР і S, якібулирозглянуті в підрозд. 7.3, можназаписатиспіввідношенняміжцимиматрицями та оберненими до них.

ОскількиS — додатновизначенаматриця, то вона може бути зображена як добуток , де матрицяP є невиродженою, тобто:

, (7.2) коли

; (7.3) і

. (7.4)

Помноживши рівняння (7.1) ліворуч на матрицю ,дістанемо:

. (7.5)

Позначимо ;

;

.

Тоді модель матимевигляд:

. (7.6)

Використовуючи (7.3), неважкопоказати, що

,

тобто модель (7.6) задовольняєумови (4.2), коли параметримоделіможнаоцінити на основі 1МНК.

Звідси

. (7.7)

Цяоцінка є незміщеноюлінійноюоцінкою вектора А, якиймаєнайменшудисперсію і матрицюковаріацій

(7.8)

Hезміщенуоцінку для дисперсії можнадістати так:

(7.9)

Оцінкапараметрів , яку знайдено за допомогою (7.7), є оцінкоюузагальненого методу найменшихквадратів (методу Ейткена).

При заданійматриціSоцінкупараметрівмоделіможнаобчислитизгід­ноіз (7.7), а стандартнупомилку — згідноіз (7.8). Тому можнасконструю­ватизвичайнікритеріїзначущості і довірчіінтервали для параметрів .

Визначившизалишки і помноживши ліворуч на матрицю , дістанемо:

,

або .

Звідси .

Тоді .

Оскільки ,

то (7.10)

Отже, ми розбилизагальну суму квадратів для (7.6) на суму квадратіврегресії і залишкову. Згідно з цимиданимидисперсійнийаналіз буде виконано для перетворенихвихіднихданих. Крім того, коли незалежназмінна вимірянавідносно початку відліку, а не у формівідхиленнявідсередньої, то необхідновизначитиїїсереднєзначення і скористатись ним для корекціїзагальноїсумиквадратів і сумиквадратіврегресії.

Модель узагальненого методу найменшихквадратівінодіспецифі­кується у вигляді

(7.11)

де —відомасиметричнадодатновизначенаматриця. Тодівираз для оцінкипараметрівзгідно з методом Ейткеназапишеться так:

, (7.12)

а для їїковаріаційноїматриці

. (7.13)