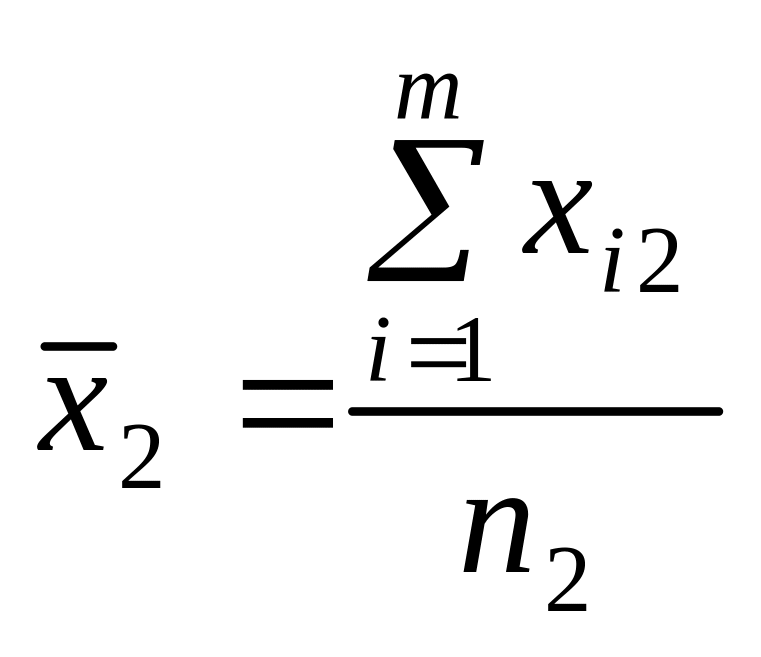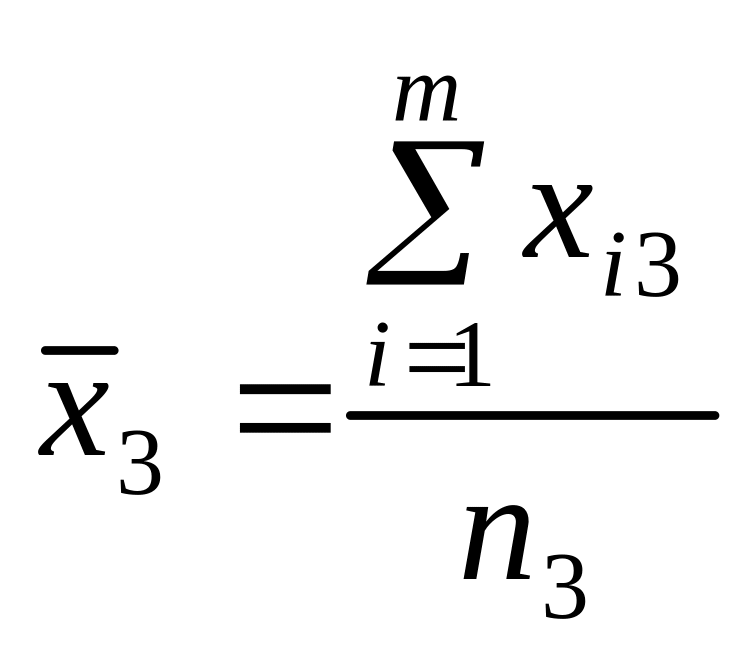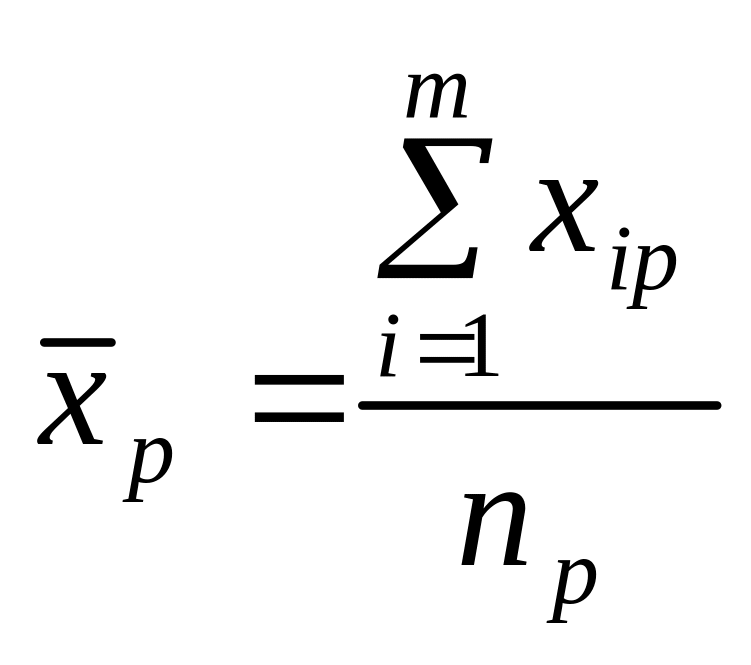41. Емпірична функція розподілу, її властивості та графік

Емпірична функція розподілу - це функція розподілу реалізації випадкової величини, яку будують за результатами вимірювань (спостережень).Нехай маємо випадкову величину  , де n - загальна кількість спостережень. Через v_k(x) позначимо випадкову величину, яка дорівнює кількості елементів вибірки ξзначення яких менше x. Тоді емпірична функція розподілу буде задаватись як  .Для побудови таблиці значень емпіричної функції розподілу використовують такий метод. Спочатку всі результати спостережень впорядковують за зростанням й визначають їх ранги (порядкові номера в отриманої послідовності). Потім кожному спостереженню приводять у відповідність число  .Графік емпіричної функції розподілу має східчастий вигляд. Із збільшенням кількості спостережень він стає більш гладким, а емпірична функція розподілу наближається до теоретичноїфункції розподілу генеральної сукупності чи певної теоретичної моделі розподілу.

Нехай маємо статистичний розподіл вибірки обсягу . Позначимо - кількість спостережень, при яких спостерігали значення ознаки менше числа . Відносна частота події буде . Із зміною змінюється і відносна частота, тобто відносна частота є функцією від .Функцією розподілу вибірки називають функцію , яка визначає для кожного значення відносну частоту події : = , (1)

де - число варіант, менших .

Її ще називають емпіричною функцією розподілу, оскільки вона шукається емпіричним (дослідним) шляхом.

42.Вибіркове середнє значення визначається як середнє арифметичне варіант з урахуванням їх частот Хв-1\n сума хі niВластивості:1.Якщо зб або зм , ото виб. Середнє …2. зб або зм в певну кількість , то виб сер. …3. сер. Відхилення = 0 4. Сер алгебр сума двох величин= алгебр сумі середніх. Степеневе середнє це величина частот Хв-1\n сума хі ni тільки до квадрату. Мода - це варіанта, що має найб частоту. Медіана – варіанта, що ділить ряд розп. Навпіл.

43.

44. Точкові та інтервальні статистичні оцінки Статистична оцінка яка визначається одним числом, точкою, називається точковою. Беручи до уваги, що є випадковою величиною, точкова статистична оцінка може бути зміщеною і незміщеною: коли математичне сподівання цієї оцінки точно дорівнює оцінювальному параметру θ, а саме: (1) то називається незміщеною; в противному разі, тобто коли точкова статистична оцінка називається зміщеною відносно параметра генеральної сукупності θ. Різниця (3) називається зміщенням статистичної оцінки Оцінювальний параметр може мати кілька точкових незміщених статистичних оцінок Точкова статистична оцінка називається ефективною, коли при заданому обсязі вибірки вона має мінімальну дисперсію. Отже, оцінка буде незміщеною й ефективною.

Точкова статистична оцінка називається ґрунтовною, якщо у разі необмеженого збільшення обсягу вибірки наближається до оцінювального параметра θ, а саме: Точкові статистичні оцінки є випадковими величинами, а тому наближена заміна θ на часто призводить до істотних похибок, особливо коли обсяг вибірки малий. У цьому разі застосовують інтервальні статистичні оцінки. Статистична оцінка, що визначається двома числами, кінцями інтервалів, називається інтервальною. Різниця між статистичною оцінкою та її оцінювальним параметром θ, взята за абсолютним значенням, називається точністю оцінки, а саме: (04) де δ є точністю оцінки. Оскільки є випадковою величиною, то і δ буде випадковою, тому нерівність (04) справджуватиметься з певною ймовірністю. Імовірність, з якою береться нерівність (04), тобто , (05) називають надійністю. Рівність (05) можна записати так: . Інтервал ,

що покриває оцінюваний параметр θ ге­неральної сукупності з заданою надійністю , називають довірчим.

45. Суть методу полягає в пошуку мах значення функції, найб правдоподібності. Дана функція залежить від результатів спостереження чи від параметру, що оцінюється.

Щоб від добутку перейти до суми потрібно пролог рифмувати. Для спрощення процедури для пошуку L. Оцінка що мах логарифм функції правдоп. Наз. Оцінкою методу мах правдоподібності.

46. Метод найм. КВ.є базовим для регресійно корелят. Аналізу. Суть полягає в мінімізації суми квадрат. Відхилень вибірки від досліджуванної величини, тобто необхідно знайти таку оцінку параметру, що мінімізує функцію мети.

Переваги: зрозуміла суть,легкі розрахунки,гарні статистичні властивості,всі оцінки є обґрунтованими.

47. Побудова довірчого інтервалу заданої нерівності для генеральної середньої за допомогою нер Чебишева. Довірчим або надійним інтервалом для оцінки наз інтервал … що містить невідомий параметр. З наперед заданої ймовірності J/ J –наз рівнем надійності, довірності. І = як праило 0,9;0,99.J вибирають аба досліджують самостійно. Чим тервальна оцінка є неближче вона ло 1 тим ширші межі інтервалу. Зауваження: Як правило інтервальна оцінка є симетричною відносно точкової незсунутої оцінки. Жовірчий інтервал ждля параметрів норм. Розподілу за відмою сигма(Д(х)) Нехай х має норм. Розподіл з параметром а та сигма. Сигма- відоме,тоді надійний інтервал, що з рівнем надійності гамма, покриває невідомий парламент а, має межі:

48. Критерій узгодженості Пірсона. Критерій узгодженості Пірсона є випадковою величиною, що має розподіл , який визначається за формулою і має k = q – m –  1 ступенів свободи, де q — число часткових інтервалів інтервального статистичного розподілу вибірки; m — число параметрів, якими визначається закон розподілу ймовірностей генеральної сукупності згідно з нульовою гіпотезою. Так, наприклад, для закону Пуассона, який характеризується одним параметром , m = 1, для нормального закону m = 2, оскільки цей закон визначається двома параметрами i . Якщо (усі емпіричні частоти збігаються з теоретичними), то , у противному разі . Визначивши при заданому рівні значущості  і числу ступенів свободи критичну точку , за таблицею (додаток 8) будується правобічна критична область. Якщо виявиться, що спостережуване значення критерію , то Н0 про закон розподілу ознаки генеральної сукупності відхиляється. У противному разі Н0 приймається.

49. Однофакторний аналіз. Нехай потрібно дослідити вплив на ознаку Х певного одного фактора. Результати експерименту ділять на певне число груп, які відрізняються між собою ступенем дії фактора.

Для зручності в проведенні необхідних обчислень результати експерименту зводять в спеціальну таблицю:

Ступінь впливу фактора (групи)	Спостережуване значення ознаки Х	Групові середні	Загальна середня
1			,
2
3
….	…	…
Р
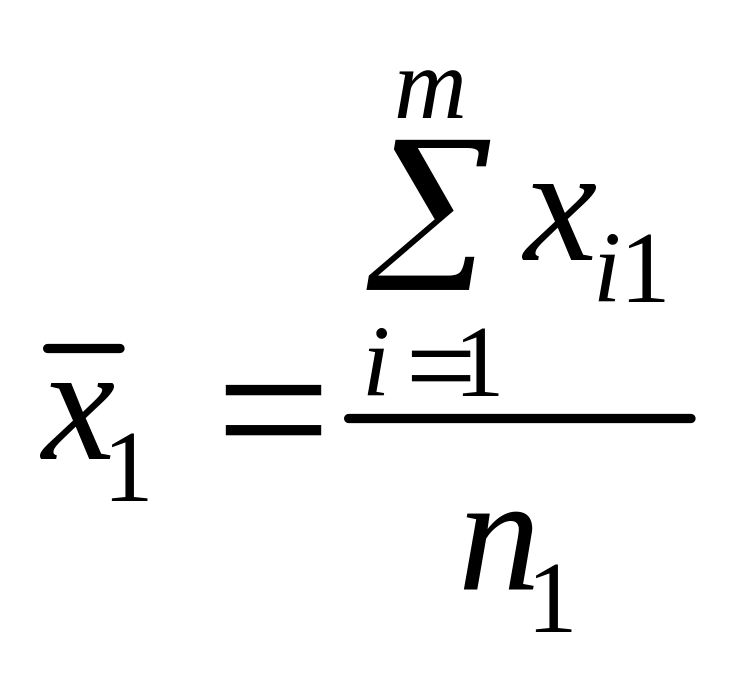
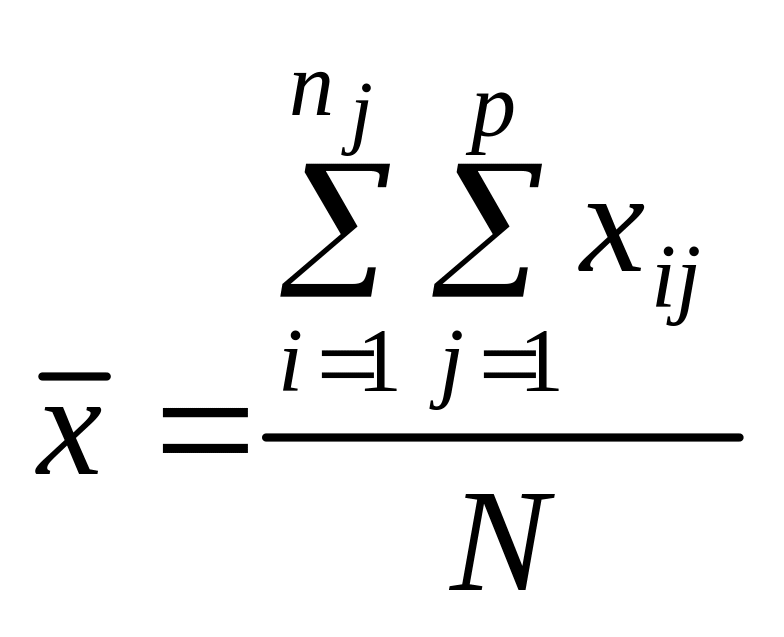