17. Дисперсия света. Нормальная и аномальная дисперсии. Связь групповой и

Д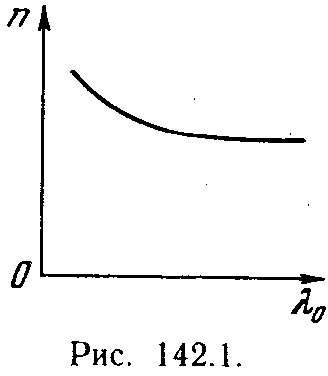 исперсией света называются явления, обусловленные зависимостью показателя преломления вещества от длины све­товой волны. Эту зависимость можно охарактеризовать функцие n=f(lambda0) где lambda0 — длина световой волны в вакууме. Дисперсией вещества называется производная n по lambda0. Для всех прозрачных бесцветных веществ функция (142.1) имеет в видимой части спектра характер, показанный на рис. 142.1. С уменьшением длины волны показатель пре­ломления увеличивается со все возрастаю­щей скоростью, так что дисперсия вещества отрицательна и растет по модулю с уменьшением lambda0.

Если вещество поглощает часть лучей, то в области поглощения и вблизи нее ход дис­персии обнаруживает аномалию (см. рис. 144.2). На некотором участке дисперсия ве­щества оказывается положительной. Такой ход зависимости n от lambda0 называется аномальной дисперсией. Среды, обладающие дисперсией, называются дисперги­рующими. В диспергирующих средах скорость световых волн зависит от длины lambda0 или частотыw.

Строго монохроматическая волна вида представляет собой бесконечную во времени и в пространстве после­довательность «горбов» и «впадин», перемещающихся вдоль оси х v=w/k С помощью такой волны нельзя передать никакого сигнала, так как каждый последующий «горб» ничем не отличается от предыдущего. Для передачи сигнала нужно на волне сделать «отметку», скажем, оборвав ее на некоторое время deltat. Однако в этом случае волна уже не будет описываться уравне­нием (143.1).

П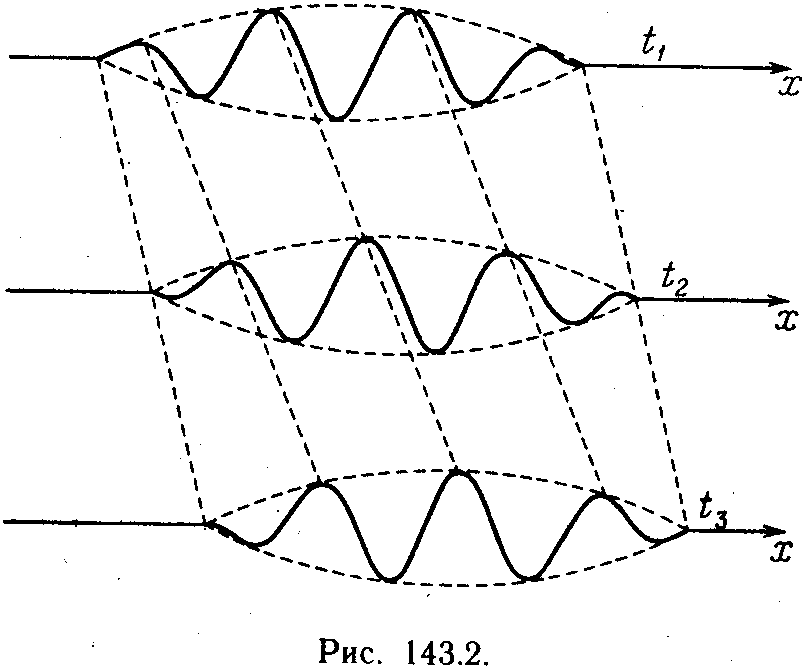 роще всего передать сигнал с помощью светового импульса (рис. 143.1). Согласно теореме Фурье подобный импульс можно представить как наложение волн вида (143.1) с частотами, заклю­ченными в некотором интервале deltaw. Суперпозиция волн, мало от­личающихся друг от друга по частоте, называется волновым пакетом или группой волн. Аналитическое выражение для группы волн имеет вид 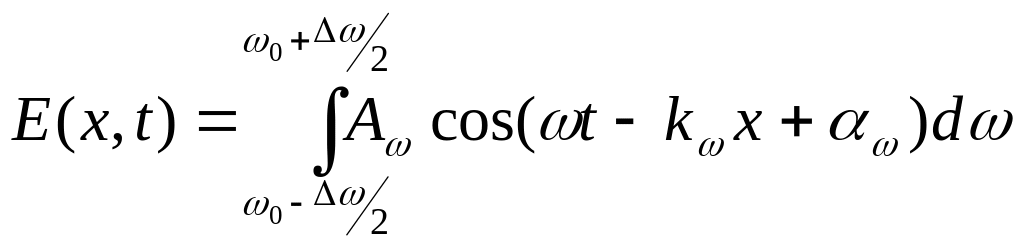(индекс w при A, K и alpha указывает на то, что эти величины для раз­ных частот различны). При фиксированном t график функции (143.3) имеет вид, показанный на рис. 143.1. С изменением t график смещается вдоль оси х. В пределах пакета плоские волны в боль­шей или меньшей степени усиливают друг друга, вне пакета они практически полностью гасят друг друга. Соответствующий расчет дает, что чем меньше ширина пакета deltax, тем больший интервал частот deltaw или соответственно больший интервал волновых чисел deltaw требуется для того, чтобы описать пакет с помощью выражения (143.3). Имеет место соотношение Подчеркнем, что для того, чтобы суперпозицию волн, описываемую выражением (143.3), можно было считать группой волн, необходи­мо соблюдение условия deltaw<<w0. В недиспергирующей среде все плоские волны, образующие пакет, распространяются с одинаковой фазовой скоростью v. Оче­видно, что в этом случае скорость движения пакета совпадает с v и форма пакета со временем не изменяется. Можно показать, что в диспергирующей среде пакет с течением времени расплывается — ширина его увеличивается. Если дисперсия невелика, расплывание пакета происходит не слишком быстро. В этом случае пакету можно приписать скорость и, под которой понимается скорость, с которой перемещается центр пакета, т.е. точка с максимальным значени­ем E. Эту скорость называют групповой скоростью. В диспергирующей среде групповая скорость u отличается от фа­зовой скорости v (имеется в виду фазовая скорость гармонической составляющей с максимальной амплитудой, иными словами — фазовая скорость для доминирующей частоты). На рис. 143.2 показаны «фотографии» волнового пакета для трех последовательных моментов времени t1, t2 и t3. Рисунок выполнен для случая, когда u<v. Из рисунка видно, что наряду с пе­ремещением пакета происходит движение «горбов» и «впадин» «внутри» пакета, причем у левой границы пакета все время зарождаются новые «горбы», которые, пробежав вдоль пакета, исчезают у его правой границы. В результате, в то время как пакет в целом перемещается со скоростью u, отдельные «горбы» и «впадины» перемещаются со скоростью v. когда u>v, перемещения противоположные.