
1. Найти пределы функций
1)![]() 2)
2)![]() 3)
3)![]()
4)![]() 5)
5)![]()
2. Исследовать на непрерывность и построить графики функций
1)
2)![]()
Вариант18
1. Найти пределы функций
1)![]() 2)
2)![]() 3)
3)![]()
4)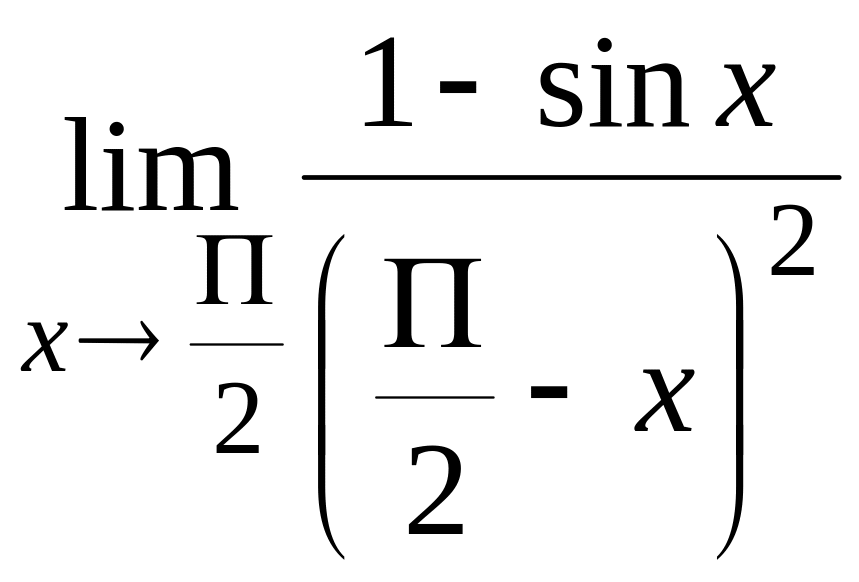 5)
5)![]()
2. Исследовать на непрерывность и построить графики функций
1)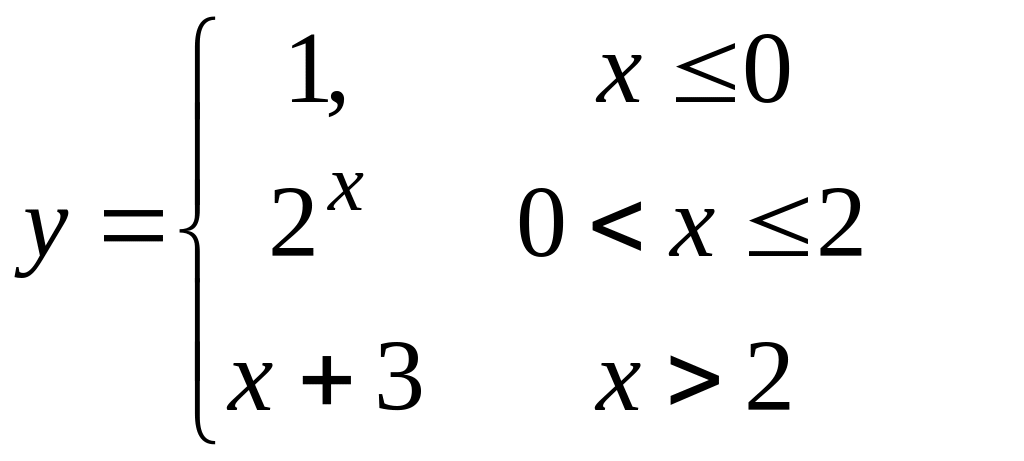
2)
![]() в т.
в т.
![]()
Вариант19
1. Найти пределы функций
1)![]() 2)
2)![]() 3)
3)![]()
4)![]() 5)
5)![]()
2. Исследовать на непрерывность и построить графики функций
1)![]() 2)
2)![]()
Вариант20
1. Найти пределы функций
1)![]() 2)
2)![]()
3)![]() 4)
4)![]()
5)![]()
2. Исследовать на непрерывность и построить графики функций
1)![]()
2)
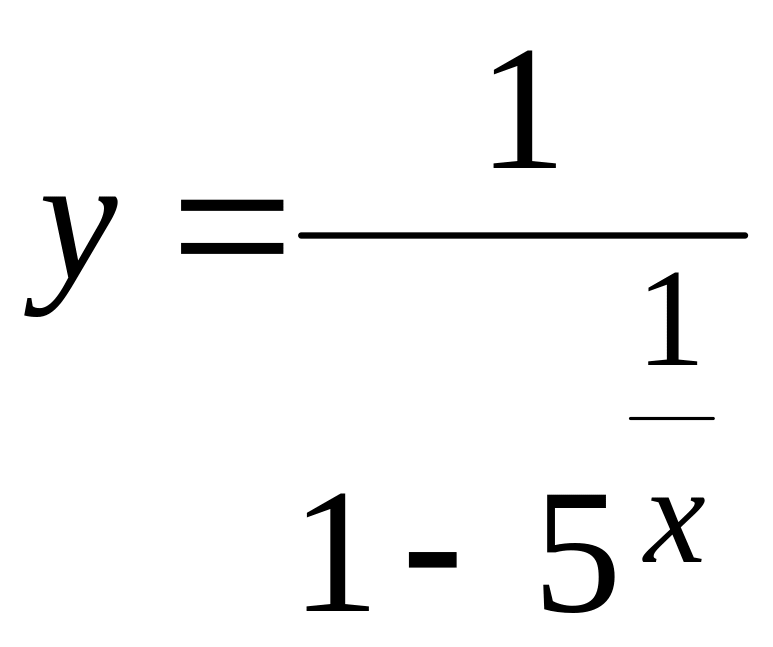 в т.
в т.
Вариант21
1. Найти пределы функций
1)![]() 2)
2)![]() 3)
3)![]()
4)![]() 5)
5)![]()
2. Исследовать на непрерывность и построить графики функций
1)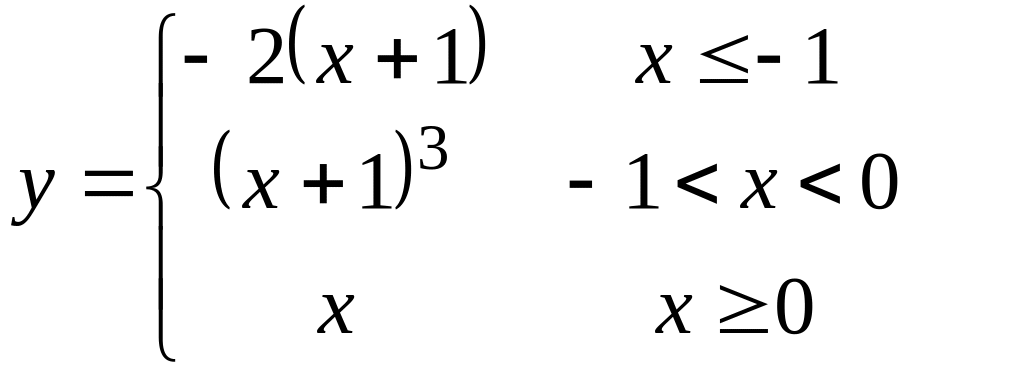
2)
![]() в т.
в т.
![]()
Вариант22
1. Найти пределы функций
1)![]() 2)
2)![]()
3)![]() 4)
4)![]() 5)
5)![]()
2. Исследовать на непрерывность и построить графики функций
1)![]()
2)![]() в т.
в т.
![]()
Вариант23
1. Найти пределы функций
1)![]() 2)
2)![]() 3)
3)![]()
4)![]() 5)
5)![]()
2. Исследовать на непрерывность и построить графики функций
1)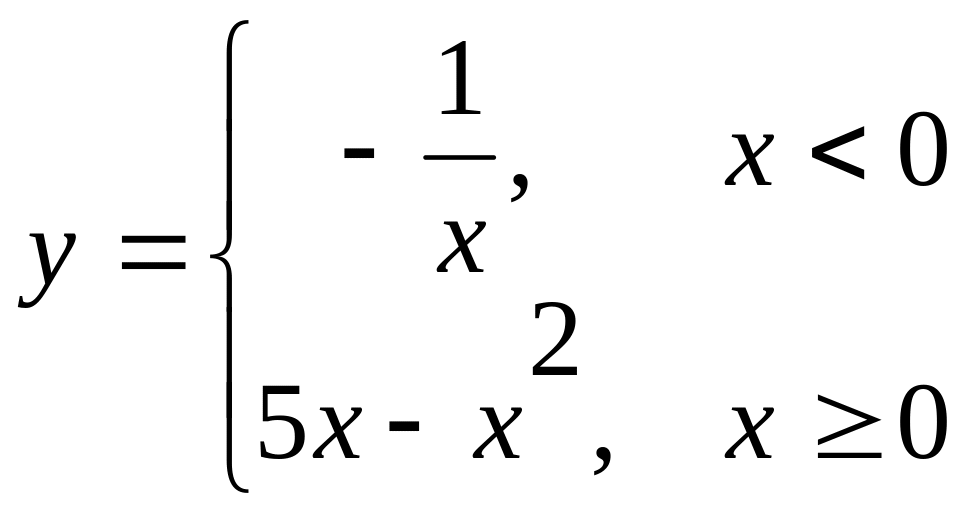
2)
![]() в т.
в т.
![]()
Вариант24
1. Найти пределы функций
1)![]() 2)
2)![]()
3)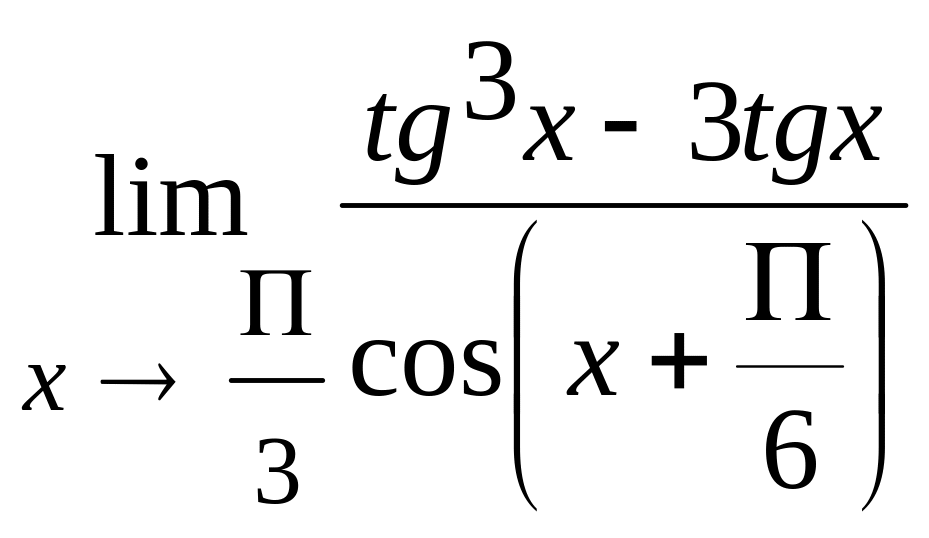 4)
4)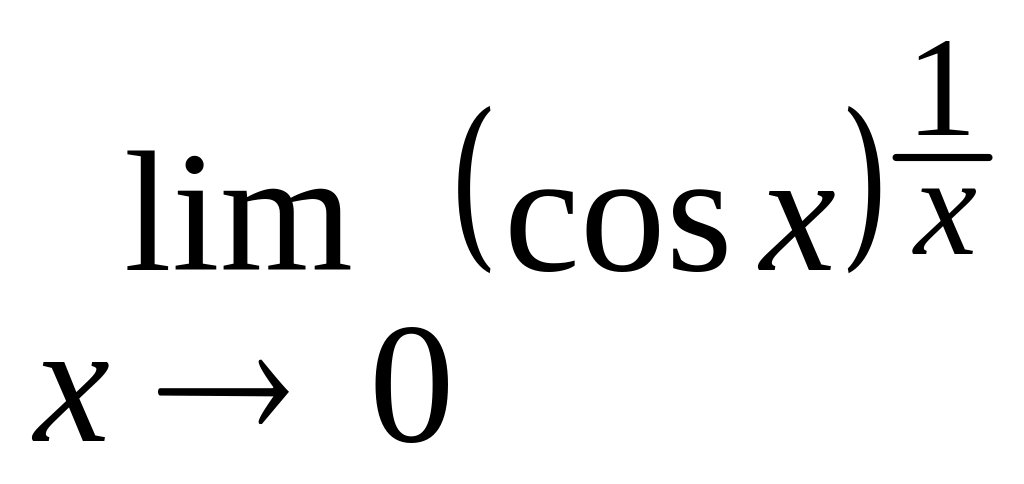 5)
5)![]()
2. Исследовать на непрерывность и построить графики функций
1)
2)![]() в т.
в т.
![]()
Вариант 25
1. Найти пределы функций
1)![]() 2)
2)![]() 3)
3)![]()
4)![]() 5)
5)![]()
2. Исследовать на непрерывность и построить графики функций
1)![]()
2)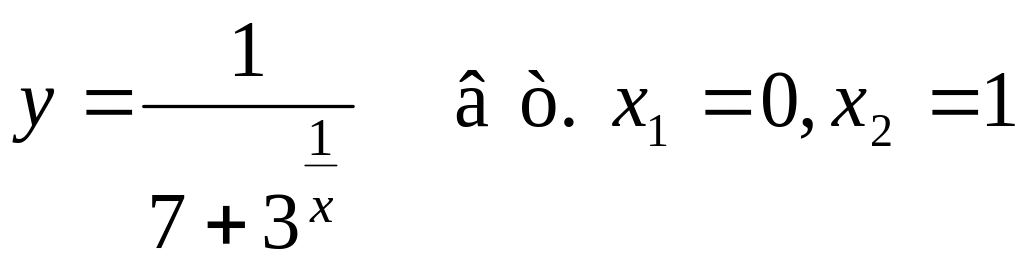
Вариант 26
1. Найти пределы функций
1)![]() 2)
2)![]() 3)
3)![]()
4)![]() 5)
5)![]()
2. Исследовать на непрерывность и построить графики функций
1)
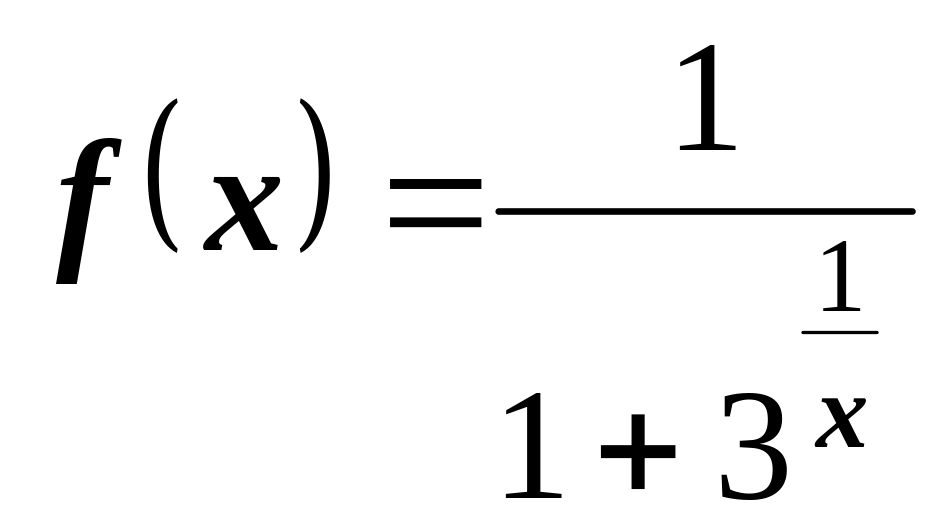 в т.
в т.
2)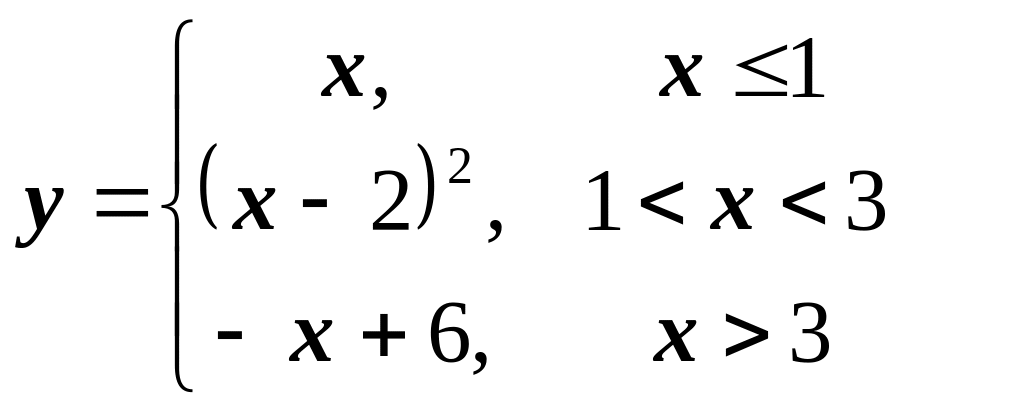
Вариант 27
1. Найти пределы функций
1)![]() 2)
2)![]() 3)
3)![]()
4)![]() 5)
5)![]()
2. Исследовать на непрерывность и построить графики функций
1)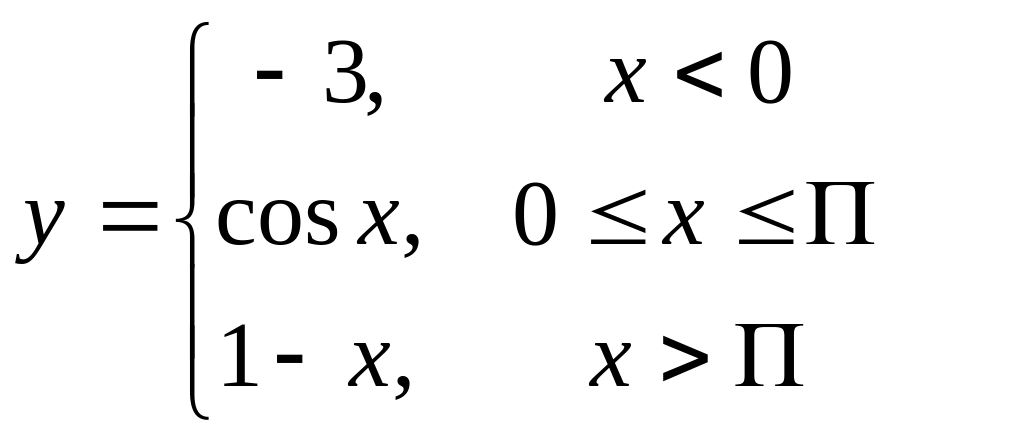
2)
![]() в т.
в т.
Вариант 28
1. Найти пределы функций
1)![]() 2)
2)![]() 3)
3)![]()
4)![]() 5)
5)![]()
2. Исследовать на непрерывность и построить графики функций
1)
![]() в т.
в т.
2)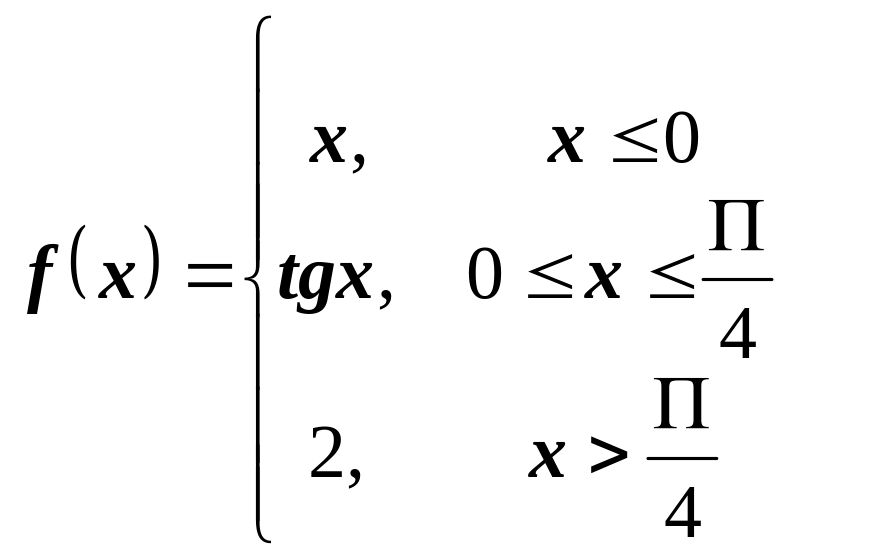
Вариант 29
1. Найти пределы функций
1)![]() 2)
2)![]() 3)
3)![]()
4)
5)![]()
2. Исследовать на непрерывность и построить графики функций
1)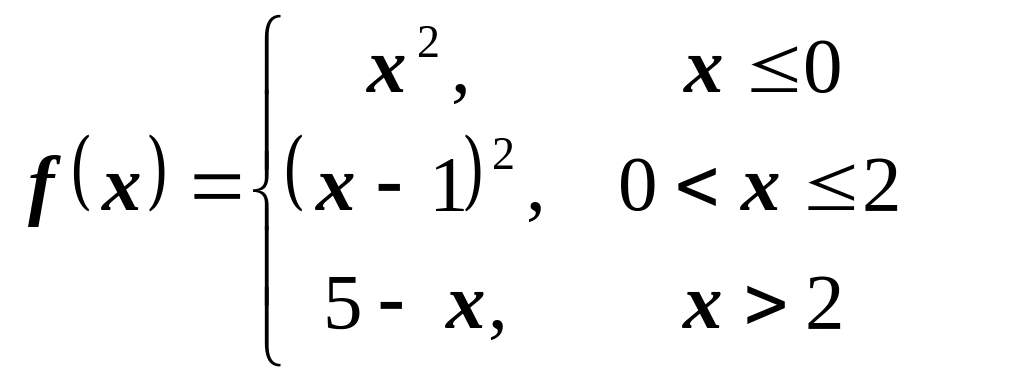
2)
![]() в т.
в т.
Вариант 30
1. Найти пределы функций
1)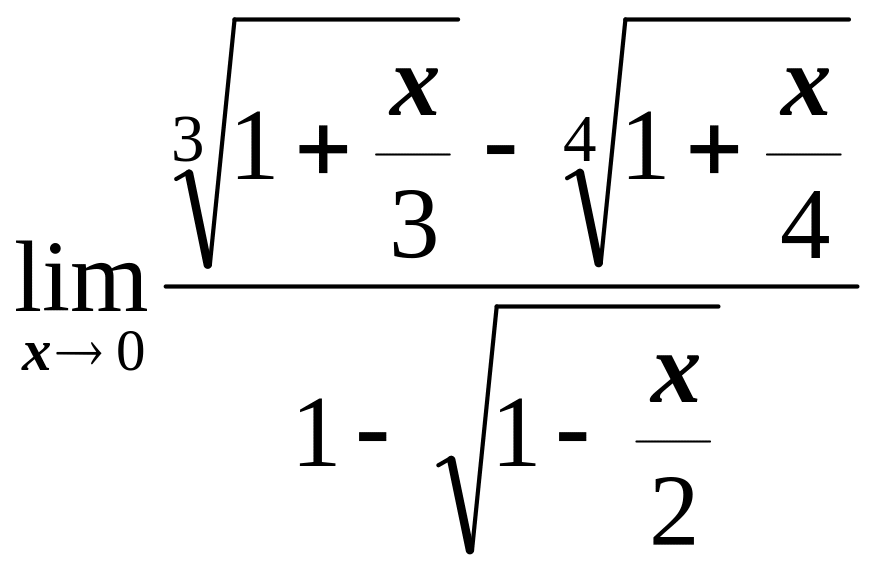 2)
2)![]() 3)
3)![]()
4)![]() 5)
5)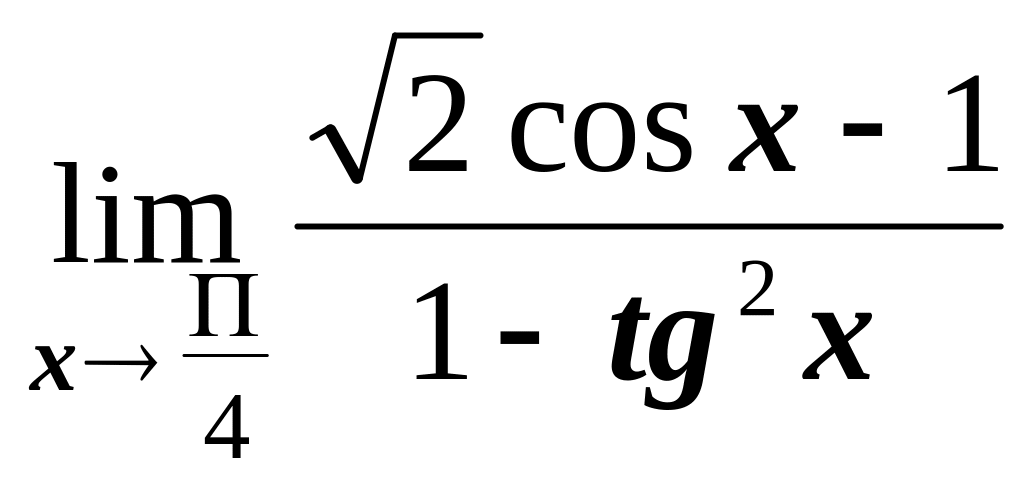
2. Исследовать на непрерывность и построить графики функций
1)![]() 2)
2)
Решение типового варианта
Найти
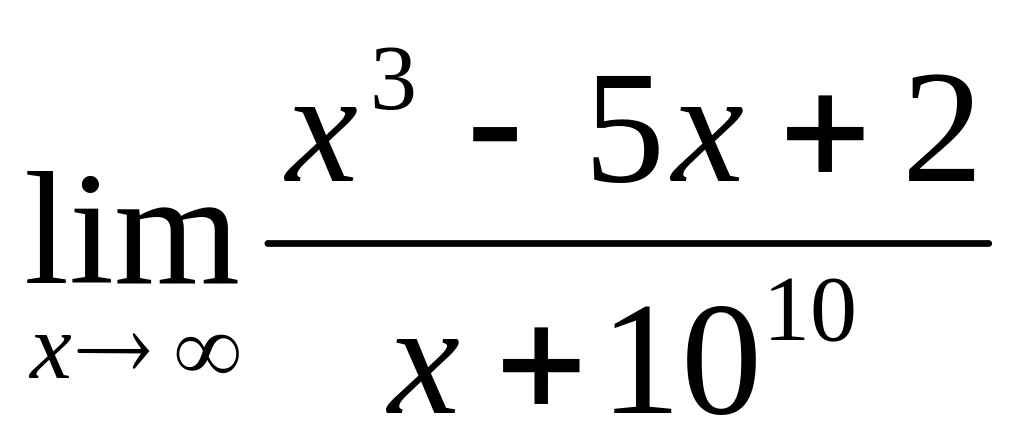
Решение.
При
![]() имеем неопределенность
имеем неопределенность
![]() .
Чтобы раскрыть эту неопределенность,
надо разделить числитель и знаменатель
дроби на наивысшую степень
.
Чтобы раскрыть эту неопределенность,
надо разделить числитель и знаменатель
дроби на наивысшую степень
![]() .
Получим
.
Получим
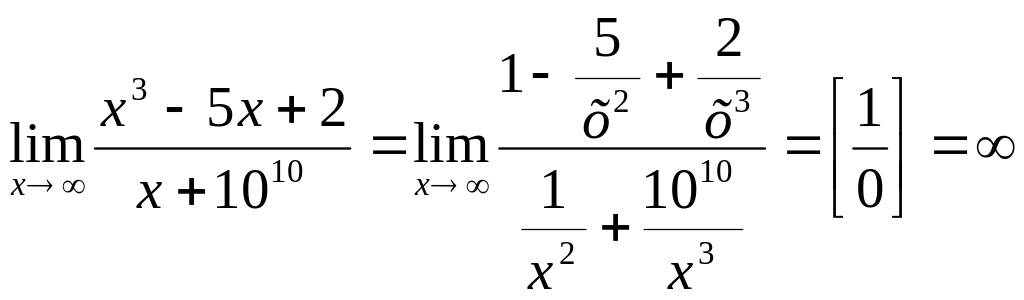 ,
т.к.
,
т.к.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Найти
 .
.
Решение.
При
![]() числитель и знаменатель дроби стремится
к нулю, т.е. мы имеем неопределенность
вида
числитель и знаменатель дроби стремится
к нулю, т.е. мы имеем неопределенность
вида
![]() .
Чтобы раскрыть эту неопределенность
избавимся от иррациональности в
знаменателе, умножив числитель и
знаменатель дроби на
.
Чтобы раскрыть эту неопределенность
избавимся от иррациональности в
знаменателе, умножив числитель и
знаменатель дроби на
![]() ,
числитель преобразуем по формуле
,
числитель преобразуем по формуле
![]() и воспользуемся известным пределом
и воспользуемся известным пределом
![]() .
Таким образом
.
Таким образом
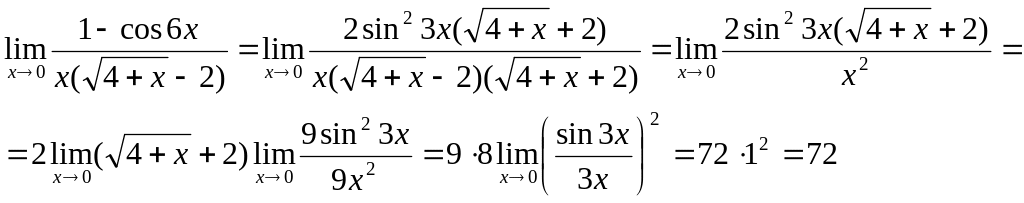
Найти
 .
.
Решение.
При
имеем неопределенность
.
Чтобы раскрыть эту неопределенность,
умножим числитель и знаменатель на
![]() ,
чтобы получить разность кубов в числителе.
Таким образом
,
чтобы получить разность кубов в числителе.
Таким образом
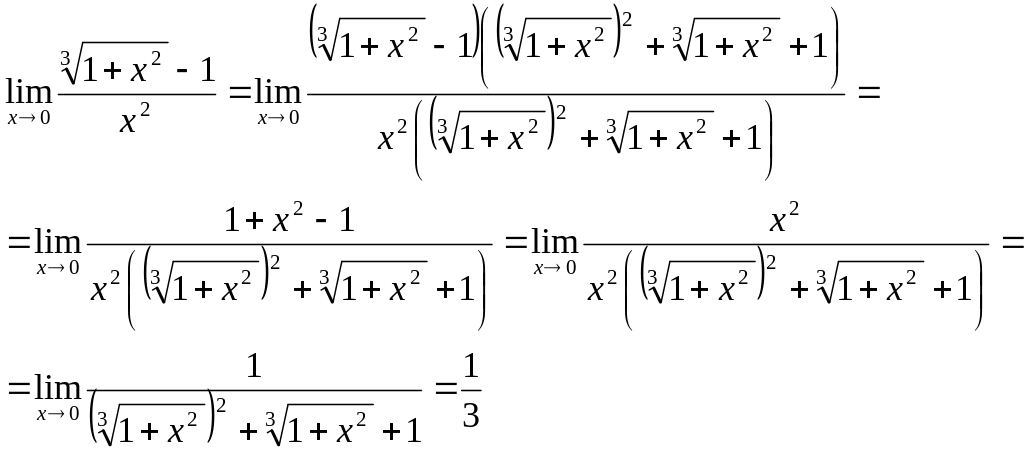
4. Найти
![]()
Решение.
При
![]() имеем неопределенность
.
Чтобы раскрыть эту неопределенность,
надо многочлены
имеем неопределенность
.
Чтобы раскрыть эту неопределенность,
надо многочлены
![]() и
и
![]() разделить на
разделить на
![]() (теорема
Безу). Таким образом:
(теорема
Безу). Таким образом:
![]()
5. Найти
![]()
Решение.
При
![]() имеем неопределенность
(предел основания равен 1). Чтобы раскрыть
эту неопределенность, надо основание
степени представить в виде
имеем неопределенность
(предел основания равен 1). Чтобы раскрыть
эту неопределенность, надо основание
степени представить в виде![]() ,
а в показателе выделяем множитель
,
а в показателе выделяем множитель
![]()

т.к.
![]() .
.
6. Исследовать на непрерывность и построить график функций:
![]()
Решение.
Функция
![]() неэлементарная, определена на всем
множестве действительных чисел, задана
тремя формулами на различных промежутках
изменения аргумента.
неэлементарная, определена на всем
множестве действительных чисел, задана
тремя формулами на различных промежутках
изменения аргумента.
Исследуем
непрерывность функции в точках
![]() и
.
Для этого вычислим односторонние пределы
при
и
.
Для этого вычислим односторонние пределы
при
![]() и
слева и справа. Получим
и
слева и справа. Получим
![]() ;
;
![]()
![]() .
.
Следовательно,
![]() ,
т.е.
,
т.е.
![]() непрерывна в точке
.
непрерывна в точке
.
![]() ;
;
![]() .
.
Таким образом, в точке функция имеет разрыв второго рода.
Построим график функции

Исследовать на непрерывность и найти точки разрыва функции:
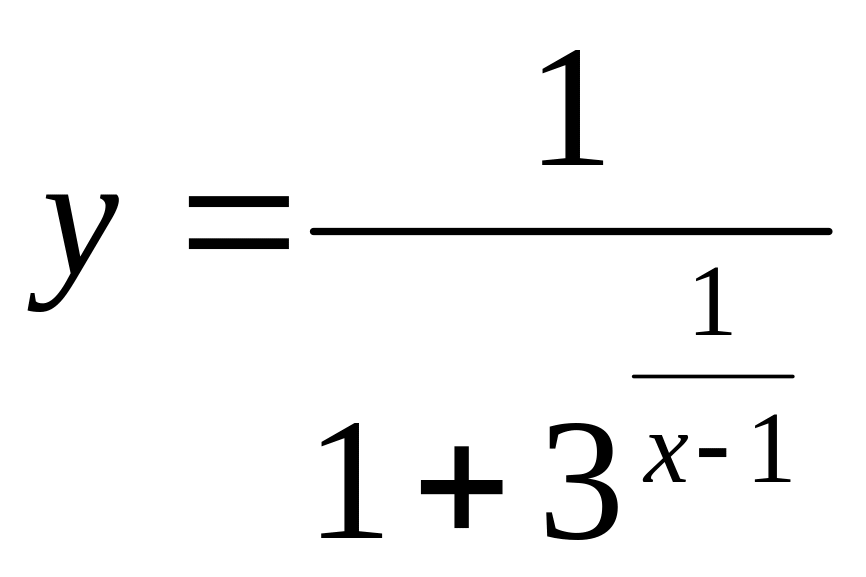 .
.
Решение.
Эту функцию можно представить как
сложную
![]() ,
где
,
где
![]() .
Знаменатель
первой
дроби нигде в нуль не обращается, поэтому
функция
непрерывна при любом значении u.
Функция
непрерывна для всех значений x,
кроме
.
Поэтому данная сложная функция непрерывна
для всех
.
Знаменатель
первой
дроби нигде в нуль не обращается, поэтому
функция
непрерывна при любом значении u.
Функция
непрерывна для всех значений x,
кроме
.
Поэтому данная сложная функция непрерывна
для всех
![]() .
Исследуем непрерывность функции в точке
.
Исследуем непрерывность функции в точке
![]() .
Вычислим односторонние пределы при
слева и справа. Получим
.
Вычислим односторонние пределы при
слева и справа. Получим
 .
.
 .
.
Таким образом, пределы справа и слева существуют, но не равны между собой, поэтому точка является точкой разрыва первого рода.
Скачок функции
![]() .
.

