3. Особенности применения метода.

Применение принципа максимума позволяет заменить вариационную задачу отыскания экстремума функционала качества J(x,u) по управлению u более простой задачей определения параметра u, обеспечивающего максимум функции H(u) (отсюда и название максимума).

При оптимальном управлении функции H(t) и 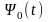постоянны во времени и 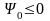, 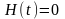. Решая задачу оптимального управления с использованием принципа максимума, прежде всего определяется максимум функции Гамильтона относительно управления u(t). Затем отыскивается оптимальное управление как функция от вспомогательной функции 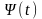. После этого выражение для управления u представляется в исходную и сопряженную системы дифференциальных уравнений для вычисления векторов x(t) и . Далее окончательно получают управление как функцию времени u(t).

Основная трудность этой вычислительной процедуры заключается в решении двухточечной краевой задачи, поскольку начальные условия для 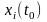заданы, а для 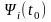 неизвестны. Это заставляет использовать известный практический прием проб и ошибок, который сводится к назначению и последующей коррекции совокупности начальных условий для .

В общем случае для нелинейных объектов принцип максимума дает только необходимые условия оптимальности, для линейных объектов эти условия являются и достаточными.

Условия трансверсальности. Пусть в задаче об оптимальном программном управлении начальное (6) и конечное (7) состояния не фиксированы (а t₀ и t₁ заданы) и могут перемещаться по поверхностям: левый конец траектории x_i(t) 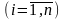по поверхности ν₀₁(x⁽⁰⁾, t₀)=0, а правый – по поверхности ν₁₁(x⁽¹⁾, t₁)=0.

Принцип максимума в этом случае в основном сохраняется (так как управление оптимальное при подвижных концах траектории x_i(t) , является оптимальным и в частном случае, когда концы закреплены), однако 2n граничных условий для системы (13), решения которых содержат 2n произвольных постоянных, определяются из условий трансверсальности:

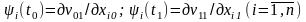. (14)

Если один из концов траектории x(t), например правый, закреплен, то граничные условия имеют вид 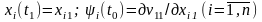. (15)

6. Принцип оптимальности. Функциональное уравнение метода динамического программирования. Особенности практического применения метода динамического программирования

Наряду с задачами оптимального управления в технике существуют задачи об оптимальном управлении в экономике, управлении войсками и т.д. (задачи об управлении запасами, ресурсами, составление расписаний, организация тыла). При этом обнаружилось, что процесс решения многих из них может быть представлен как некоторый многоплановый процесс принятия решений. Данная концепция получила название метода динамического программирования, что означает принятие решений во времени.

Основу метода динамического программирования, разработанного американским математиком Р. Беллманом, составляет принцип оптимальности, используя который выводят функциональное уравнение метода. Решение этого уравнения приводит к синтезу оптимального управления.